Синтез функциональных программ при помощи метода дедуктивных таблиц.

Содержание
Автоматический синтез программ
Дедуктивные таблицы
Свойства дедуктивных таблиц
Дедуктивные правила
Пример синтеза
Вспомогательные таблицы
Пример ввода вспомогательных таблиц
Заключение
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

Автоматический синтез программ
Предпосылки :
Увеличение сложности ПО
Увеличение требований к надежности ПО
Основные направления:
Дедуктивный синтез
Индуктивный синтез
Трансформационный синтез
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

Дедуктивные таблицы (1)
Один из методов дедуктивного синтеза.
Спецификация задается в виде формулы логики предикатов первого порядка
∀x ∃y Q[x,y]
где x – входная переменная,
y – выходная переменная,
Q – логическая формула, устанавливающая связь между входными и выходными переменными.
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

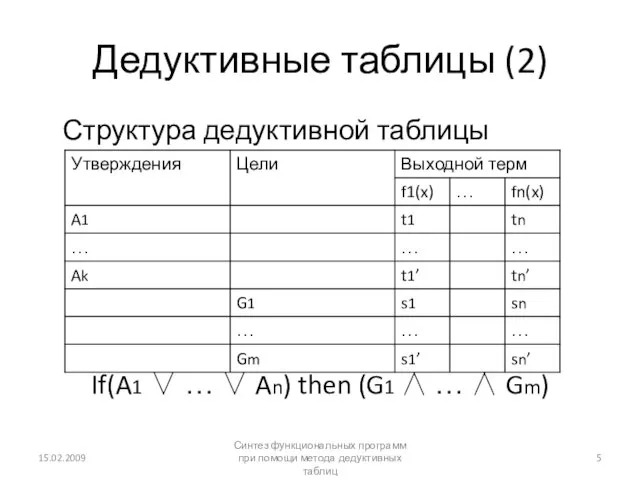
Дедуктивные таблицы (2)
Структура дедуктивной таблицы
If(A1 ∨ … ∨ An) then (G1 ∧ … ∧ Gm)
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

Дедуктивные таблицы (3)
Терм t, не содержащий свободных (на связанных с квантором) переменных, удовлетворяет строке таблицы
или
если для некоторой подстановки λ:
Утверждение Aλ не содержит свободных переменных и является ложным (Gλ – истинным)
Если строка имеет выходной терм s, то sλ не содержит свободных переменных и равен tλ.
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

Дедуктивные таблицы (4)
Доказательство в дедуктивной таблице проводиться до получения финальной строки
или
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

Свойства дедуктивных таблиц (1)
Двойственность
строка
эквивалентна строке
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

Свойства дедуктивных таблиц (2)
Переименование свободных переменных
π – перестановка
строка
эквивалентна строке
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

Свойства дедуктивных таблиц (3)
Добавление примера
λ – подстановка
Таблица
эквивалентна
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

Свойства дедуктивных таблиц (4)
Тождественные преобразования
Эквивалентность таблиц не нарушается при применении в строках тождественных преобразований на основе тождеств алгебры логики:
A ∧ A = A; A ∧ false = false;
A ∨ true = true; ¬ ¬ A = A;
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

Свойства дедуктивных таблиц (5)
Добавление и удаление тождественно истинного утверждения и тождественно ложной цели
Добавление и удаление свободной переменной
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

Дедуктивные правила (1)
Вычислимые термы – термы, не содержащие свободных переменных, которые можно получить на основе уже определенных констант, функций и предикатов.
Таблицы, для которых совпадают множества удовлетворяющих им вычислимых термов термов совпадают, называются подобными.
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

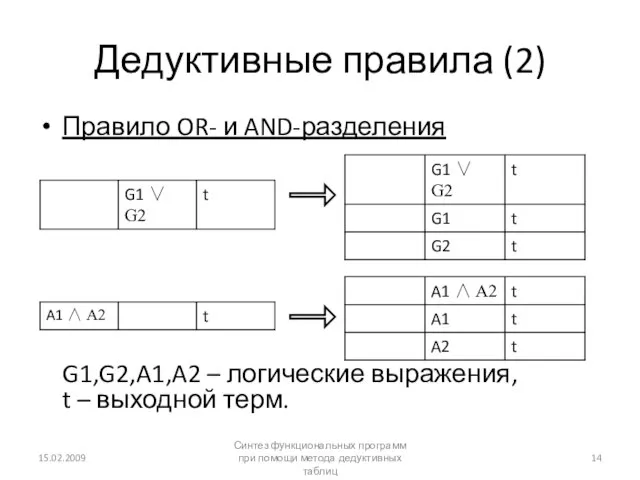
Дедуктивные правила (2)
Правило OR- и AND-разделения
G1,G2,A1,A2 – логические выражения, t – выходной терм.
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

Дедуктивные правила (3)
Правило резолюции
G1,G2 – логические выражения,
P, P’ – некоторые подвыражения G1 и G2,
λ – подстановка, для которой Pλ = P’λ,
s и t – выходные термы.
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

Дедуктивные правила (4)
Правило индукции.
wf-отношение – отношение, исключающее бесконечно убывающие цепочки.
Спецификация:
где a – входной параметр, z – выходная переменная, Q – логическая формула.
Гипотеза индукции:
где
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

Дедуктивные правила (5)
Правило замены эквивалентных термов
где G1, G2 – логические выражения,
[L=R] – подвыражение G1,
T – некоторый терм, входящий в G2, такой что для некоторой подстановки λ:Tλ = Lλ,
s и t – выходные термы.
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

Пример синтеза функциональной программы (1)
Спецификация:
z = fact(n) is
if n = 0 then z = 1 else z = n*fact(n-1)
В таблице
согласно тождеству
if A then B else C ≡ A ∧ B ∨ ¬A ∧ C
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

Пример синтеза функциональной программы (2)
OR-разделение
Резолюция. Общее подвыражение . (n=0).
Добавление примера{z1←1,z2 ← n*fact(n-1) }
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

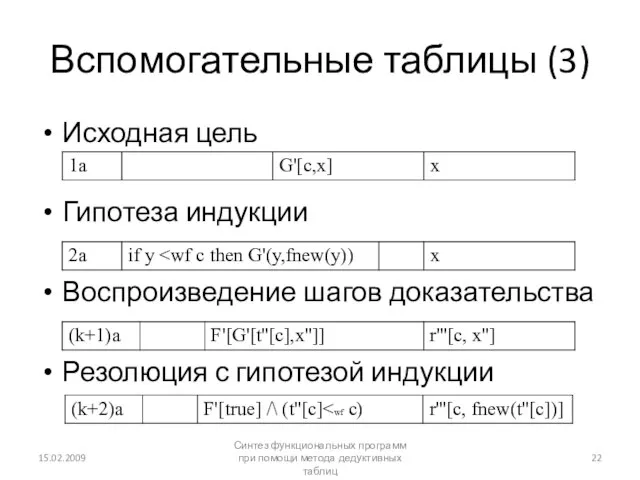
Вспомогательные таблицы (1)
Пусть в таблице присутствуют строки
где G, F – логические выражения, a – входной параметр, t[a], t’[a] – термы над входным параметром, x, x’ – выходные переменная, r[a,x], r’[a,x’] – выходные термы. F содержит реплику G.
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

Вспомогательные таблицы (2)
Если t’[a] вхождения t[a] на произвольную константу и построить обобщенную цель G’[c,x], которая станет исходной целью для вспомогательной таблицы (соответственно – спецификацией для вспомогательных функций).
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

Вспомогательные таблицы (3)
Исходная цель
Гипотеза индукции
Воспроизведение шагов доказательства
Резолюция с гипотезой индукции
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

Вспомогательные таблицы (4)
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц
Лемма
имеющаяся строка (i)
их резолюция завершает доказательство

Пример вывода вспомогательной таблицы (1)
Для функции сортировки списка чисел задается спецификация вида
z = sort(a) is perm(a,z) ∧ ord(z)
perm(x,y) – предикат, равный true, если его аргументы-списки есть перемтановки друг-друга.
ord(x) – предикат, равный true, если его аргумент-список упорядочен.
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

Пример вывода вспомогательной таблицы (2)
В ходе доказательства получается строка
Далее, строка
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

Исходная цель вспомогательной таблицы
Лемма
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц

Конец
15.02.2009
Синтез функциональных программ при помощи метода дедуктивных таблиц