Содержание
- 2. Цели урока: Ввести понятие перпендикуляра к прямой, медианы, биссектрисы и высоты треугольника. Доказать теорему о перпендикуляре
- 3. Ход урока. огр. момент Проверка домашнего задания. Повторение. Анализ самостоятельной работы. Изучение нового материала.
- 4. Практическое задание Начертите прямую а и отметьте точку А, не лежащую на прямой
- 5. Практическое задание Через точку А проведите прямую, перпендикулярную прямой а. Точку пересечения обозначьте Н.
- 6. Отрезок АН – перпендикуляр, проведённый из точки А к прямой а, если: АН ⊥ a A
- 7. Дано: а – прямая, A О a Доказать: из точки А к прямой а можно провести
- 8. Практическое задание Постройте треугольник АВС, соедините вершину А с серединой противолежащей стороны М
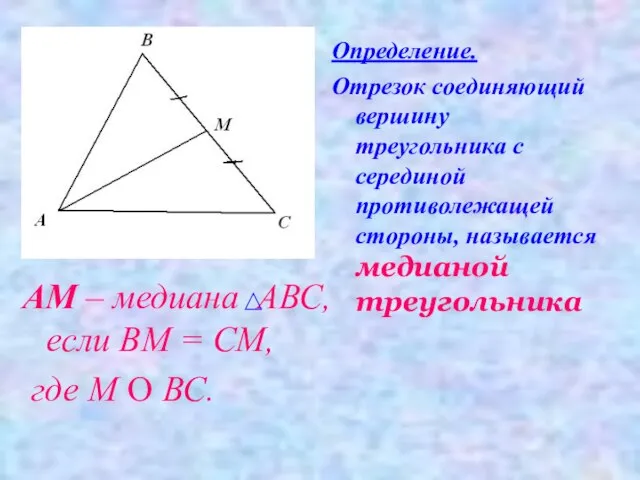
- 9. АМ – медиана АВС, если ВМ = СМ, где М О ВС. Определение. Отрезок соединяющий вершину
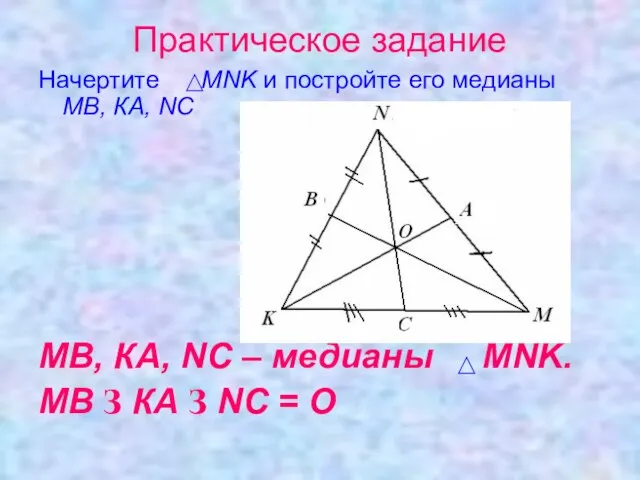
- 10. Практическое задание Начертите MNK и постройте его медианы МВ, КА, NС МВ, КА, NС – медианы
- 11. Практическое задание Постройте треугольник АВС, Проведите биссектрису угла В, точку пересечения биссектрисы с противолежащей стороны обозначьте
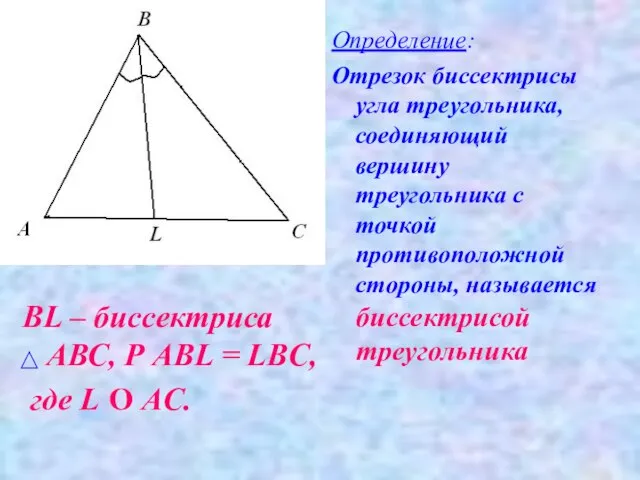
- 12. BL – биссектриса АВС, Р AВL = LBС, где L О AС. Определение: Отрезок биссектрисы угла
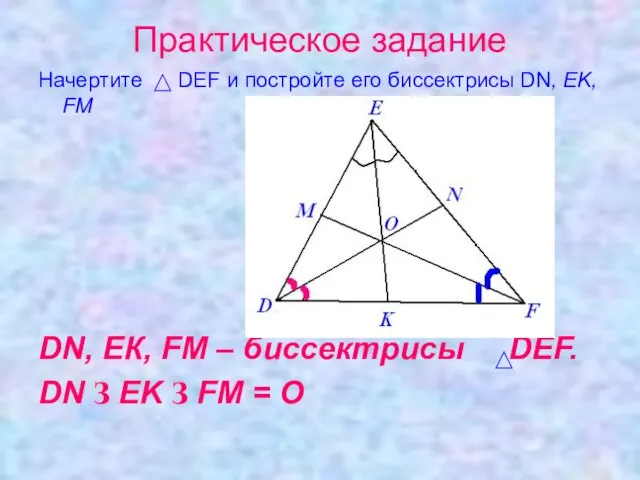
- 13. Практическое задание Начертите DEF и постройте его биссектрисы DN, EK, FM DN, EК, FM – биссектрисы
- 14. Практическое задание Постройте треугольник АВС, Проведите перпендикуляр АН из точки А к стороне ВС.
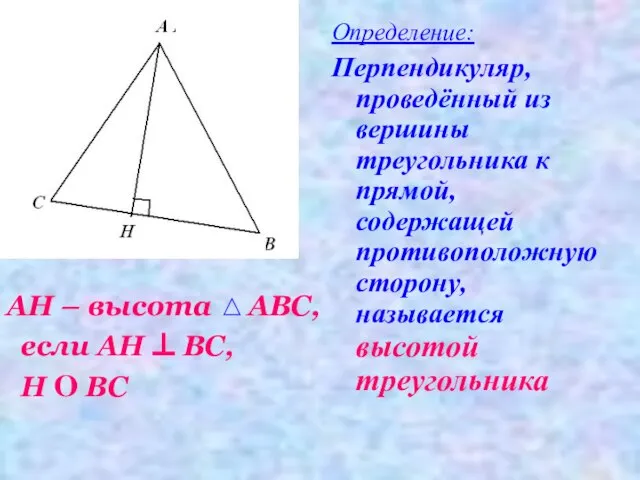
- 15. АН – высота АВС, если АН ⊥ ВС, Н О ВС Определение: Перпендикуляр, проведённый из вершины
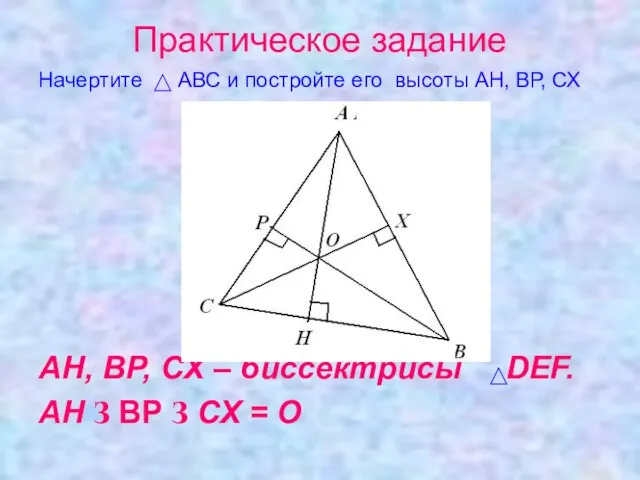
- 16. Практическое задание Начертите АВС и постройте его высоты АН, ВР, СХ АН, ВР, СХ – биссектрисы
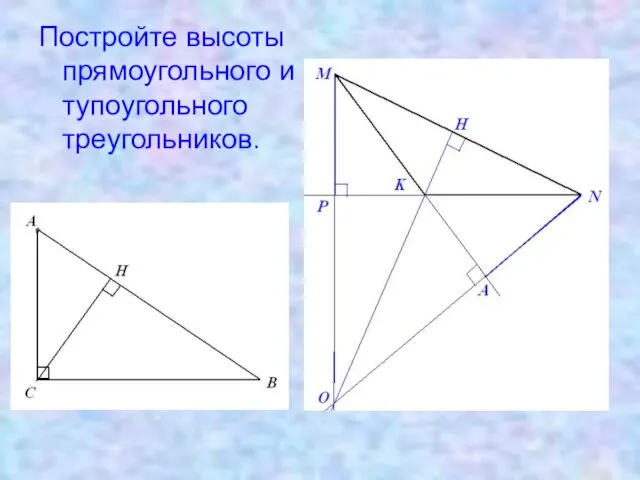
- 17. Постройте высоты прямоугольного и тупоугольного треугольников.
- 18. Решение задач Устно решите № 60 (а) № 63 из рабочей тетради
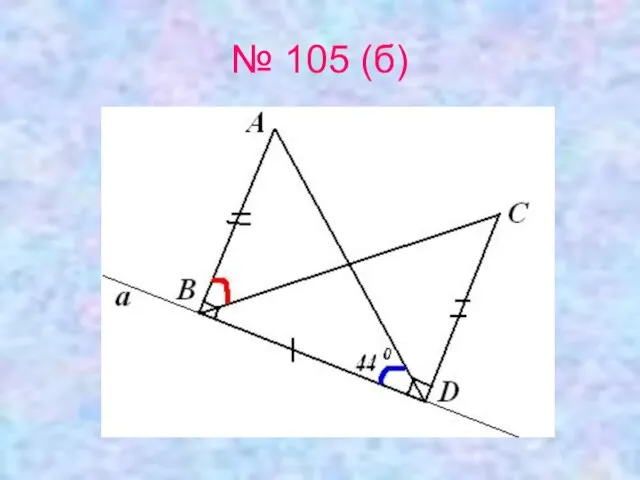
- 19. Письменно решите № 105 (б)
- 20. № 105 (б)
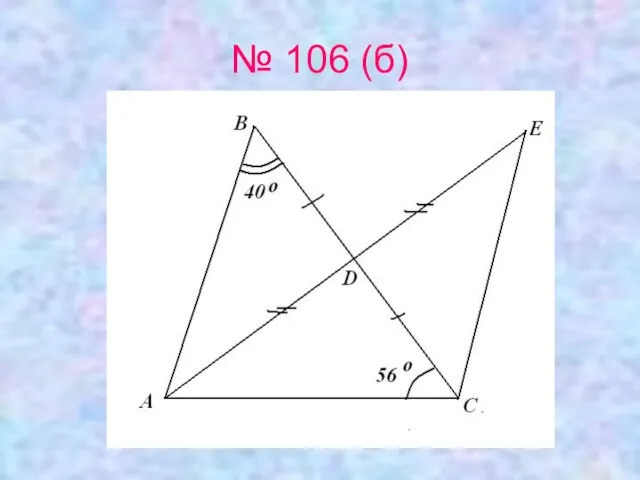
- 21. № 106 (б)
- 23. Скачать презентацию











 Windows 95
Windows 95 Презентация на тему Сложение дробей с одинаковыми знаменателями (4 класс)
Презентация на тему Сложение дробей с одинаковыми знаменателями (4 класс)  ДНЕВНИКИ
ДНЕВНИКИ Презентация на тему Наступление советских войск под Ленинградом
Презентация на тему Наступление советских войск под Ленинградом  Презентация учителя для выявления представлений и интересов учащихся Проект Дистанционное образование в школе
Презентация учителя для выявления представлений и интересов учащихся Проект Дистанционное образование в школе Больше.Меньше
Больше.Меньше Государственное управление развитием спортивной науки
Государственное управление развитием спортивной науки Стресс. Влияние стресса на здоровье
Стресс. Влияние стресса на здоровье Образы деревьев. Украшение и фантазия. Украшения для королевы осени
Образы деревьев. Украшение и фантазия. Украшения для королевы осени Презентация на тему Наполеоновская империя
Презентация на тему Наполеоновская империя  Макаронные изделия. Виды макаронных изделий
Макаронные изделия. Виды макаронных изделий Между Раем и Адом. Милостивый блудник на иконах Страшного Суда
Между Раем и Адом. Милостивый блудник на иконах Страшного Суда Экономика
Экономика Строение и свойства РНК
Строение и свойства РНК Мутации и отбор
Мутации и отбор Музеи
Музеи Тема урока: "Причастие и деепричастие. Орфография и пунктуация".
Тема урока: "Причастие и деепричастие. Орфография и пунктуация". Балансовое обобщение и его роль в бухгалтерском учете. Тема 3
Балансовое обобщение и его роль в бухгалтерском учете. Тема 3 Игра жизни - Аватар
Игра жизни - Аватар Московский финансово - юридический университет МФЮА
Московский финансово - юридический университет МФЮА ПРОДАЖА НЕЖИЛОГО ПОМЕЩЕНИЯ
ПРОДАЖА НЕЖИЛОГО ПОМЕЩЕНИЯ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ ФІЗИЧНОГО ВИХОВАННЯ І СПОРТУ УКРАЇНИ
НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ ФІЗИЧНОГО ВИХОВАННЯ І СПОРТУ УКРАЇНИ Программа восстановления экономического роста Вологодской области
Программа восстановления экономического роста Вологодской области Коммуникативное взаимодействие пресс-служб различных уровней власти на примере освещения мероприятий Года Учителя Смолина Юли
Коммуникативное взаимодействие пресс-служб различных уровней власти на примере освещения мероприятий Года Учителя Смолина Юли Технология EPM (Encrypted Parts Marking) для шифрованного маркирования, применяемая для защиты документов и продуктов (основан на семи принцип
Технология EPM (Encrypted Parts Marking) для шифрованного маркирования, применяемая для защиты документов и продуктов (основан на семи принцип a set of activities for essay writing
a set of activities for essay writing PATTERNS OF ENGLISH
PATTERNS OF ENGLISH Постановка проблемы и методологический аппарат исследования в образовании. (Лекция 3)
Постановка проблемы и методологический аппарат исследования в образовании. (Лекция 3)