Методы оптимизации

Под оптимизацией понимают
процесс выбора наилучшего варианта
из всех возможных
В процессе решения задачи оптимизации
обычно необходимо найти оптимальные значения
некоторых параметров, определяющих данную задачу.
При решении инженерных задач их принято называть
проектными параметрами,
а в экономических задачах их обычно называют
параметрами плана.

Выбор оптимального решения или
сравнение двух альтернативных решений
проводится с помощью
некоторой зависимой величины (функции),
определяемой проектными параметрами.
Эта величина называется целевой функцией
(или критерием качества).
В процессе решения задачи оптимизации
должны быть найдены такие значения
проектных параметров, при которых
целевая функция имеет минимум (или максимум).

Задачи оптимизации.
Безусловная задача оптимизации состоит в отыскании максимума или минимума действительной функции от n действительных переменных и определении соответствующих значений аргументов
Условные задачи оптимизации, или задачи с ограничениями, — это такие, при формулировке которых задаются некоторые условия (ограничения) на множестве.

Теория и методы решения задач оптимизации
при наличии ограничений
составляют предмет исследования одного из важных разделов прикладной математики —
математического программирования.

§ 2. Одномерная оптимизация
Одномерная задача оптимизации в общем случае
формулируется следующим образом: Найти наименьшее (или наибольшее)
значение целевой функции у = f(x),
заданной на множестве
и определить значение проектного параметра
при котором целевая функция принимает
экстремальное значение.
Существование решения поставленной задачи
вытекает из следующей теоремы:

Теорема Вейерштрасса.
Всякая функция f(x), непрерывная на отрезке
принимает на этом отрезке наименьшее и наибольшее
значения, т. е. на отрезке
существуют такие точки
и
что для любого
имеют место неравенства
.

Методы поиска.
Будем предполагать, что целевая функция
унимодальна,
т. е. на данном отрезке она имеет только один минимум.
Численные методы поиска экстремальных значений
функции рассмотрим на примере нахождения
минимума функции f(x) на отрезке

Погрешность приближенного решения задачи определяется
разностью между оптимальным значением х
проектного параметра и приближением к нему
Потребуем, чтобы эта погрешность была
по модулю меньше заданного допустимого значения

Процесс решения задачи методом поиска
состоит в последовательном сужении
интервала изменения проектного параметра,
называемого интервалом неопределенности
В начале процесса оптимизации его длина равна b – a,
а к концу она должна стать меньше
т. е. оптимальное значение проектного параметра
должно находиться в интервале неопределенности —
отрезке
причем

Тогда для выполнения условия
в качестве приближения к оптимальному значению
можно принять любое
Например,
или
, или
В последнем случае достаточно выполнения неравенства

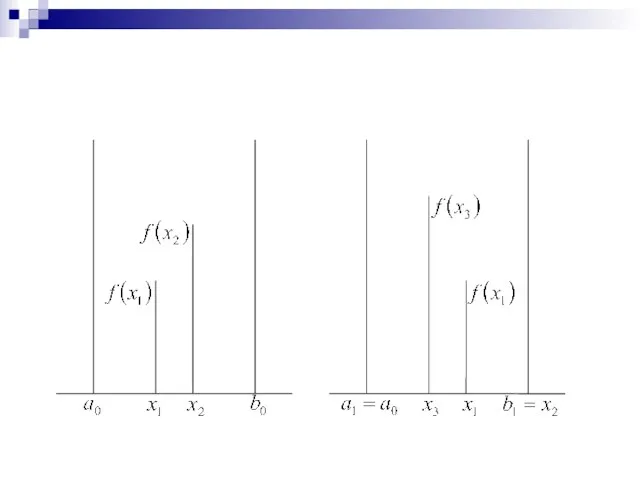
Метод золотого сечения.
Метод состоит в построении
последовательности отрезков
,
,…, стягивающихся к точке минимума
функции f(x).
На каждом шаге, за исключением первого,
вычисление значения функции f(x)
проводится лишь в одной точке.
Эта точка, называемая золотым сечением,
выбирается специальным образом.

1 шаг
внутри отрезка
выбираем некоторые внутренние точки
и
и вычисляем значения целевой функции
и

Поскольку в данном случае
<
очевидно, что минимум расположен
на одном из прилегающих к
отрезков:
или
Поэтому отрезок
можно отбросить, сузив тем самым
первоначальный интервал неопределенности.

Второй шаг
проводим на отрезке
где
Нужно снова выбрать две внутренние точки,
но одна из них
осталась из предыдущего шага,
поэтому достаточно выбрать лишь одну точку
вычислить значение
и провести сравнение.

Поскольку здесь
<
ясно, что минимум находится на отрезке
Обозначим этот отрезок
снова выберем одну внутреннюю точку
и повторим процедуру сужения
интервала неопределенности.
Процесс оптимизации повторяется до тех пор,
пока длина очередного отрезка
не станет меньше заданной величины

Теперь рассмотрим способ размещения внутренних точек
на каждом отрезке
Пусть длина интервала неопределенности равна l,
а точка деления разбивает его на части
,
>
Золотое сечение интервала неопределенности
выбирается так, чтобы отношение длины
большего отрезка к длине всего интервала
равнялось отношению длины меньшего отрезка
к длине большего отрезка:

Из этого соотношения можно найти точку деления,
вычислив отношения
Преобразуем выражение и найдем значения
и

Поскольку нас интересует только положительное решение, то
Очевидно, что интервал неопределенности можно
разделить в соотношении золотого сечения двояко:
в пропорциях
:
и
:
В данном случае имеем
Аналогично,

Начальная длина интервала неопределенности составляет
После первого шага оптимизации получается
новый интервал неопределенности — отрезок
Его длина равна

На втором шаге отрезок
также делится в соотношении золотого сечения.
При этом одной из точек деления будет точка
Покажем это:
Последнее равенство следует из соотношения

Вторая точка деления
выбирается так же, как выбирается точка
при делении отрезка
т. е.
И снова интервал неопределенности
уменьшается до размера

По аналогии можно записать координаты
точек деления у и z отрезка на к-м шаге оптимизации (у < z):

Вычислению, естественно,
подлежит только одна из координат у, z
другая координата берется с предыдущего шага.
При этом длина интервала неопределенности равна