Методы решений заданий С5. Метод областей в решении задач

(«переход» метода интервалов с прямой на плоскость)
1. Область определения
2. Граничные линии
3. Координатная плоскость
4. Знаки в областях
5.Ответ по рисунку.
1. Область определения
2. Корни
3. Ось
4. Знаки на интервалах
5. Ответ.
Метод интервалов:
Метод областей:
Обобщённый метод областей

Решение. На координатной плоскости нарисуем линии, определяемые равенствами
х – у = 0 (у = х) и
х⋅ у - 1= 0 (у = 1/х), которые
разбивают плоскость на 6 областей.
При х = 1, у = 0 левая часть неравенства равна -1(отрицательна)
Ответ: заштрихованные области на рисунке удовлетворяют условию (х – у) (х у –1) ≥ 0
х
у
0
1
- 1
- 1
1
На координатной плоскости изобразите множество точек , координаты которых удовлетворяют неравенству(х – у) (х у –1) ≥ 0
1
2
3
4
5
6
Следовательно, в 1 области, содержащей точку (1; 0), левая часть неравенства имеет знак минус, а в остальных областях её знаки чередуются.
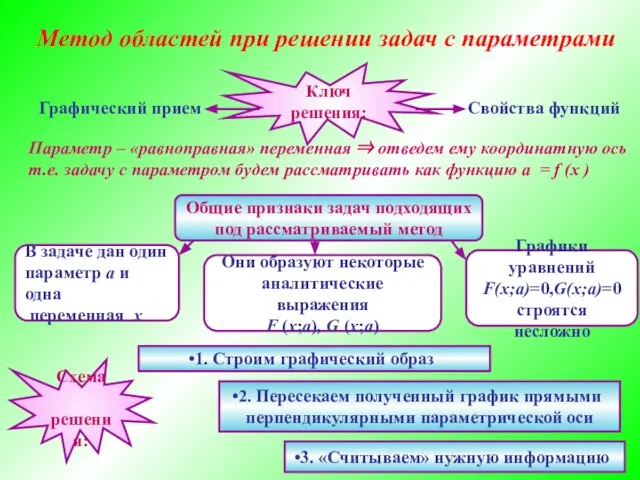
Пример для понимания «метода областей»

Граничные линии:
Они разбивают плоскость на 8 областей
- 1
- 1
1
1
х
у
0
На координатной плоскости изобразите множество точек, удовлетворяющих неравенству
Ответ: заштрихованные области
на рисунке.
Область определения неравенства:
Проводим граничные линии, с учётом области определения
Определяем знаки на областях подстановкой в отдельных точках
Пример для понимания «метода областей»

Метод областей при решении задач с параметрами
Ключ решения:
Графический прием
Свойства функций
Параметр – «равноправная» переменная ⇒ отведем ему координатную ось т.е. задачу с параметром будем рассматривать как функцию a = f (x )
Общие признаки задач подходящих
под рассматриваемый метод
В задаче дан один
параметр а и одна
переменная х
Они образуют некоторые
аналитические выражения
F (x;a), G (x;a)
Графики уравнений
F(x;a)=0,G(x;a)=0
строятся несложно
1. Строим графический образ
2. Пересекаем полученный график прямыми
перпендикулярными параметрической оси
3. «Считываем» нужную информацию
Схема
решения:

Найти все значения параметра р, при каждом из которых
множество решений неравенства (р – х 2 )(р + х – 2) < 0 не содержит ни одного решения неравенства х 2 ≤ 1
.
Применим обобщенный метод областей.
2) Определим знаки в полученных пяти областях, и укажем решение данного неравенства.
3) Осталось из полученного множества
исключить решения неравенства х 2 ≤ 1
По рисунку легко считываем ответ
Ответ: р ≤ 0, р ≥ 3
1) Построим граничные линии
р = 3
р = 0
0
2
2
-1
1
3
1
р = х 2 и р = 2 - х
При р ≤ 0, р ≥ 3 в решениях исходного неравенства нет решений неравенства х 2 ≤ 1.
1
2
3
4
5
│x│≤ 1, - 1 < x < 1

Сколько решений имеет система
в зависимости от параметра а?
2
-2
2
-2
1
-1
1
Графиком второго уравнения является неподвижная окружность с центром в начале координат и радиусом 1
4 решения при а = 1
Ответ:
решений нет, если
8 решений, если
4 решения, если
0

При каких положительных значениях параметра а, система уравнений имеет ровно четыре решения? и симметрично отображаем относительно оси абсцисс.
Второе уравнение задает семейство окружностей с центром (2;0) и радиусом а.
0

Решение. Рассмотрим сумму данных выражений
t
у
0
5
12
Сумма данного выражения равна 1, при пересечении параболы с горизонтальной прямой . По рисунку «считываем» ответ:
5 ≤ а ≤ 12
Пусть сos 2 x + 1= t; t ϵ [1; 2];
тогда уравнение примет вид
При каких значениях параметра а сумма log a (cos 2 x + 1) и log a (cos 2 x + 5) равна 1 хотя бы при одном значении х?
log a (cos 2 x + 1) + log a (cos 2 x + 5) = 1;
заметим, 0 ≤ cos 2 x ≤ 1
log a (t∙(t + 4)) = 1; откуда
t 2 + 4t = a
у = а
у = а
Ответ: при всех a ∈ [5;12]

Построим эскизы этих линий и определим из рисунка количество их общих точек.
х
у
2
-2
3
3
1
5
А
В
С
О
Найдите все значения параметра а, при которых количество
корней уравнения (5 - а) х 3 – 4 х 2 + х = 0 равно количеству
общих точек линий х 2 + у 2 = а 2 и у = 5 - │х - 1│