Содержание
- 2. Логика - наука, изучающая законы и формы мышления
- 3. Кодификатор (ФК) 1.3 Основы логики 1.3.1 Алгебра логики. 1.3.2 Логические выражения и их преобразование. 1.3.3 Построение
- 4. Устные задачи 1. Какое из следующих предложений является высказыванием? Ура, скоро Новый Год! Светает. 3+4*56. Первый
- 5. 3. Из предложенных высказываний выберите логическую сумму. Хорошо, когда утро начинается с зарядки и обливания холодной
- 6. МЕТОДЫ РЕШЕНИЯ ЛОГИЧЕСКИХ ЗАДАЧ Табличный метод Метод графов Решение с помощью алгебры высказываний
- 7. Табличный метод Задача 1: Встретились 3 друга: скульптор Белов, скрипач Чернов и художник Рыжов. «Замечательно, что
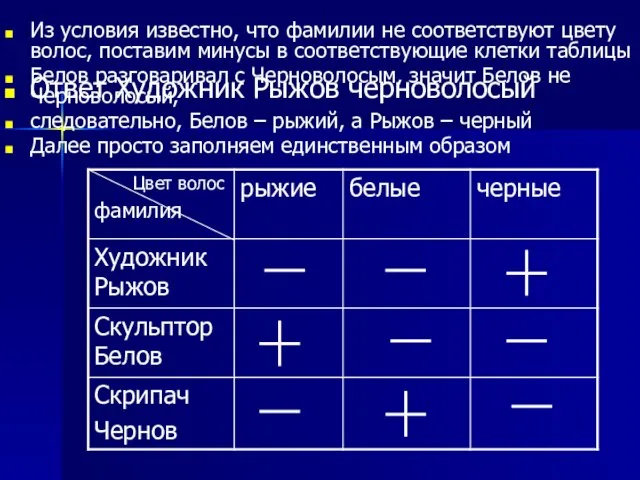
- 8. Из условия известно, что фамилии не соответствуют цвету волос, поставим минусы в соответствующие клетки таблицы Белов
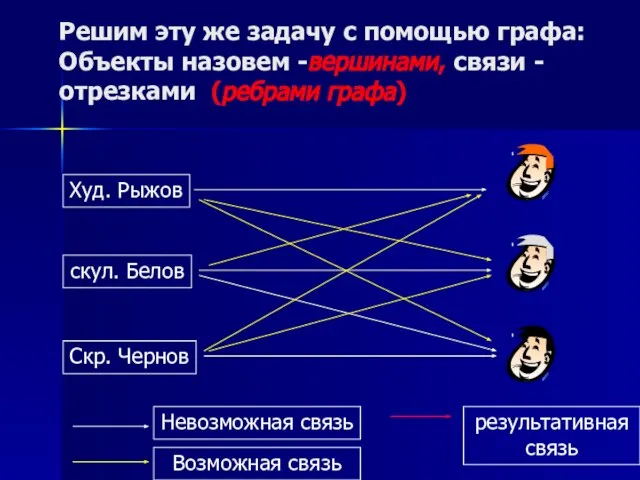
- 9. Решим эту же задачу с помощью графа: Объекты назовем -вершинами, связи - отрезками (ребрами графа) Скр.
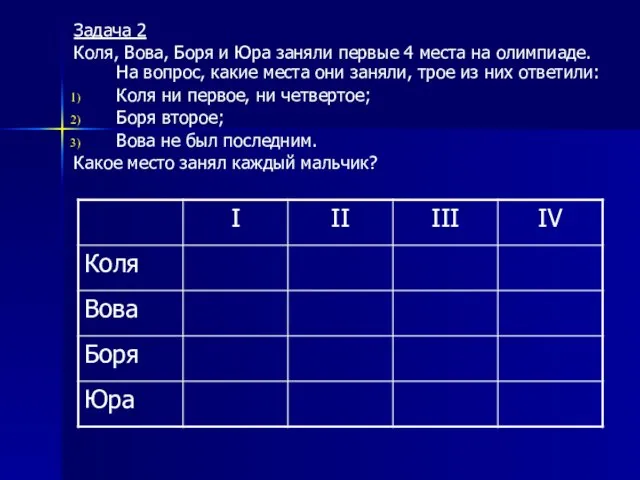
- 10. Задача 2 Коля, Вова, Боря и Юра заняли первые 4 места на олимпиаде. На вопрос, какие
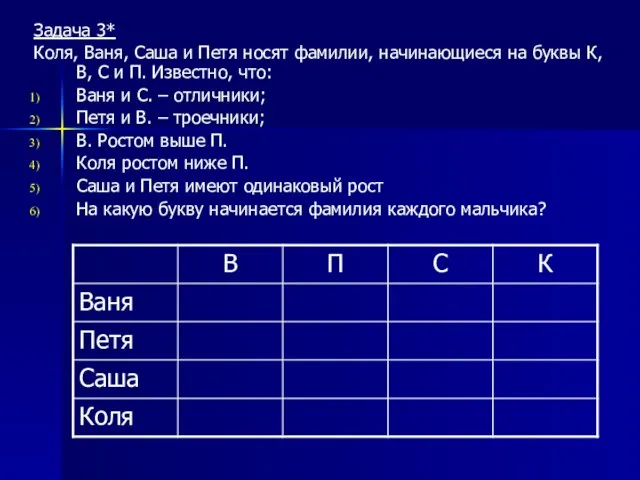
- 11. Задача 3* Коля, Ваня, Саша и Петя носят фамилии, начинающиеся на буквы К, В, С и
- 12. Задача 4: В лесу проводился кросс. Обсуждая его итоги, 1 белка сказала: «Первое место у зайца,
- 13. РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ внимательно изучить условие; выделить простые высказывания и обозначить их латинскими буквами; записать условие
- 14. Решение с помощью алгебры высказываний задачи 4: В лесу проводился кросс. Обсуждая его итоги, 1 белка
- 15. Задача 6. Виктор, Роман, Леонид и Сергей заняли на математической олимпиаде четыре первых места. Когда их
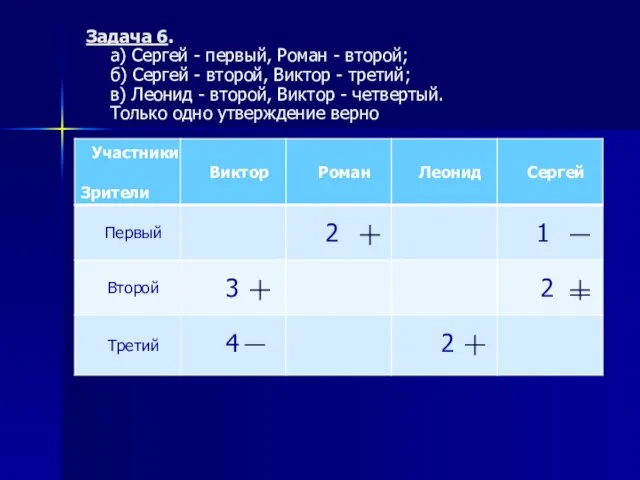
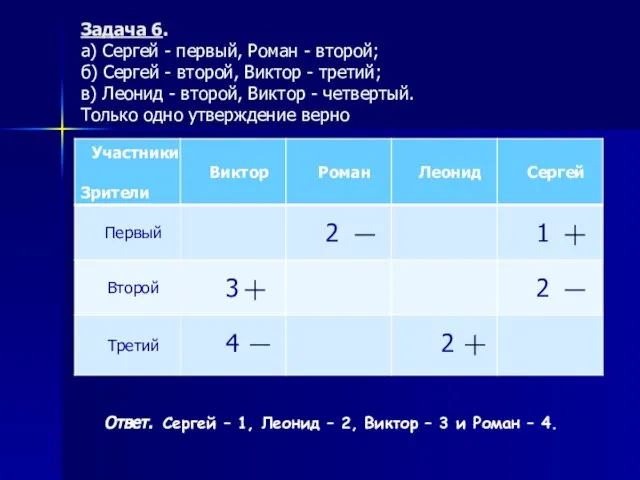
- 16. Задача 6. а) Сергей - первый, Роман - второй; б) Сергей - второй, Виктор - третий;
- 17. Задача 6. а) Сергей - первый, Роман - второй; б) Сергей - второй, Виктор - третий;
- 18. Задача 7. а) «если не будет ветра, то будет пасмурная погода без дождя»; б) «если будет
- 20. Скачать презентацию











 Принципы, цели и методы государственного регулирования экономики
Принципы, цели и методы государственного регулирования экономики Товарная политика
Товарная политика Егэ орфоэпия
Егэ орфоэпия Снегопад Новогодних предложений 2009-2010
Снегопад Новогодних предложений 2009-2010 Как-то компания литераторов отправилась в пригородный ресторан. Писатель А.И.Куприн посмотрел меню и заказал: - Нам десять порций
Как-то компания литераторов отправилась в пригородный ресторан. Писатель А.И.Куприн посмотрел меню и заказал: - Нам десять порций  Электродвигатели. История создания электродвигателя
Электродвигатели. История создания электродвигателя Лыжи. Лыжные классические хода. Применение этих ходов на дистанции, пересеченной местности
Лыжи. Лыжные классические хода. Применение этих ходов на дистанции, пересеченной местности Что такое хорошо и что такое плохо ?
Что такое хорошо и что такое плохо ? Дорога к трем п: понимание, прозрачность, повышение эффективности
Дорога к трем п: понимание, прозрачность, повышение эффективности Методический совет
Методический совет Вредны ли компьютерные игры
Вредны ли компьютерные игры Презентация на тему Греко-персидские войны. Платейское сражение
Презентация на тему Греко-персидские войны. Платейское сражение «Решение арифметических задач».
«Решение арифметических задач». Презентация на тему Поляризация света
Презентация на тему Поляризация света Презентация на тему Десятичные дроби (5 класс)
Презентация на тему Десятичные дроби (5 класс) Фонетика. Графика (9 класс)
Фонетика. Графика (9 класс) Распространение волн в нелинейной среде
Распространение волн в нелинейной среде Презентация на тему Орфографическая работа по русскому языку в 6 классе
Презентация на тему Орфографическая работа по русскому языку в 6 классе эмо
эмо «Солнечный городок»
«Солнечный городок» Мой дом — мой образ жизни
Мой дом — мой образ жизни Corporation Johnson & Johnson
Corporation Johnson & Johnson Курить или не курить?
Курить или не курить? Роль регионального модельного центра и муниципальных опорных центров (РМЦ и МОЦ) в жизни человека
Роль регионального модельного центра и муниципальных опорных центров (РМЦ и МОЦ) в жизни человека Новый Лингвистический и Экзегетический Ключ к греческому тексту Нового Завета
Новый Лингвистический и Экзегетический Ключ к греческому тексту Нового Завета Алгоритм решения простых задач
Алгоритм решения простых задач Что такое калибровка?
Что такое калибровка?