Метрические задачи

Метрические задачи-это задачи на определение расстояний ,углов и истинных величин плоских фигур

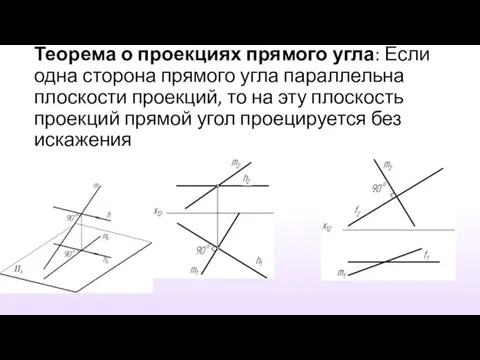
Теорема о проекциях прямого угла: Если одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость проекций прямой угол проецируется без искажения

Перпендикулярность прямой и плоскости
Из геометрии известно, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости .В начертательной геометрии для того чтобы прямой угол проецировался в истинную величину надо фронтальную проекцию перпендикуляра провести перпендикулярно фронтальной проекции фронтали n2┴f2, а горизонтальную проекцию перпендикуляра перпендикулярно горизонтальной проекции горизонтали n1┴h1

Пример 1. В точке А провести перпендикуляр к плоскости α(ΔАВС)
Прямая АВ является фронталью, а прямая АС - горизонталью. Строим p2⊥А2В2 и p1⊥А1С1.

Пример 2.Провести перпендикуляр к плоскости α(а║в)
1.Строим горизонталь и фронталь через точку К.
2.Строим n2⊥f2; n1 ⊥h 1

Способы преобразования проекций применяют для получения нового изображения объекта или группы объектов, которое позволяет упростить решение поставленной задачи.
Как правило, это переход от общего положения к частному.

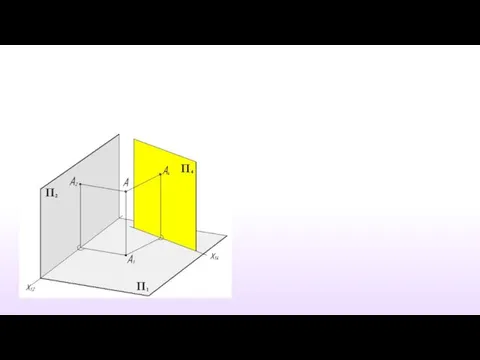
Дополнительное прямоугольное проецирование

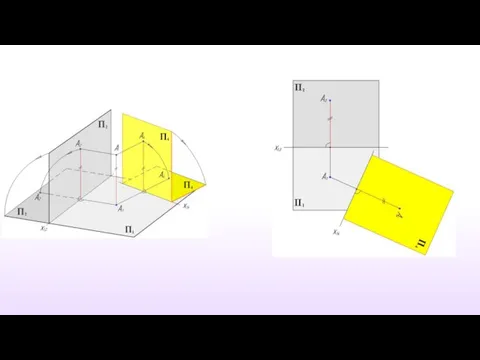
Вновь вводимая плоскость проекций должна быть перпендикулярна либо плоскости проекций П2, либо П1.
П4⊥ П1
П1∩ П4= х14

Пример1. Найти длину отрезка АВ.
П4 ⊥ ‖АВ и П4⊥П1

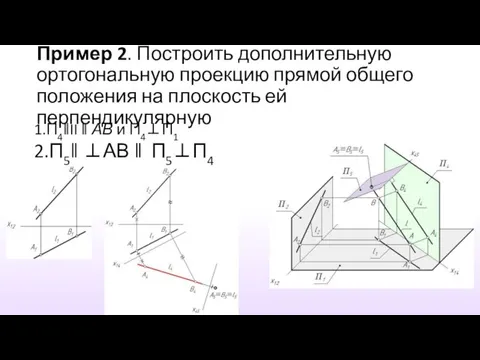
Пример 2. Построить дополнительную ортогональную проекцию прямой общего положения на плоскость ей перпендикулярную
1.П4‖II ‖ АВ и П4⊥П1
2.П5‖ ⊥АВ ‖ П5⊥П4

П4⊥П1 и П4 ║АК
Пример 3. Определить расстояние от точки А до прямой h.

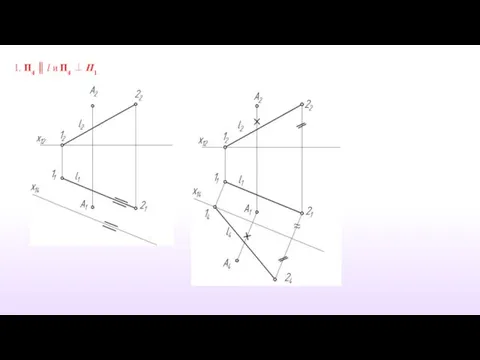
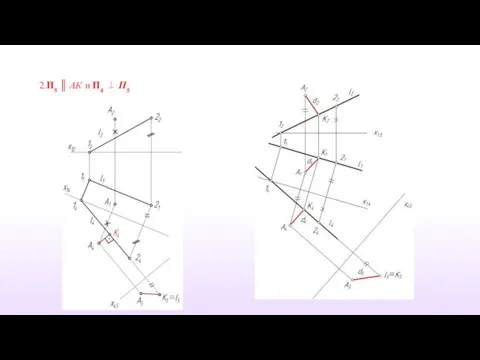
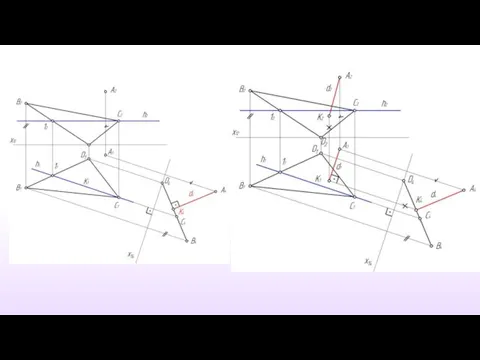
Пример 4. Определить расстояние от точки А до прямой l.

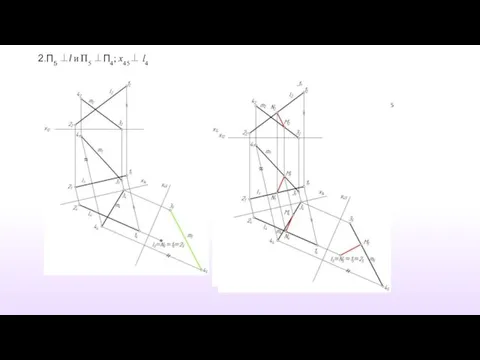
1. П4 ║ l и П4 ⊥ П1

2.П5 ║ АК и П4 ⊥ П5

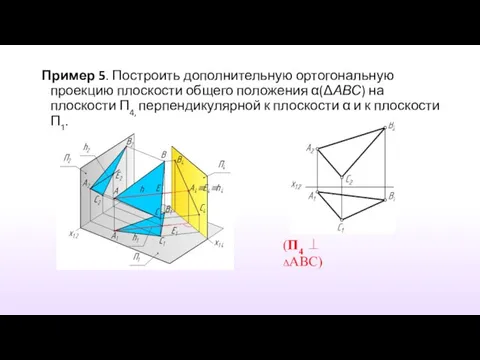
Пример 5. Построить дополнительную ортогональную проекцию плоскости общего положения α(ΔАВС) на плоскости П4, перпендикулярной к плоскости α и к плоскости П1.
(П4 ⊥ ΔABC)

Две плоскости взаимно перпендикулярны, если одна из них содержит прямую перпендикулярную второй плоскости.
П4 ⊥ ΔABC ⇒ (П4 ⊥ h ∧ h ⊂ ΔABC)
П4┴ П1

Пример 6 . Определить истинную величину треугольника АВС
1-й этап. П4 ⊥ ΔАВС
П4 ⊥ П1 ⇒ П4 ⊥ h ⇒ х14 ⊥ h1
2-й этап. П5 II ΔАВС
П5 ⊥ П4 ⇒ х45 ‖ А 4В 4С4

Пример 7. Определить расстояние от точки М до плоскости α(ΔАВС)

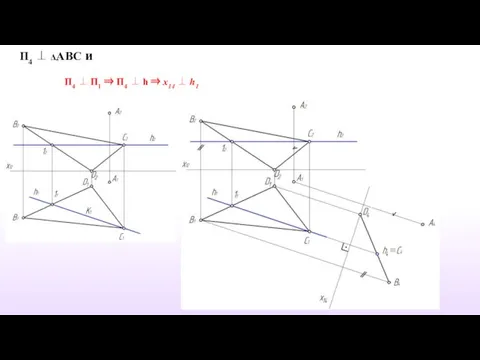
Пример 8. Определить расстояние от точки А до плоскости α(ΔВСD)

П4 ⊥ ΔАВС и
П4 ⊥ П1 ⇒ П4 ⊥ h ⇒ х14 ⊥ h1

Пример9:Определить расстояние от точки А до плоскости α(h∩f)
П4⊥α и П4⊥П1

Пример10.Найти расстояние между скрещивающимися прямыми

Пример11.Найти расстояние между скрещивающимися прямыми
1.П4‖║ l и П4 ⊥П1
x14 ║‖ l1

2.П5 ⊥l и П5 ⊥П4; x45⊥ l4
M5N5⊥m5
M4N4⊥l4

Вращение вокруг горизонтали или фронтали
.
.

Ось вращения i является горизонталью h
радиус вращения точки В- RВ=OB
Σ-плоскость, в которой вращается точка В Σ ┴ h

Определение углов

Угол между пересекающимися прямыми(решено вращением вокруг горизонтали)
1.Строим горизонталь h-ось вращения;2. Строим А1О1┴h1, АО-радиус вращения точки А;3.АО-отрезок общего положения, найдем его натуральную величину. Для этого спроецируем его на П4║АО
4.Повернем точку А в плоскость, перпендикулярную оси
вращения h

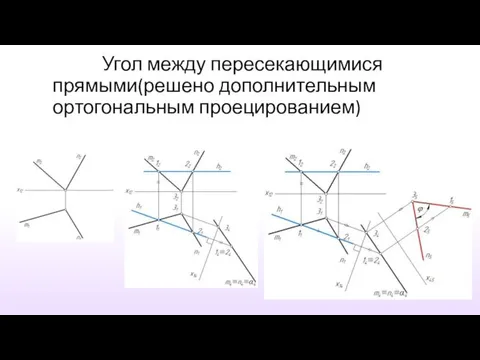
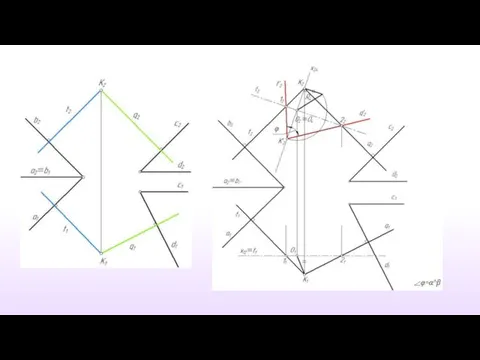
Угол между пересекающимися прямыми(решено дополнительным ортогональным проецированием)

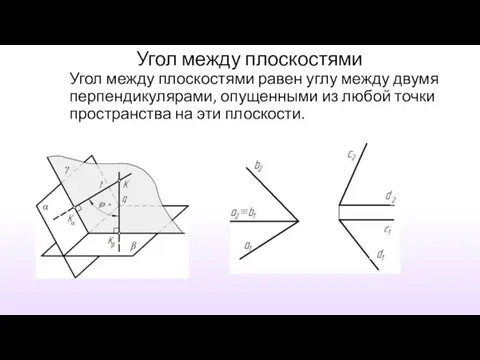
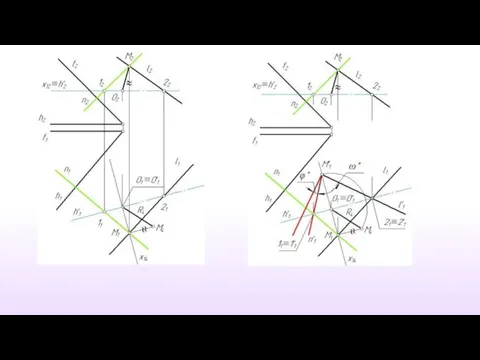
Угол между плоскостями
Угол между плоскостями равен углу между двумя перпендикулярами, опущенными из любой точки пространства на эти плоскости.

Угол между плоскостями(решено дополнительным ортогональным проецированием)

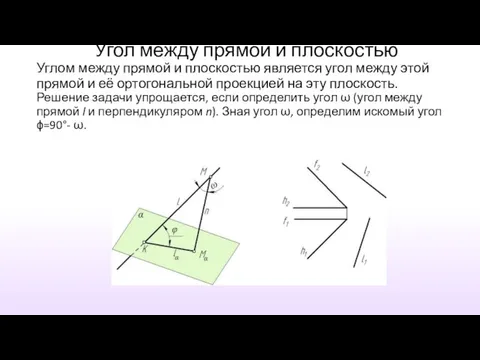
Угол между прямой и плоскостью
Углом между прямой и плоскостью является угол между этой прямой и её ортогональной проекцией на эту плоскость. Решение задачи упрощается, если определить угол ω (угол между прямой l и перпендикуляром n). Зная угол ω, определим искомый угол ϕ=90°- ω.

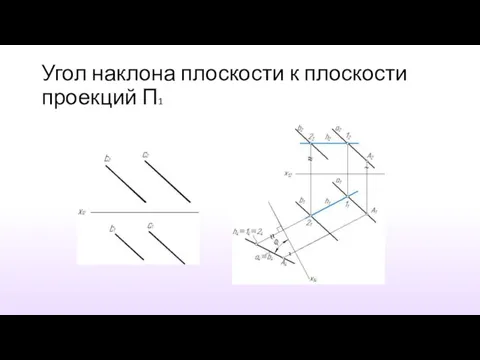
Угол наклона плоскости к плоскости проекций П1

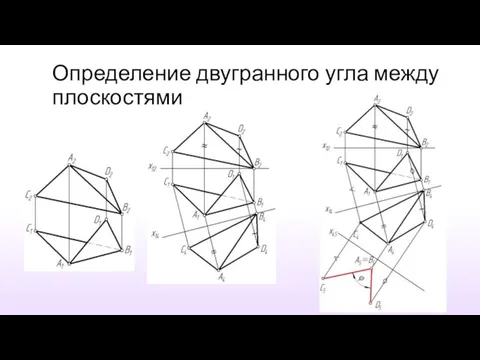
Определение двугранного угла между плоскостями

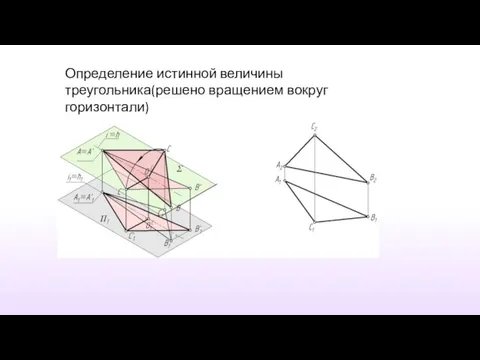
Определение истинной величины треугольника(решено вращением вокруг горизонтали)