Мир наш полон симметрии

Математика владеет не только истиной, но и высшей красотой - красотой
отточенной и строгой, возвышенно чистой и стремящейся к подлинному
совершенству, которое свойственно лишь величайшим образцам искусства.
Бертран Рассел
Математика владеет не только истиной, но и высшей красотой - красотой
отточенной и строгой, возвышенно чистой и стремящейся к подлинному
совершенству, которое свойственно лишь величайшим образцам искусства.
Бертран Рассел

Симметрия …
Мир наш исполнен симметрии. С древнейших времен с ней связаны наши представления о красоте. Наверное, этим объясняется непреходящий интерес человека к правильным многогранникам - удивительным символам симметрии, привлекавшим внимание множества выдающихся мыслителей, от Платона и Евклида до Эйлера и Коши.

Греческая математика, в которой впервые появилась теория многогранников, развивалась под большим влиянием знаменитого мыслителя Платона.
Платон (427–347 до н.э.) – великий древнегреческий философ, основатель Академии и родоначальник традиции платонизма.

Многогранник.
Многогранник - геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, называемыми гранями. Стороны граней называются ребрами многогранника, а концы ребер — вершинами многогранника.

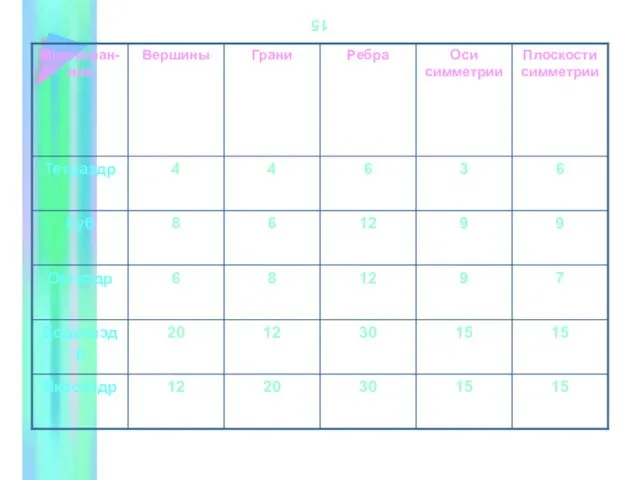
Правильные многогранники.
Существует 5 видов правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.

Евклид вовсе не собирался выпускать систематический учебник геометрии.
Он задался целью написать сочинение о правильных многогранниках, рассчитанное
на начинающих, в силу этого ему пришлось изложить все необходимые сведения.
д'Арси Томпсон
Платоновы тела - трехмерный аналог плоских правильных многоугольников. Однако между двумерным и трехмерным случаями есть важное отличие: существует бесконечно много различных правильных многоугольников, но лишь пять различных правильных многогранников.

Существует семейство тел, родственных платоновым - это полуправильные выпуклые многогранники, или Архимедовы тела. У них все многогранные углы равны, все грани - правильные многоугольники, но нескольких различных типов. Называют 13 или 14 архимедовых тел(число неточное, поскольку псевдоромбокубоктаэдр иногда не причисляют к этому семейству).

Выдающимся вкладом Кеплера в геометрию многогранников является открытие им двух звездных правильных тел. (Всего их четыре; два других нашел французский математик Луи Пуансон в 1809 г.)
Выдающимся вкладом Кеплера в геометрию многогранников является открытие им двух звездных правильных тел. (Всего их четыре; два других нашел французский математик Луи Пуансон в 1809 г.)

Леонард Эйлер (1707-1783)
Теорема Эйлера о соотношении между числом вершин, ребер и граней выпуклого многогранника, доказательство которой Эйлер опубликовал в 1758 г. в «Записках Петербургской академии наук», окончательно навела математический порядок в многообразном мире многогранников.
Вершины + Грани - Рёбра = 2.

15

Кристаллы
Некоторые из правильных и полуправильных тел встречаются в природе в виде кристаллов, другие — в виде вирусов, простейших микроорганизмов.
Кристаллы — тела, имеющие многогранную форму. Вот один из примеров таких тел: кристалл пирита (сернистый колчедан FeS) — природная модель додекаэдра.

Существует гипотеза, по которой ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете. «Лучи» этого кристалла, а точнее его силовое поле, обусловливают икосаэдро-додекаэдрическую структуру Земли, проявляющуюся в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра.
Существует гипотеза, по которой ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете. «Лучи» этого кристалла, а точнее его силовое поле, обусловливают икосаэдро-додекаэдрическую структуру Земли, проявляющуюся в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра.

Многогранники - отнюдь не только объект научных исследований. Их формы - завершенные и причудливые, широко используются в декоративном искусстве.
Надгробный памятник в кафедральном соборе Солсбери
Титульный лист книги Ж. Кузена «Книга о перспективе»