Многогранники

Мир многогранников

Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.
Бертран Рассел

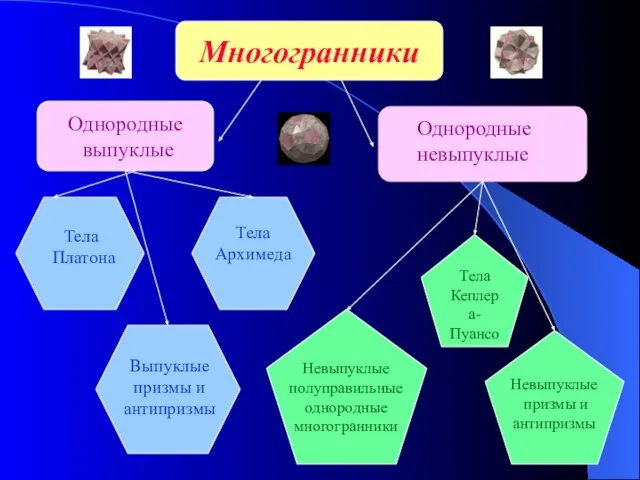
Многогранники
Однородные
выпуклые
Однородные невыпуклые
Тела
Архимеда
Тела
Платона
Выпуклые
призмы и
антипризмы
Тела
Кеплера-
Пуансо
Невыпуклые
полуправильные
однородные
многогранники
Невыпуклые
призмы и
антипризмы

Правильными многогранниками
называют выпуклые многогранники, все грани и все углы которых равны, причем грани - правильные многоугольники.
В каждой вершине правильного многогранника сходится одно и то же число рёбер .
Все двугранные углы при рёбрах и все многогранные углы при вершинах правильного многоугольника равны.
Правильные многогранники - трехмерный аналог плоских правильных многоугольников.

Правильные многогранники
Сколько же их существует?
Рассмотрим развертку вершины многогранника. Каждая вершина может принадлежать трем и более граням.
Сначала рассмотрим случай, когда грани многогранника - равносторонние треугольники. Поскольку внутренний угол равностороннего треугольника равен 60°, три таких угла дадут в развертке 180°. Если теперь склеить развертку в многогранный угол, получится тетраэдр - многогранник, в каждой вершине которого встречаются три правильные треугольные грани. Если добавить к развертке вершины еще один треугольник, в сумме получится 240°. Это развертка вершины октаэдра. Добавление пятого треугольника даст угол 300° - мы получаем развертку вершины икосаэдра. Если же добавить еще один, шестой треугольник, сумма углов станет равной 360° - эта развертка, очевидно, не может соответствовать ни одному выпуклому многограннику.

Теперь перейдем к квадратным граням. Развертка из трех квадратных граней имеет угол 3x90°=270° - получается вершина куба, который также называют гексаэдром. Добавление еще одного квадрата увеличит угол до 360° - этой развертке уже не соответствует никакой выпуклый многогранник.
Три пятиугольные грани дают угол развертки 3*108°=324 - вершина додекаэдра. Если добавить еще один пятиугольник, получим больше 360° - поэтому останавливаемся.
Для шестиугольников уже три грани дают угол развертки 3*120°=360°, поэтому правильного выпуклого многогранника с шестиугольными гранями не существует. Если же грань имеет еще больше углов, то развертка будет иметь еще больший угол. Значит, правильных выпуклых многогранников с гранями, имеющими шесть и более углов, не существует.

Сделаем вывод:
Мы убедились, что существует лишь пять выпуклых правильных многогранников - тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями.
Эти тела еще называют
телами Платона.

огонь
тетраэдр
икосаэдр
октаэдр
гексаэдр
вселенная
додекаэдр
вода
земля
воздух
Начиная с 7 века до нашей эры в Древней Греции создаются философские школы , в которых происходит постепенный переход от практической к философской геометрии. Большое значение в этих школах приобретают рассуждения, с помощью которых удалось получать новые геометрические свойства.
Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора.
Отличительным знаком пифагорейцев была пентаграмма, на языке математики- это правильный невыпуклый или звездчатый пятиугольник.
Пентаграмме присваивалось способность защищать человека от злых духов. Существование только пяти правильных многогранников относили к строению материи и Вселенной. Пифагорейцы, а затем Платон полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды.
Согласно их мнению, атомы основных элементов должны иметь форму различных Платоновых тел.

Число =В-Р+Г называется эйлеровой характеристикой многогранника. Согласно теореме Эйлера, для выпуклого многогранника эта характеристика равна 2. То ,что эйлерова характеристика равна 2 для некоторых знакомых нам многогранников, видно из таблицы.

Теорема Эйлера
В – Р + Г = 2

Тетраэдр
Икосаэдр
Гексаэдр
Додекаэдр
Октаэдр

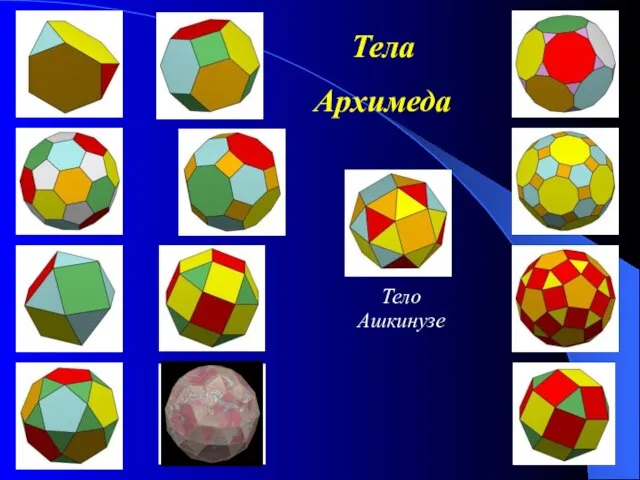
Тела Архимеда
Архимедовыми телами называются полуправильные однородные выпуклые многогранники, то есть выпуклые многогранники, все многогранные углы которых равны, а грани - правильные многоугольники нескольких типов.

Тела
Архимеда
Тело
Ашкинузе

Тела
Кеплера - Пуансо
Среди невыпуклых однородных многогранниковСреди невыпуклых однородных многогранников существуют аналоги платоновых тел - четыре правильных невыпуклых однородных многогранника или тела Кеплера - Пуансо.
Как следует из их названия, тела Кеплера-Пуансо - это невыпуклые однородные многогранники, все грани которых - одинаковые правильные многоугольники, и все многогранные углы которых равны. Грани при этом могут быть как выпуклыми, так и невыпуклыми.

Большой звездчатый
додекаэдр
Большой икосаэдр
Малый звездчатый
додекаэдр

Магнус Веннинджер (1919г.р.)

Многогранники в искусстве
В эпоху Возрождения большой интерес к формам правильных многогранников проявили скульпторы. архитекторы, художники. Леонардо да Винчи (1452 -1519) например, увлекался теорией многогранников и часто изображал их на своих полотнах. Он проиллюстрировал правильными и полуправильными многогранниками книгу Монаха Луки Пачоли ''О божественной пропорции.''
Знаменитый художник, увлекавшийся геометрией Альбрехт Дюрер (1471- 1528) , в известной гравюре ''Меланхолия '‘ на переднем плане изобразил додекаэдр.
художник Эшер

Наука геометрия возникла из практических задач, ее предложения выражают реальные факты и находят многочисленные применения. В конечном счете в основе всей техники так или иначе лежит геометрия, потому что она появляется всюду, где нужна хотя бы малейшая точность в определении формы и размеров. И технику, и инженеру, и квалифицированному рабочему и людям искусства геометрическое воображение необходимо, как геометру или архитектору. Математика, в частности геометрия, представляет собой могущественный инструмент познания природы, создания техники и преобразования мира.
Различные геометрические формы находят свое отражение практически во во всех отраслях знаний: архитектура, искусство.
Многогранники в архитектуре

Великая пирамида была построена как гробница Хуфу, известного грекам как Хеопс. Он был одним из фараонов, или царей древнего Египта, а его гробница была завершена в 2580 году до н.э. Позднее в Гизе было построено еще две пирамиды, для сына и внука Хуфу, а также меньшие по размерам пирамиды для их цариц. Пирамида Хуфу, самая дальняя на рисунке, является самой большой. Пирамида его сына находится в середине и смотрится выше, потому что стоит на более высоком месте.
ЦАРСКАЯ ГРОБНИЦА

ТРИ БАШНИ
Фаросский маяк состоял из трех мраморных башен, стоявших на основании из массивных каменных блоков. Первая башня была прямоугольной, в ней находились комнаты, в которых жили рабочие и солдаты. Над этой башней располагалась меньшая, восьмиугольная башня со спиральным пандусом, ведущим в верхнюю башню.

Александрийский маяк.

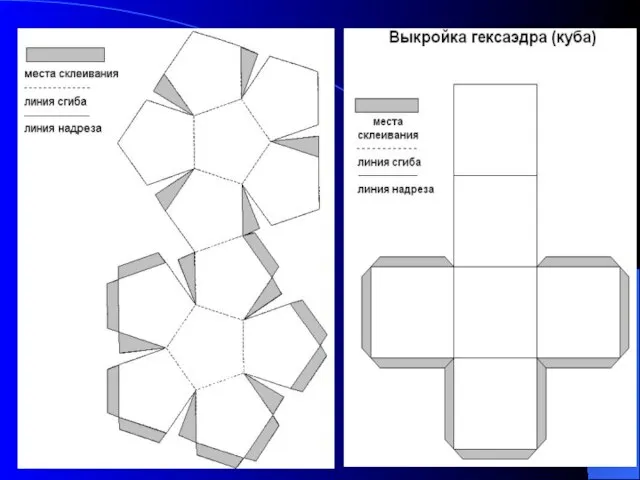
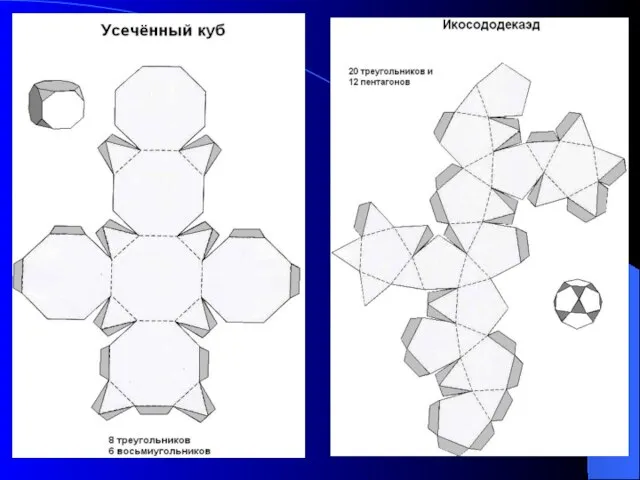
Развёртки
некоторых многогранников
Правильные многогранники (тела Платона)
Тела Архимеда
Тела Кеплера-Пуансо
Невыпуклые полуправильные многогранники

Выкройка додекаэдра