Нечеткая логика

Неклассические логики
Нечеткая логика
Временная логика
Алгоритмическая логика
Модальная логика

Нечёткая логика

Предпосылки
Возникла необходимость в аппарате, способном моделировать рассуждения на основе сложных причинно-следственных связей.
«Почти всегда можно сделать такой же самый продукт без нечеткой логики, но с нечеткой будет быстрее и дешевле»
Лотфи Заде
«Бинарная логика – не более чем роковая ошибка античной цивилизации»
Барт Коско

Нечеткие множества
Лотфи Заде (Lotfi Zadeh)
Характеристикой нечеткого множества выступает функция принадлежности.
ности к нечеткому множеству F, представляющая собой обобщение понятия характеристической функции обычного множества.
– степень принадлеж-
Zadeh L.A. Fuzzy Sets // Information and control. – 1965. Vol.8. – P.338-353.
В классической теории множеств принадлежность объекта x множеству С определяется характеристической функцией вида:

Нечеткое множество – это подмножество А некоторого четкого множества-носителя, каждому элементу которого сопоставлена степень его принадлежности множеству A.
Нечеткое множество полностью определяется заданием функции принадлежности μА(x), μА(x) ∈ [0,1].

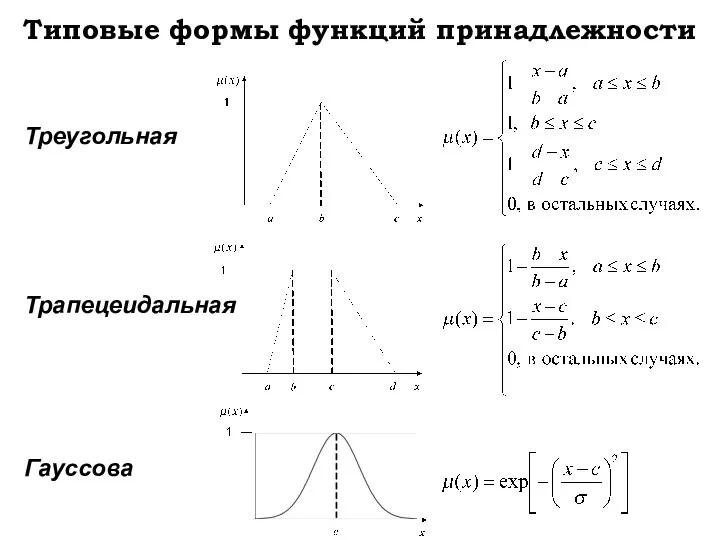
Типовые формы функций принадлежности
Треугольная
Трапецеидальная
Гауссова

Операции над нечеткими множествами
Объединением нечетких множеств A и B называется нечеткое множество A∪B с функцией принадлежности:
Пересечением нечетких множеств A и B в X называется нечеткое множество A∩B с функцией принадлежности:
Дополнением нечеткого множества A называется нечеткое множество
с функцией принадлежности:

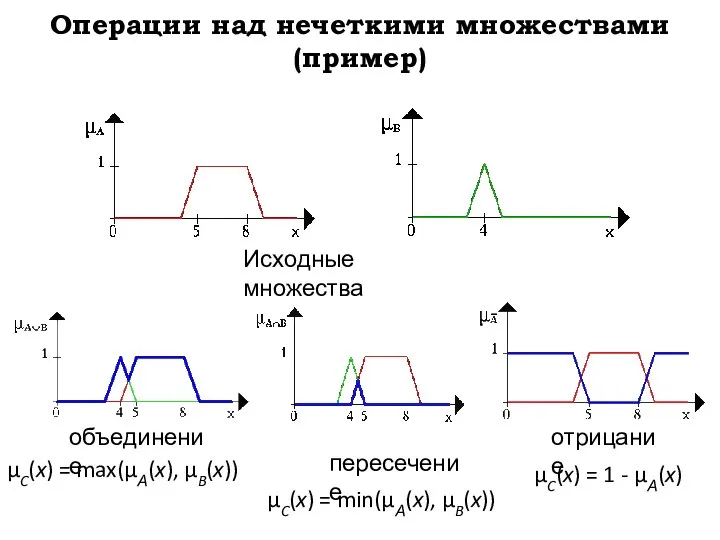
Операции над нечеткими множествами
(пример)
Исходные множества
объединение
пересечение
отрицание
μC(x) = min(μА(x), μB(x))
μC(x) = max(μА(x), μB(x))
μC(x) = 1 - μА(x)

Алгебраические операции
На основе операции алгебраического произведения определяется операция возведения в степень a нечёткого множества А, где a – положительное число
Частные случаи

Нечеткая переменная описывается набором (N, X, F) , где
N – это название переменной,
X – универсальное множество,
F – нечеткое множество на X, представляющее собой нечеткое ограничение на значения x нечеткой переменной N.
Нечёткая переменная = наименование переменной + область определения A + функция принадлежности μА.
Нечёткая переменная – именованное нечеткое множество: например, нечеткая переменная «высокий рост».
Нечёткая переменная

Лингвистическая переменная
N – название переменной;
T – множество значений (базовое терм-множество), его элементы представляют собой названия нечетких переменных;
X – универсальное множество;
G – синтаксическое правило, по которому генерируются новые термы с применением слов естественного или формального языка;
P – семантическое правило каждому значению лингвистической переменной ставит в соответствие нечеткое подмножество множества X.
Лингвистическая переменная (N, Т, X , G, P) состоит из:

Примеры лингвистических переменных
Бизнес = {«малый», «средний»}
Температура в комнате = {«холодно», «комфортно», «жарко»}
Процентная ставка = {«высокая», «низкая»}
Термы –
наименования
нечетких переменных
Лингвистическая
переменная

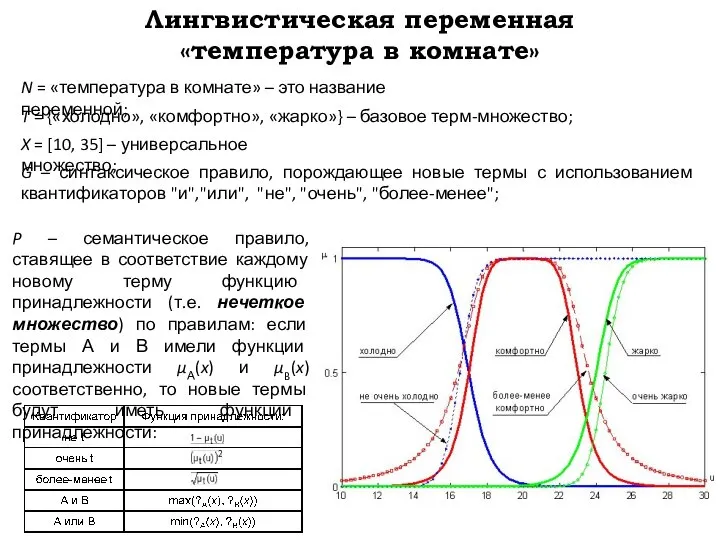
Лингвистическая переменная
«температура в комнате»
N = «температура в комнате» – это название переменной;
X = [10, 35] – универсальное множество;
T = {«холодно», «комфортно», «жарко»} – базовое терм-множество;
G – синтаксическое правило, порождающее новые термы с использованием квантификаторов "и","или", "не", "очень", "более-менее";
P – семантическое правило, ставящее в соответствие каждому новому терму функцию принадлежности (т.е. нечеткое множество) по правилам: если термы А и В имели функции принадлежности μА(x) и μB(x) соответственно, то новые термы будут иметь функции принадлежности:

Нечёткие отношения

Нечеткие правила
Нечеткие знания формулируются в виде нечетких продукционных правил вывода в форме «если-то» (if-then rule):
ЕСЛИ x это A, ТО y это B
где A и B – это лингвистические переменные и соответствующие им функции принадлежности
Левая часть правила называется условием, или предпосылкой, правая часть – следствием, или заключением.
Для n переменных правило Ri примет вид нечеткого рассуждения:
Ri: ЕСЛИ (x1 это Ai1) … И … (xn это Ain), ТО (y это Bi).
Уровни представления нечетких правил:
уровень поверхностной структуры – правила сформулированы только в лингвистической форме;
уровень глубинной структуры – поверхностная структура правила вместе со значениями функций принадлежности для каждого терма лингвистической переменной.

Модели нечеткого вывода
Пусть в базе правил системы нечеткого вывода, имеется m правил вида:
R1: ЕСЛИ (x1 это A11) … И … (xn это A1n), ТО (y это B1)
Ri: ЕСЛИ (x1 это Ai1) … И … (xn это Ain), ТО (y это Bi)
Rm: ЕСЛИ (x1 это Am1) … И … (xn это Amn), ТО (y это Bm)
… … …
… … …
где
– имена входных переменных;
– имя выходной переменной;
– определенные функции принадлежности.
y
Результатом нечеткого вывода является четкое значение переменной
на основе заданных четких значений
.

Этапы нечёткого логического вывода
Формирование базы правил
2. Фаззификация входных параметров – введение нечеткости – процесс нахождения функции принадлежности нечетких множеств. Устанавливается соответствие между численным значением входной переменной системы нечеткого вывода и значением функции принадлежности соответствующей ей лингвистической переменной.
3. Агрегирование – определение степени истинности каждого из подзаключений по каждому из правил
4. Активизация подусловий в нечетких правилах – нечеткие подмножества, назначенные для каждой выходной переменной, объединяются вместе
5. Дефаззификация – определение четких значений выходных переменных

Правило Мамдани (Mamdani)
Импликации
соответствует нечёткое отношение c функцией
принадлежности:

Нечеткий вывод по способу Мамдани (Mamdani)
Определяются степени истинности, т.е. значения функций принадлежности для левых частей каждого правила (предпосылок):
Определяются уровни «отсечения» для левой части каждого из правил:
Находятся «усеченные» функции принадлежности
Композиция полученных усеченных функций
Приведение к четкости, центроидный метод:
Первый нечеткий контроллер для управления паровым двигателем
E.H. Mamdani, S. Assilian. An experiment in linguistic synthesis with a fuzzy logic controller. 1975.

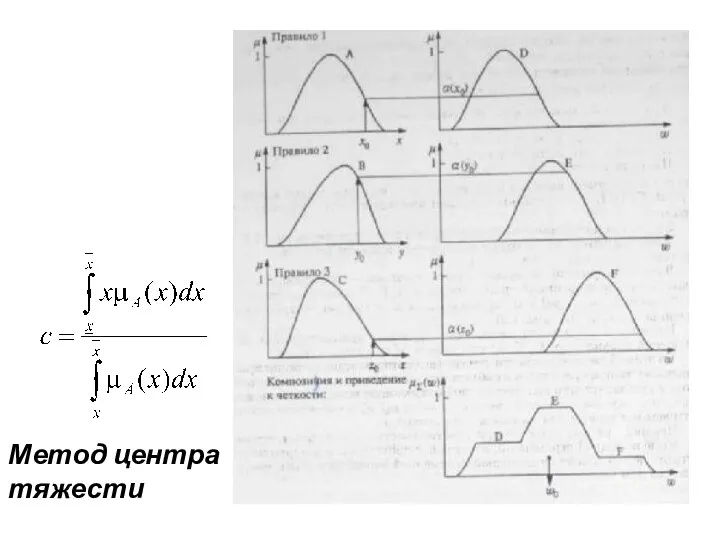
Метод центра тяжести

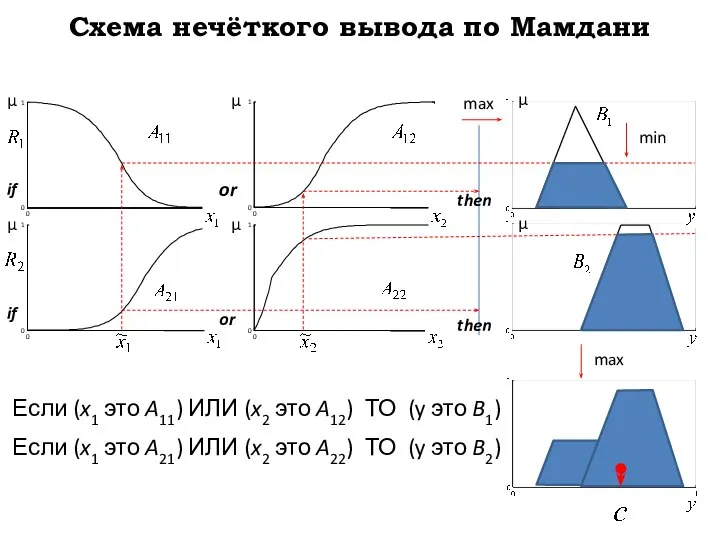
Схема нечёткого вывода по Мамдани
max
µ
µ
µ
µ
µ
µ
or
or
then
if
if
then
min
max
Если (x1 это A11) ИЛИ (x2 это A12) ТО (y это B1)
Если (x1 это A21) ИЛИ (x2 это A22) ТО (y это B2)

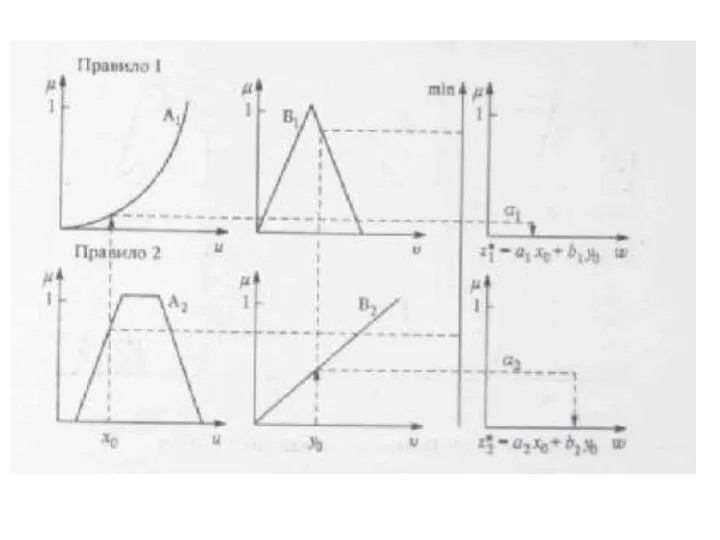
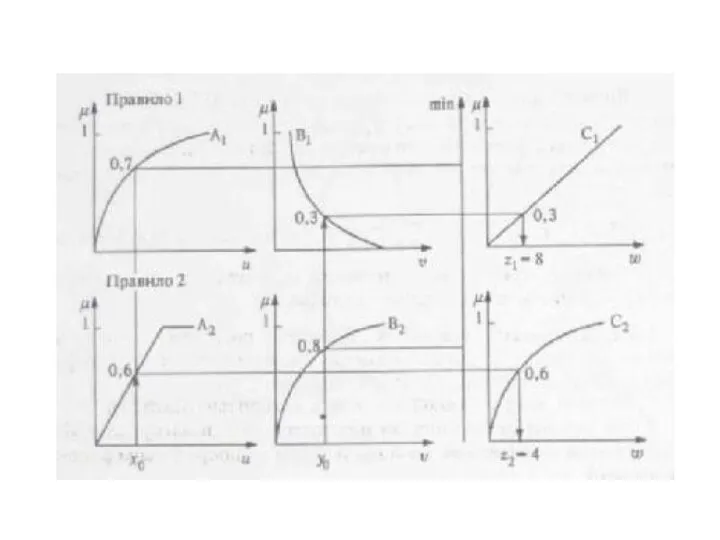
Нечеткий вывод по Сугено (Sugeno)
Определяются степени истинности.
Определяются уровни «отсечения» предпосылок правил αi и рассчитываются индивидуальные выходы правил
Итоговая четкая величина вычисляется как средневзвешенное:
где pi0, [pij] – коэффициенты полинома или цифровые веса. В адаптивных системах подбираются в процессе обучения.
Набор правил следующего вида:
Ri: ЕСЛИ (x1 это Ai1) … И … (xn это Ain), ТО y = f (X),
f (X) – некоторая четкая функция, полином первого порядка:
Первый нечеткий контроллер в Японии для очистки воды
M.Sugeno and T. Takagi . A new approach to design of fuzzy controller. 1983.

Нечеткий вывод по способу Tsukamoto
Определяются степени истинности, т.е. значения функций принадлежности для левых частей каждого правила (предпосылок):
Определяются уровни «отсечения» для левой части каждого из правил:
Находятся чёткие значения для каждого из исходных правил
Определяется чёткое значение переменной вывода

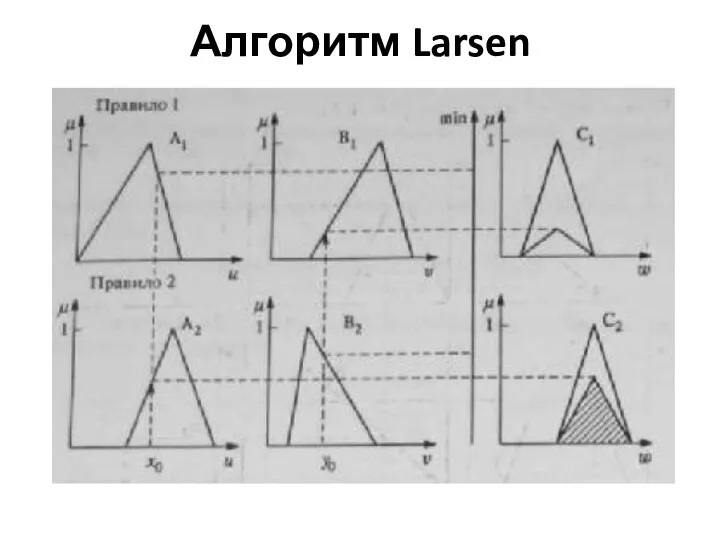
Алгоритм Larsen

Fuzzy Approximation Theorem
Бартоломей Коско
(Bart Kosko)
FAT- Теорема:
Любая математическая система может быть с необходимой точностью аппроксимирована системой на нечеткой логике.
Kosko B. Fuzzy systems as universal approximators
// IEEE Transactions on Computers, vol. 43, No. 11,
November 1994. – P. 1329-1333.

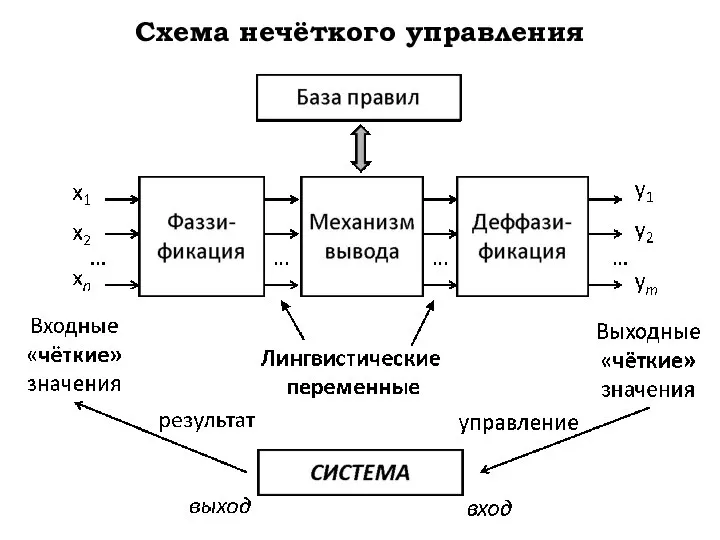
Схема нечёткого управления

Практическое применение
1970-е – Мамдани и Ассилиан построили первый нечеткий контроллер для лабораторной модели парового двигателя
1982 – в Дании Холмблад и Остергард внедрили нечеткую логику в управление процессом обжига цемента
1987 – фирма Hitachi разработала нечеткую систему управления движением электропоезда в метро города Сендай
1990 – в Японии зарегистрировано около 30 патентов. Серийное производство бытовых приборов с нечетким управлением:
камеры с автоматической фокусировкой (Canon)
кондиционеры воздуха (Mitsubishi)
стиральные машины (Panasonic и Matshushita)
автоматическая трансмиссия (Honda и Nissan)
нечеткий контроллер лифта (Toshiba )

Практическое применение (продолжение)
1993 – Барт Коско доказал теорему о нечеткой аппроксимации (Fuzzy Approximation Theorem)
1997 – язык нечеткого управления Fuzzy Control Language внесен в Международный стандарт программируемых контроллеров IEC 1131-7
Наши дни – Области применения: медицинская диагностика, техническая диагностика, финансовый менеджмент, управление персоналом, биржевое прогнозирование, распознавание образов, разведка ископаемых, выявление мошенничества, управление компьютерными сетями, управление технологическими процессами, управление транспортом, поиск информации в Интернете, радиосвязь и телевидение. Спектр приложений от бытовых видеокамер, пылесосов и стиральных машин до средств наведения ракет ПВО и управления боевыми вертолетами.

Пример
После рабочего дня Вы проголодались и решили зайти поужинать в незнакомое кафе. Предположим, что степень своей удовлетворенности от кафе Вы будете выражать в размере чаевых, которые колеблются в интервале от 0 до 25% от счета заказа. Щедрость чаевых будет зависеть от двух факторов:
качество еды, которое будет оцениваться, как:
вкусно
невкусно
качество обслуживания, оцениваемое по шкале:
отличное
среднее
плохое
Еда была достаточно хорошей, а вот сервис был на низком уровне

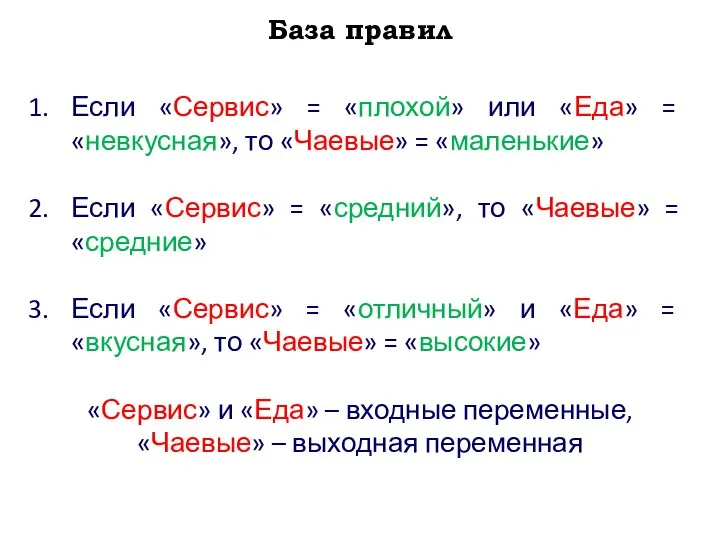
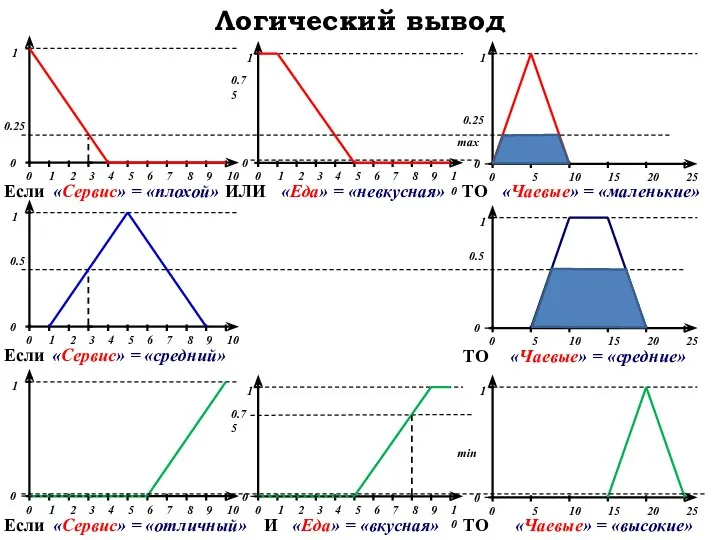
База правил
Если «Сервис» = «плохой» или «Еда» = «невкусная», то «Чаевые» = «маленькие»
Если «Сервис» = «средний», то «Чаевые» = «средние»
Если «Сервис» = «отличный» и «Еда» = «вкусная», то «Чаевые» = «высокие»
«Сервис» и «Еда» – входные переменные,
«Чаевые» – выходная переменная

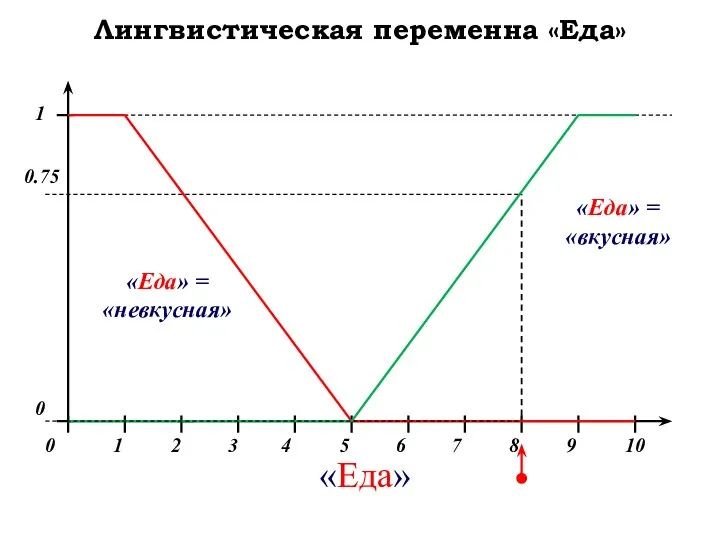
Лингвистическая переменна «Еда»

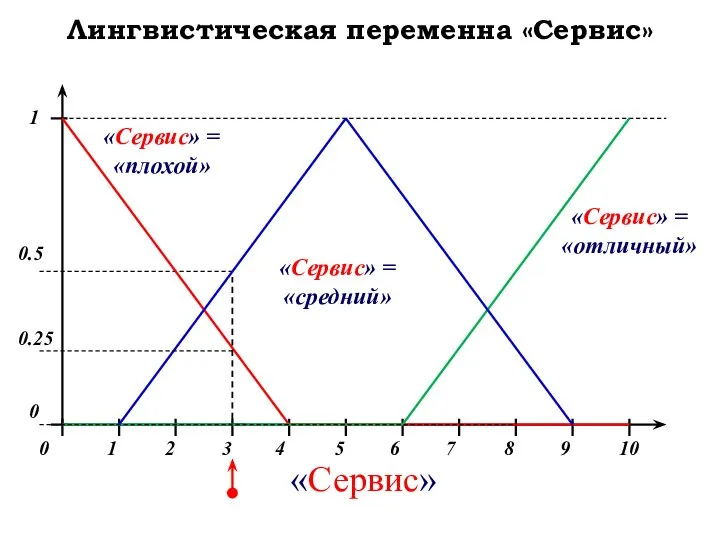
Лингвистическая переменна «Сервис»

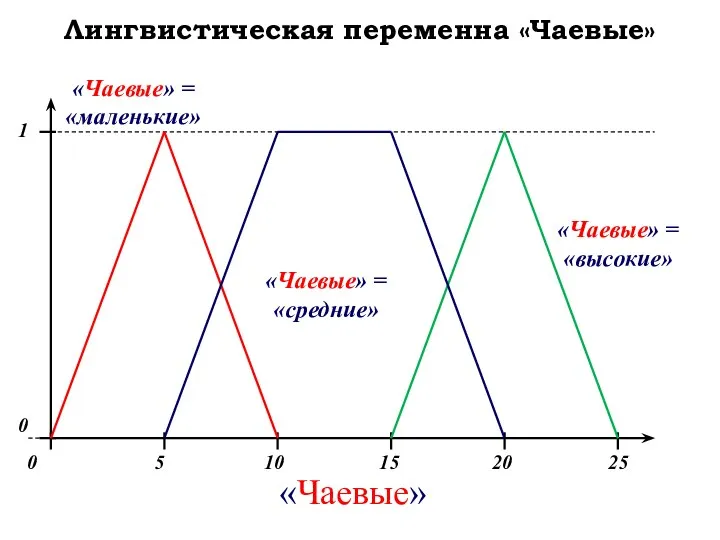
Лингвистическая переменна «Чаевые»

Логический вывод
«Чаевые» = «средние»

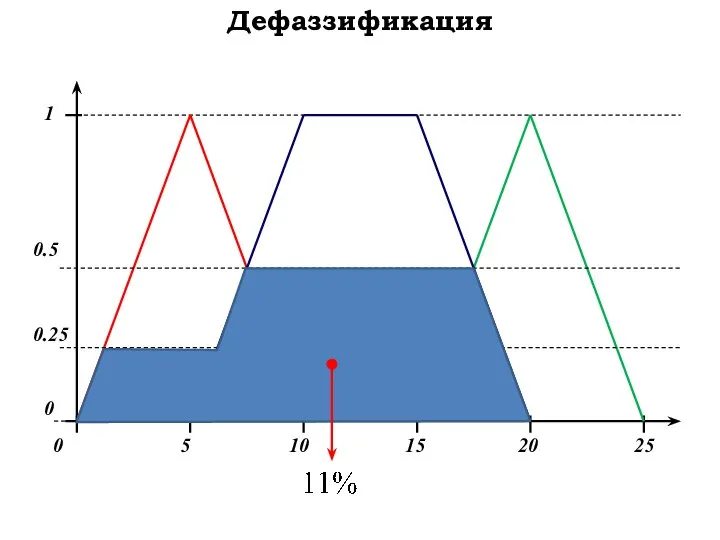
Дефаззификация