Слайд 2Нормирование
Суть: перейти от рассмотрения величин, имеющих интервал значений [x min, x max]

к рассмотрению нормированного интервала [-1, 1] или [0, 1].
Слайд 3Зачем нормировать?
Сходные модели для качественно подобных систем.
Как следствие, упрощение жизни разработчиков.

Слайд 4Как нормировать? (1)
+: Используется весь интервал [-1, 1].
-: Нули исходной и нормированной величины не
![Как нормировать? (1) +: Используется весь интервал [-1, 1]. -: Нули исходной](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/464447/slide-3.jpg)
совпадают.
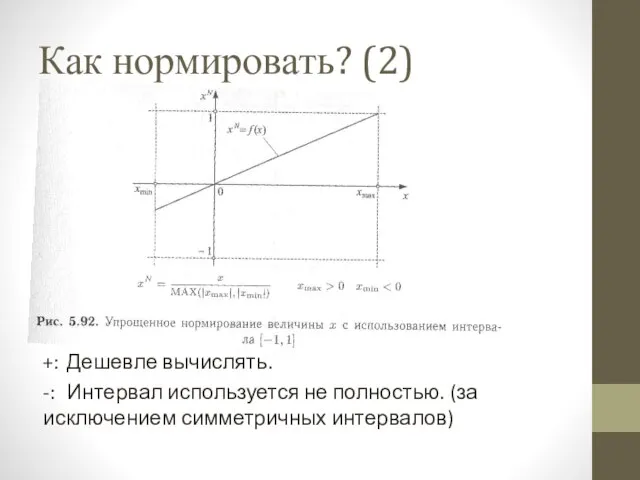
Слайд 5Как нормировать? (2)
+: Дешевле вычислять.
-: Интервал используется не полностью. (за исключением симметричных интервалов)
Слайд 6Денормирование
На выходе нормированной нечёткой модели получаем выходное значение с симметричным интервалом [-1,

1].
Денормированное выходное значение может иметь асимметричный интервал изменения.
[-1, 1] -> [y min, y max]
Слайд 7Как денормировать? (1)
+: Используется весь интервал [y min, y max].
-: Нули исходной и нормированной
![Как денормировать? (1) +: Используется весь интервал [y min, y max]. -:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/464447/slide-6.jpg)
величины не совпадают.
Слайд 8Как денормировать? (2)
Можно получить значение меньше y min!

Слайд 9Как денормировать? (3)
Y max недостижим!

Слайд 10Нормирование: итого
Нормирование и денормирование – линейные преобразования:
Нормированная нечёткая модель:

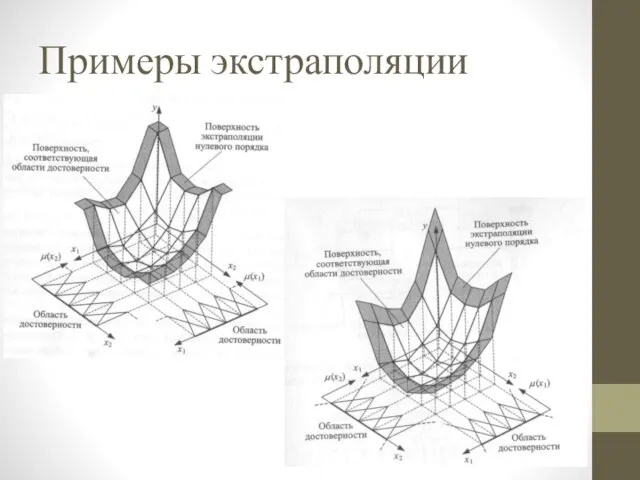
Слайд 11Экстраполяция
Экстраполяция – расширение поверхности модели на внешние области, для которых отсутствуют результаты
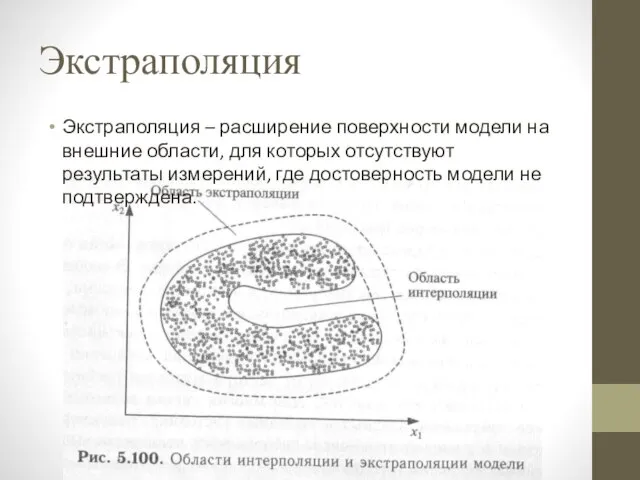
измерений, где достоверность модели не подтверждена.
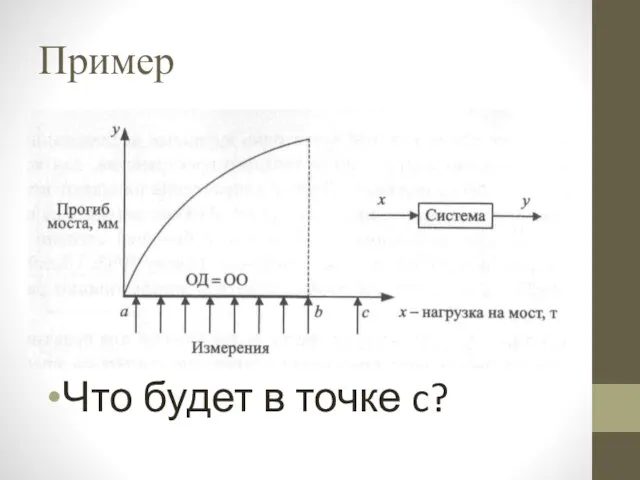
Слайд 13Угадаем?
Экстраполяция модели носит характер предположения!

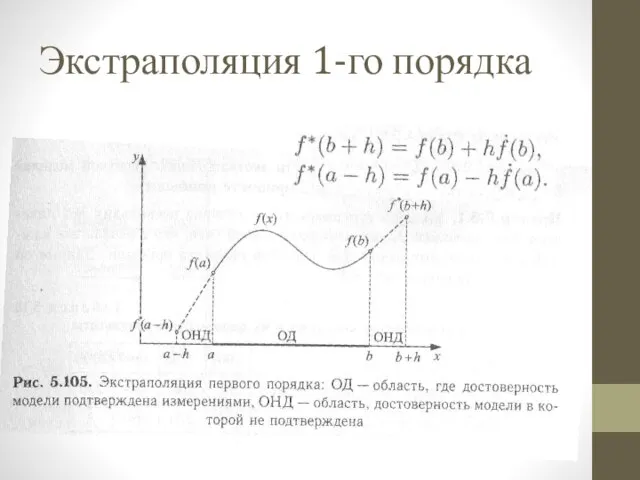
Слайд 16Экстраполяция n-го порядка
Можно использовать экстраполяции более высоких порядков, однако полученные значения останутся

лишь необоснованными предположениями.
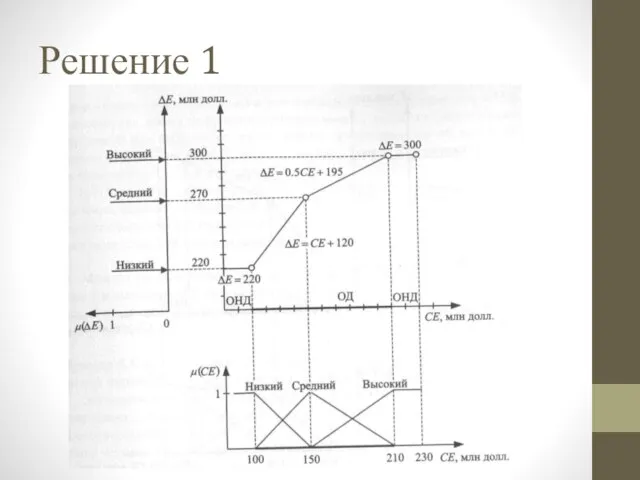
Слайд 20Что значит μ(CE) > 1?
Значения в интервале [1, ∞) – степень сходства

с типовым элементом нечёткого множества.
Значения в интервале (-∞, 0] – степень несходства или различия с типовым элементом нечёткого множества.
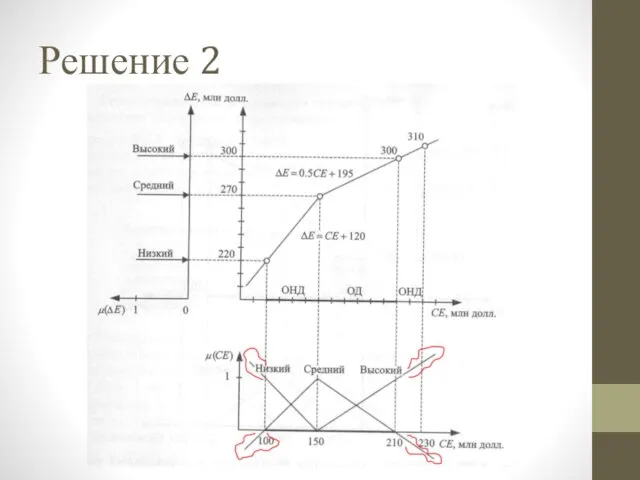
Слайд 22Замечания
Расширение нечёткой модели не обязательно должно быть линейным.
Расширение области определения не должно

быть большим – чем меньше, тем лучше.


![Как нормировать? (1) +: Используется весь интервал [-1, 1]. -: Нули исходной](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/464447/slide-3.jpg)


![Как денормировать? (1) +: Используется весь интервал [y min, y max]. -:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/464447/slide-6.jpg)










 Общественно-активная школа: эффективность и качество.
Общественно-активная школа: эффективность и качество. 197368
197368 С какво свързваш древногръцкото облекло?
С какво свързваш древногръцкото облекло? Презентация на тему Экономика и ее роль в обществе
Презентация на тему Экономика и ее роль в обществе Фотоальбом. Велосипеди
Фотоальбом. Велосипеди Узорочья Севера
Узорочья Севера Цветы для моей семьи
Цветы для моей семьи Открытые горные работы, их элементы и терминология
Открытые горные работы, их элементы и терминология Бизнес инсайт. Продуктивность как система
Бизнес инсайт. Продуктивность как система Где летит птица?
Где летит птица? Итоги 1 полугодия 2010-2011 уч.года
Итоги 1 полугодия 2010-2011 уч.года Творческий проект Кукла своими руками
Творческий проект Кукла своими руками Буквы О-Ё после шипящих и Ц
Буквы О-Ё после шипящих и Ц Формы взаимодействия с семьей (из опыта работы)
Формы взаимодействия с семьей (из опыта работы) КОММУНИКАТИВНАЯ ПОЛИТИКА ХОЛДИНГОВ
КОММУНИКАТИВНАЯ ПОЛИТИКА ХОЛДИНГОВ Государственное регулирование цен на лекарственные средства на региональном уровне и проблемы, возникающие в рамках действующег
Государственное регулирование цен на лекарственные средства на региональном уровне и проблемы, возникающие в рамках действующег Презентация прочитанной книги
Презентация прочитанной книги Филиал ООО компания Тензор. Сфера торгов
Филиал ООО компания Тензор. Сфера торгов Рекуперативный воздухонагреватель, с использованием жидких горючих отходов.
Рекуперативный воздухонагреватель, с использованием жидких горючих отходов. Интерактивно-аналитический онлайн-сервиса Калькулятор процедур
Интерактивно-аналитический онлайн-сервиса Калькулятор процедур Элла Фицджеральд - выдающаяся джазовая певица, актриса 1917-1996
Элла Фицджеральд - выдающаяся джазовая певица, актриса 1917-1996 Места на направление Товароведение
Места на направление Товароведение Праця неповнолітніх
Праця неповнолітніх Прямолинейное распространение света
Прямолинейное распространение света Документовед он-лайн сервис оформления документов Документы для регистрации общества с ограниченной ответственностью за 15 минут.
Документовед он-лайн сервис оформления документов Документы для регистрации общества с ограниченной ответственностью за 15 минут. Как правильно оформить презентацию и web-сайт?
Как правильно оформить презентацию и web-сайт? Капитализм XVIII века. Промышленный переворот в Англии
Капитализм XVIII века. Промышленный переворот в Англии Работать с молодёжью: как?
Работать с молодёжью: как?