Слайд 2Цели урока:
Закрепить:
знание формул квадратного уравнения;
2)формулы сокращенного умножения;
3)построение точки по её координатам

и нахождение координаты точек.
Развивать культуру математической речи, уметь выступать перед аудиторией подготовленным сообщением.
Приучать работе со справочной, дополнительной литературой.
Слайд 3Круг
часть плоскости, ограниченная окружностью (содержащая ее центр). Площадь круга S =∏ R2,

где R — радиус окружности, а
∏ = 3,141592654 — отношение длины окружности к диаметру
Слайд 4квадрат
(от лат. quadratus — четырехугольный),
1) прямоугольник с равными сторонами.
2) Вторая степень числа
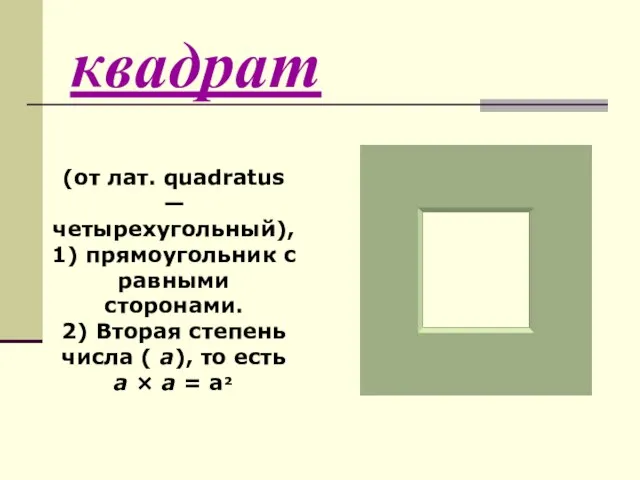
( а), то есть
а × а = а²
Слайд 5Треугольник
ТРЕУГОЛЬНИК, часть плоскости, ограниченная тремя отрезками прямых (сторонами треугольника), имеющими попарно по

одному общему концу (вершины треугольника). Сумма всех углов треугольника равна (180°).
Слайд 6Команда «Треугольники»
Решите квадратные уравнения и угадайте фамилию одного известного французского математика.
И х2

– 3х – 4 =0
Т х2 + 4х +3 =0
В х2 -2х =0
Е х2 – 4 =0
Слайд 7Команда”Квадрат”
Найдя букву ,которая соответствует каждой координате, вы узнаете фамилию французского математика и

философа.
О
х
у
1
2
3
4
1
2
3
4
5
Б
О
Л
Ы
Ц
Ш
Г
М
И
Т
П
Н
Р
Я
Х
К
З
Ж
Е
У
Ю
Д
А
В
Щ
Слайд 8Команда” Круг”
Упростив выражения и расставив их по местам в таблице вы узнаете

имя древнегреческого ученого (III в).
А (а -9)2 – (81 + а2)
Д (с +b)(c - b) – (5c2 –b2)
И (х +3)2 – 6х – 9
Н (р - 3)(р + 3) – р2
О 6ab +(7 – 6ab)
T (10dc - 3) -10dc
Ф 272 -262
Слайд 9Решение.
(команда«Треугольников»)
Франсуа Виет
(1540- 1603)

Слайд 10Решение.(команда «Квадрат»)
Рене Декарт
(1596 -1650)

Слайд 12История квадратного уравнения.
Квадратные уравнения в Индии.
Задачи на квадратное уравнение встречаются в

астрономическом трактате» Ариабхаттиам»составленном в 499г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый – Брахмагупта (VIIв) изложил общее правило решения квадратных уравнений. Его правило по существу совпадает с современным.
Квадратные уравнения в Древнем Вавилоне.
Квадратные уравнения умели решать вавилоняне около 2000лет до н.э. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
Квадратные уравнения в Европе(ХIII―ХVIIвв.)
Формы решения квадратных уравнений по образцу ал-Хорезми в Европе были впервые изложены в «Книге абаха», написанной в 1202г. Итальянским математиком Леонардо Фибоначчи. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду х²+ bx= c было сформировано в Европе в 1544г.М.Штифелем.Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские ученые Тарталья, Кардано, Бомбелли среди первых в ХVIв. Учитывают,помимо положительных, и отрицательные корни. Лишь в ХVIIв. Благодаря трудам Жиррара, Декарта, Ньютона и других ученых, способ решения квадратных уравнений принимает современный вид.
Слайд 13Урок – соревнование.
«Математика 6 класс.»
Ванцян А.Г.
«Предмет „математика” настолько серьезен, что полезно

не упускать случая делать его немного занимательным» -
писал выдающийся французский ученый ХVII века Блез Паскаль.
Слайд 14Все действия с десятичными дробями.
Цель:
Повторить, обобщить и систематизировать знания , умения

и навыки по теме.
Способствовать развитию творческой деятельности учащихся, потребности к самообразованию.
Воспитывать культуру общения.
Слайд 15Разминка.
1.Какое слово употребляется и в математике, и на охоте?
(дробь)
2. Какое слово пропущено?
Обыкновенная

дробь – дробная черта; десятичная дробь - ……
(запятая).
3. Найдите закономерность и вместо»?»поставьте число.
а) 7,1 2,5 1,5 3,2 б) 10,8 2,6 5,3 1,2
9,6 ? 8,2 ?
Решение: 4,7; 4,1.
Слайд 16Догадайтесь.
3/6; 5/4; 15/25; 4/10; 10/7; 7/9; 24/8.
Решение:
1) 3/6,15/25, 4/10 ,7/9.
2 )

5/4,10/7,24/8.
3) 5/4, 15/25, 4/10.
14,8 ; 3,21 ; 9,003; 71,083
Решение: десятых, целых, тысячных, сотых.
Слайд 17Лесенка
5,3+3
18,7 - *
* ·10
25% от *
6,2 - 3
196,8 + *
* :10
75% от
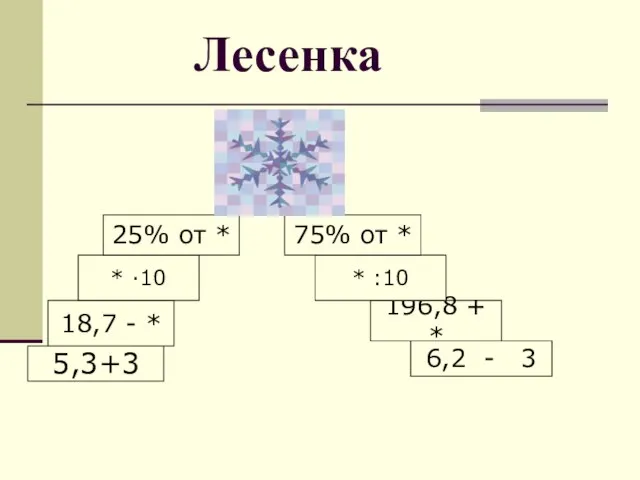
*
Слайд 20Экология.
Над заводом – 0,86%
Над городом - 0,129%
Над селом – 1/100%
Над водой –

1/1000%
Над лесом – 0,0003%
Ответ: 0,0003%,0,001%,0,01%,0,129%0,86%
Слайд 21Конкурс реставраторов.
2,0…< 2,02;
0,368 < 0,3..8
6,413> 6,4…8
1,892 < 1,89...

Слайд 22Найдите лишнее.
7,1; 1/6; 0,5; 3,4.
Решение: 1/6 т.к.обыкновенная дробь , а остальные десятичные
5,8;

3,6; 0,34; 6,7.
Варианты ответа: 1)0,34 –меньше
единицы, а остальные дроби больше единицы;
2) 6,7 – т.к. оканчивается нечетной цифрой;
3) 0,34 – т.к. у неё два десятичных знака ,а у остальных один.
Слайд 23Помогите сказочным героям.
Округлите дробь:
10,7628 до десятых, сотых, тысячных.
Решение: 10,7628 ≈ 10,8; 10,7628

≈ 10,76;
10,7628 ≈ 10,763.
Найдите 35% от 60
Решение: 60 · 0,35 =21
Найдите число а если известно, что 15% от а составляет 90
Решение: 90: 0,15=600
Сравни дроби: 0,7 и 0,75
Решение: 0,7 < 0,75
Слайд 25Удачи.
1. 3,7+8,2 8. 0,25-у=0,01
2. 14,27-3,25 9. 0,725·10
3. 4+3,25 10. а+12,7=15,8
4. 15-3,1

11. 18,4:10
5. 12+0,56 12. 41:10
6. 5,6-3,54 13. 0,025 ·100
7. 23,5-19,4























 DREAM LAND
DREAM LAND Особенности использования TimesTen In-Memory Database в высоконагруженной среде
Особенности использования TimesTen In-Memory Database в высоконагруженной среде Игра в черное и белое
Игра в черное и белое Вычитание и сказка "Царевна-лягушка" 2 класс
Вычитание и сказка "Царевна-лягушка" 2 класс Органическая химия
Органическая химия Вербальные средства и процесс слушания в деловой коммуникации
Вербальные средства и процесс слушания в деловой коммуникации Літературна_та_загальнонародна_національна_мова
Літературна_та_загальнонародна_національна_мова Лев Толстой и Ясная Поляна
Лев Толстой и Ясная Поляна Центр психологической помощи
Центр психологической помощи БЕЗОПАСНОСТИ ДОРОЖНОГО ДВИЖЕНИЯ – ОСОБОЕ ВНИМАНИЕ
БЕЗОПАСНОСТИ ДОРОЖНОГО ДВИЖЕНИЯ – ОСОБОЕ ВНИМАНИЕ Выход из плоскости в пространство. Способы макетирования из одного листа бумаги
Выход из плоскости в пространство. Способы макетирования из одного листа бумаги На заре человечества
На заре человечества Скульптуры разных эпох и стилей
Скульптуры разных эпох и стилей Закаляйся - если хочешь быть здоров!
Закаляйся - если хочешь быть здоров! Конкурс на «Лучшую процедурную медсестру»
Конкурс на «Лучшую процедурную медсестру» Творчество Александра Блока на примере цикла стихов «Стихи о Прекрасной Даме»
Творчество Александра Блока на примере цикла стихов «Стихи о Прекрасной Даме» Наличные и электронные деньги
Наличные и электронные деньги УЗЧ-
УЗЧ- реализация программы нравственного воспитания
реализация программы нравственного воспитания Британия, Британия, туманная страна…
Британия, Британия, туманная страна… Английские слова
Английские слова Земля хороша собой… (пишем этюды, или зарисовки с натуры)
Земля хороша собой… (пишем этюды, или зарисовки с натуры) Основы работы в ВикиВики (практика) Нацкевич Юлия Попова Светлана Дерябин Александр
Основы работы в ВикиВики (практика) Нацкевич Юлия Попова Светлана Дерябин Александр Презентация на тему Речевая разминка на уроках чтения
Презентация на тему Речевая разминка на уроках чтения Функции науки об управлении персоналом
Функции науки об управлении персоналом Средняя общеобразовательная школа № 17 с углубленным изучением отдельных предметов
Средняя общеобразовательная школа № 17 с углубленным изучением отдельных предметов Lection 14 tanini skzbnaxbjurner
Lection 14 tanini skzbnaxbjurner Атомные аварии
Атомные аварии