О природе космологических сил отталкивания

. Исходные уравнения

. Λ-член

. Космологические уравнения А.А.Фридмана с Λ-членом

. Эйнштейновские силы отталкивания

. Обобщенные уравнения Эйнштейна

. Обобщенные уравнения А.А.Фридмана

. Обобщенные уравнения А.А.Фридмана, «Δ-энергия»

. Случай эйнштейновских сил

. ΛCDM-модель

. С-модель (C-centrifugal)

. С-модель (продолжение)

. S-модель (S-simple)

. Нерелятивистская Вселенная (идеализация)

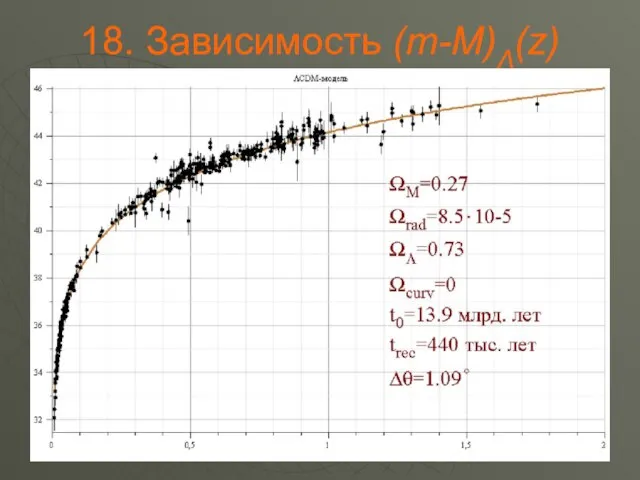
. Зависимость (m-M)(z) для сверхновых типа Ia

. Зависимость r(z)

. Анизотропия реликтового излучения

. Зависимость (m-M)Λ(z)

. Зависимость (m-M)C(z)
2
2
1

. S-модель

. Результаты
Показано, что в уравнениях ОТО, кроме эйнштейновских сил отталкивания, описываемых Λ-членом, теоретически допустимы и другие космологические силы отталкивания.
Доказана возможность и целесообразность модификации уравнений Эйнштейна. Она связана с введением в уравнения Эйнштейна дополнительных слагаемых, учитывающих влияние некоторой энергии на динамику Вселенной. Дополнительные слагаемые описывают источники сил отталкивания.

. Результаты (продолжение 1)
Записаны обобщенные космологические уравнения А.А.Фридмана в которых космологические силы отталкивания могут быть связаны с тепловой энергией космической среды.
Показано, что предлагаемым нами методом могут быть описаны эйнштейновские силы отталкивания (Λ-член).
Показано, что природу космологических сил отталкивания можно объяснить не вводя дополнительных гипотетических сред с отрицательным давлением. Есть основания считать, что источником этих сил является тепловая энергия космической среды.

. Результаты (продолжение 2)
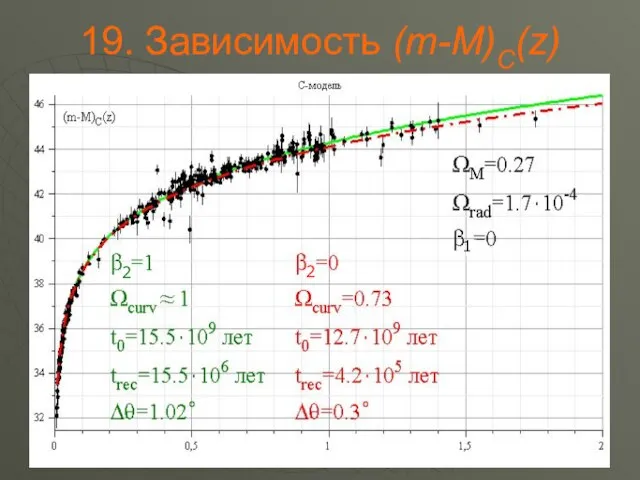
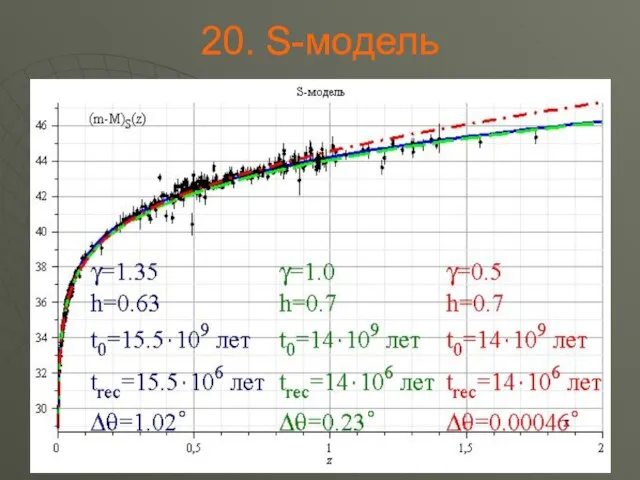
Предложены космологические модели однородной изотропной Вселенной, основанные на «тепловой природе» космологических сил отталкивания (C- и S- модели).
Доказана способность предлагаемых космологических моделей правильно объяснять важные наблюдения, в которых влияние космологического расширения является существенным.

. Результаты (продолжение 3)
В рамках C- и S- моделей дано объяснение возраста Вселенной;
Приведена интерпретация наблюдаемой зависимости «видимая звездная величина – красное смешение» для сверхновых типа Ia;
Объяснено наблюдаемое угловое расстояние между центрами соседних пятен на равномерном фоне реликтового излучения.