Обобщающий урок по теме «Функция»

Нет ни одной области математики, как бы абстрактна она не была, которая когда-нибудь не окажется применимой к явлениям действительного мира.
Н.И. Лобачевский

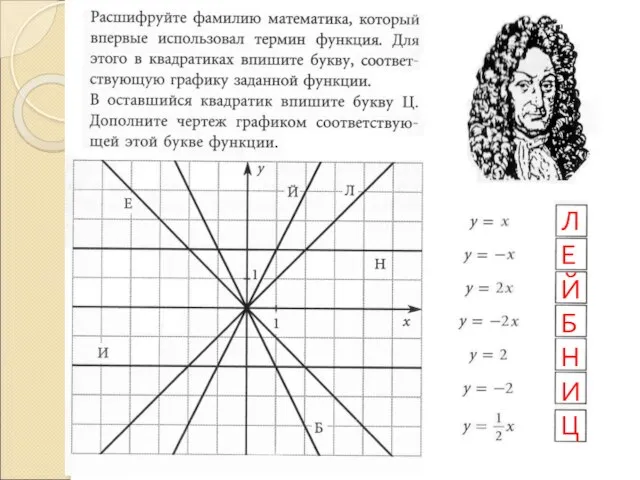
Множество точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты- соответствующим значениям функции называется функции
- это равенство, содержащее переменную, значение которой необходимо найти
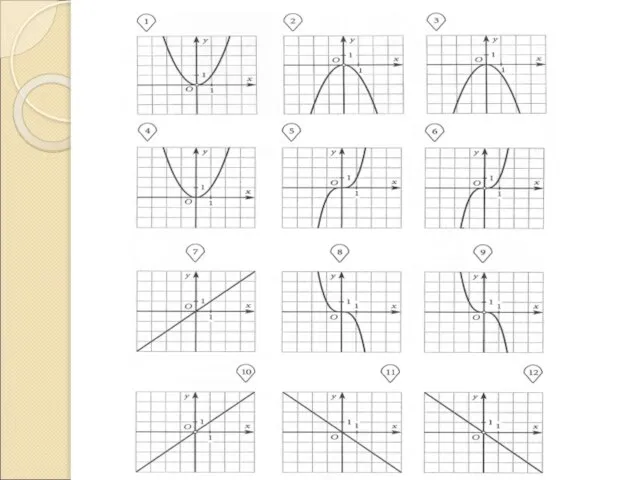
Функция вида y=хn,где х- независимая переменная, а n- натуральное число, называют функцией с натуральным показателем
уравнения называют значение переменной, при котором уравнение обращается в верное числовое равенство
График функции вида y=x3 обладает симметрией
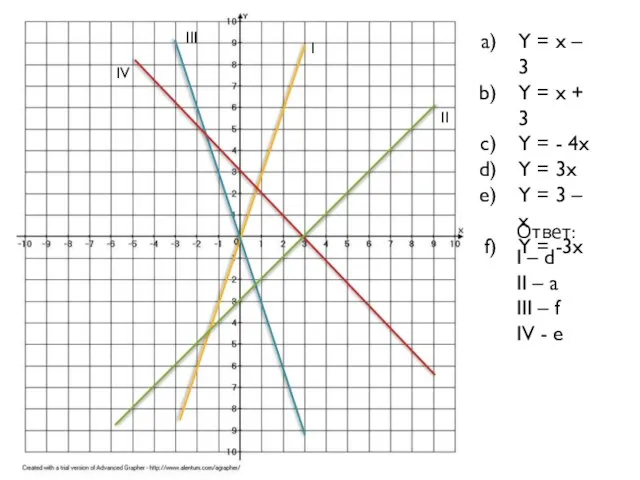
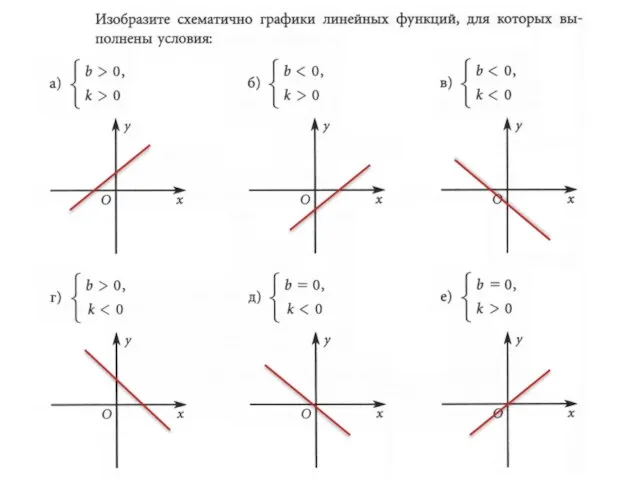
Функция, которая задается формулой вида y=kx+b, где х- независимая переменная, k и b – любые числа, называется функцией
Графиком линейной функции является
графиком
Уравнение
степенной
Корнем
центральной
линейной
прямая

Тема урока
«Обобщающий урок по теме «Функция»»

Л
Е
Й
Б
Н
И
Ц

Виды функций
Функция прямой пропорциональности
Линейная функция
Степенная функция
Y = kx , х – независимая переменная, к≠0
Y = kx+b, х – независимая переменная,
k и b - любые
Y = xn , х – независимая переменная,
n -натуральное

I
II
III
IV
Y = x – 3
Y = x + 3
Y = - 4x
Y = 3x
Y = 3 – x
Y = -3x
Ответ:
I – d
II – a
III – f
IV - e

Х - любое
Х - любое
Х - любое
Х - любое
Х - любое
Х ≠ 0
Х ≠ 0
Х ≠ 0
Х ≠ 0
Х ≠ 0
4
5
3
4
1
8
10
12
10
9

Домашнее задание
№ 1148 (б,г)
№ 1165
№ 1178 (б,г)