Содержание
- 2. Пример После проведения социологического исследования, как выявить группы людей сходных мнений? Есть большая база данных изображений,
- 3. Обучение без учителя Пусть, имеется набор наблюдений: Требуется некоторым образом сделать суждения о наблюдаемых данных Трудно
- 4. Обучение без учителя Кластеризация Разбиение наблюдений на некоторые группы, с максимально близкими наблюдениями внутри групп и
- 5. Обучение без учителя Кластеризация К-средних Смесь нормальных распределений … Понижение размерности Метод главных компонент SOM …
- 6. Отличие от классификации Множество ответов неизвестно Нет четкой меры качества решений Задачи поставлены крайне нечетко
- 7. Кластеризация Постановка задачи (1) Пусть, имеется набор наблюдений: Требуется разбить на некоторые непересекающиеся подмножества (группы, кластеры),
- 8. Кластеризация Постановка задачи (2) Пусть, так же, имеется некоторая мера , характеризующая «схожесть» между объектами Тогда,
- 9. Кластеризация Модель кластеров Под моделью кластеров будем понимать некоторое параметрическое семейство отображений из исходного пространства в
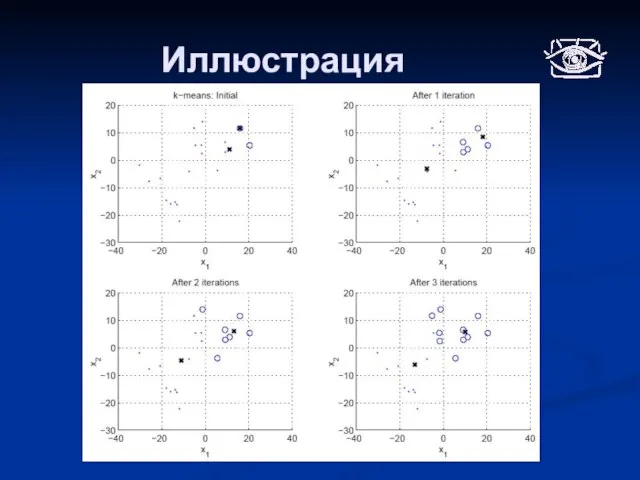
- 10. Алгоритм К-средних Кто хочет рассказать как он работает? Случайным образом выбрать k средних mj j=1,…,k; Для
- 11. Иллюстрация
- 12. Алгоритм К-средних Мера схожести Евклидово расстояние в пространстве Х Модель кластеров Пространство поиска - центры масс
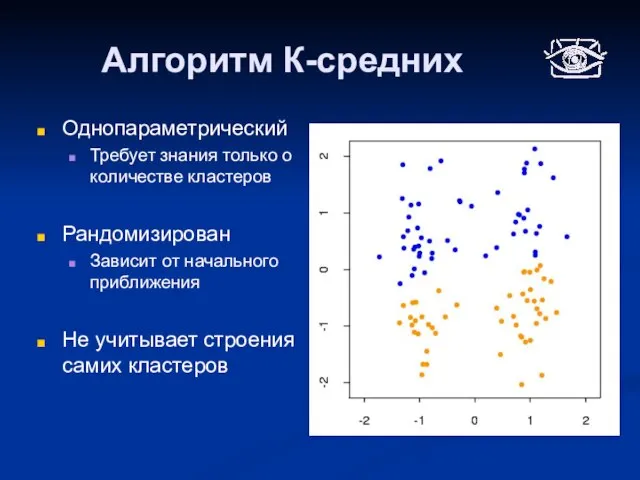
- 13. Алгоритм К-средних Однопараметрический Требует знания только о количестве кластеров Рандомизирован Зависит от начального приближения Не учитывает
- 14. EM алгоритм Общая идеология Пусть есть вектор неизвестных величин и параметрическая модель с так же неизвестным
- 15. EM алгоритм Общая идеология Возьмем некоторые начальные приближения Итеративно t =1… делаем два шага: Expect: согласно
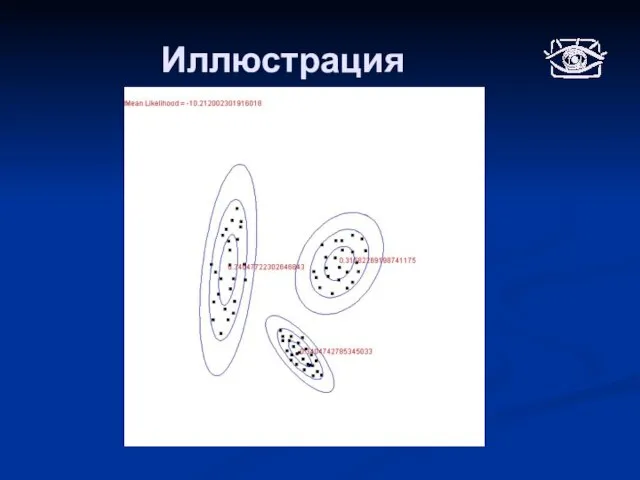
- 16. Кластеризация смесью нормальных распределений Будем считать, что наблюдения сгенерированы смесью нормальных распределений, то есть: Пусть k
- 17. Кластеризация смесью нормальных распределений Возьмем некоторые (случайные) начальные приближения Итеративно для t =1… : E: согласно
- 18. Иллюстрация
- 19. Кластеризация смесью нормальных распределений Плюсы Более полная модель кластеров (больше итоговой информации) Более качественная аппроксимация Эффективная
- 20. Иллюстрация
- 21. Понижение размерности наблюдаемых данных Зачастую, наблюдаемые данные могут обладать высокой размерностью, но в действительности быть функцией
- 22. Метод главных компонент Пусть имеется набор наблюдений Будем строить новый базис в пространстве , таким образом
- 23. Метод главных компонент Расчет базиса Сдвинем все данные таким образом, чтобы их выборочное среднее равнялось нулю
- 24. Метод главных компонент Расчет базиса Векторами нового базиса будут являться собственные вектора ковариационной матрицы Собственные числа
- 25. Иллюстрация Убирая базисные вектора с малыми значениями мы можем сократить размерность без существенной потери информации *Вопрос:
- 26. Случай нормального распределения Расстояние от центра распределения в новой системе координат равно: Так называемое расстояние Махалонобиса
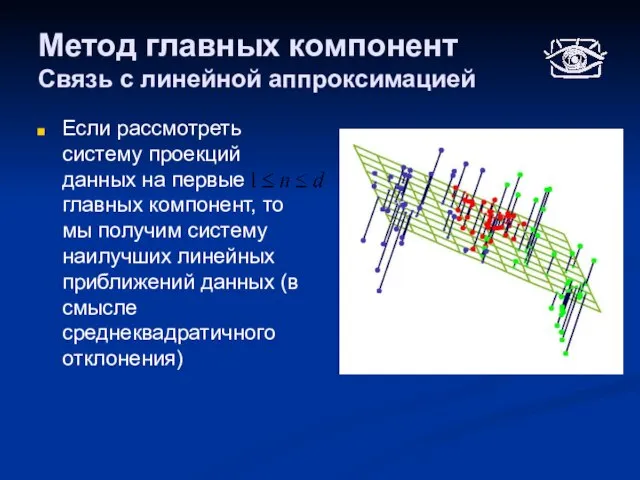
- 27. Метод главных компонент Связь с линейной аппроксимацией Если рассмотреть систему проекций данных на первые главных компонент,
- 28. Метод главных компонент Следует применять: Данные распределены нормально и требуется привести их к более удобной форме
- 29. Самоорганизующиеся карты SOM (Карты Кохенена) Основная идея вписать в данные сетку низкой размерности, и анализировать ее,
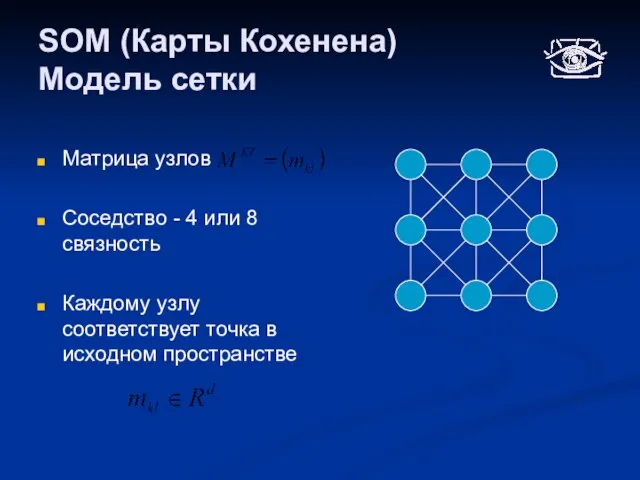
- 30. SOM (Карты Кохенена) Модель сетки Матрица узлов Соседство - 4 или 8 связность Каждому узлу соответствует
- 31. SOM (Карты Кохенена) Алгоритм построения Проинициализируем случайными значениями Далее, в случайном порядке будем предъявлять наблюдения и
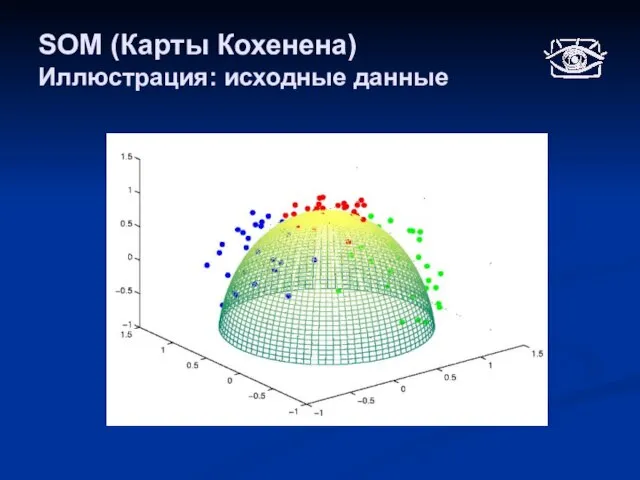
- 32. SOM (Карты Кохенена) Иллюстрация: исходные данные
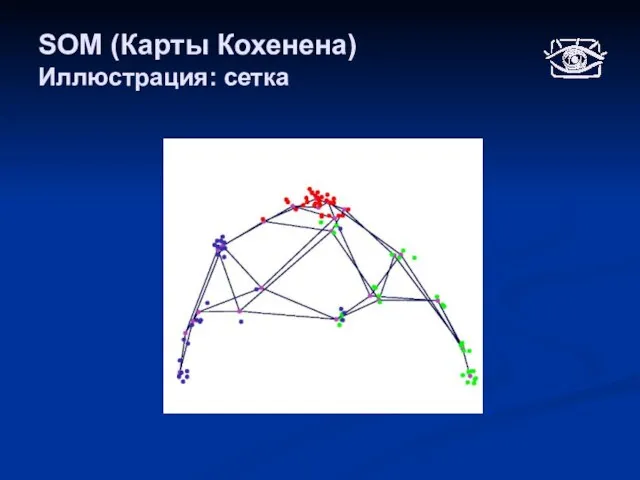
- 33. SOM (Карты Кохенена) Иллюстрация: сетка
- 34. SOM (Карты Кохенена) Иллюстрация: проекции на матрицу
- 35. SOM (Карты Кохенена) Практическое использование Данные представляют некоторую поверхность, требуется сократить размерность Хорошо подходят для последующей
- 36. Задание №2 Каждому будут выданы Данные (3 набора) Алгоритмы классификации, реализованные в MatLab Требуется Для каждого
- 37. Содержание отчета Применявшиеся методы Список Алгоритм, по которому оценивались алгоритмы и выбирались параметры Результаты в виде
- 39. Скачать презентацию





























 Реализация проекта Мой бизнес в Нижегородской области
Реализация проекта Мой бизнес в Нижегородской области 3D модель анемометра из алюминиевого сплава с защитным керамическим покрытием
3D модель анемометра из алюминиевого сплава с защитным керамическим покрытием Present Perfect 8 class
Present Perfect 8 class Животные пустыни
Животные пустыни Михаил Афанасьевич Булгаков (1891-1940) Жизнь и творчество
Михаил Афанасьевич Булгаков (1891-1940) Жизнь и творчество Мир человеческих чувств. Практическая работа. 8 класс
Мир человеческих чувств. Практическая работа. 8 класс Лекция 1. Проектирование плана и продольного профиля автомобильной дороги
Лекция 1. Проектирование плана и продольного профиля автомобильной дороги Применение методов решения задачи удовлетворения ограничениям для построения управляющих конечных автоматов по сценариям работ
Применение методов решения задачи удовлетворения ограничениям для построения управляющих конечных автоматов по сценариям работ консультационные услуги по вопросам применения информационных технологий
консультационные услуги по вопросам применения информационных технологий Моделирование деятельности органов исполнительной власти как инструмент административной реформы
Моделирование деятельности органов исполнительной власти как инструмент административной реформы Серебряный век как своеобразие русского ренессанса
Серебряный век как своеобразие русского ренессанса 6 лет в эфире (начало работы 28 декабря 2002 г.); одна из самых популярных российских радиостанций; первое зауральское радио ( г. Курган и
6 лет в эфире (начало работы 28 декабря 2002 г.); одна из самых популярных российских радиостанций; первое зауральское радио ( г. Курган и Дождь
Дождь Здоровье дошкольников и пути его улучшения
Здоровье дошкольников и пути его улучшения Дипломный проект. Реконструкция системы электроснабжения центрального района г. Заозерного
Дипломный проект. Реконструкция системы электроснабжения центрального района г. Заозерного Псевдо-конфликт. Факт-конфликт. Эго-конфликт
Псевдо-конфликт. Факт-конфликт. Эго-конфликт Мой адрес в мире
Мой адрес в мире Отношение россиян к участию Российской Федерации в оказании помощи развивающимся странам
Отношение россиян к участию Российской Федерации в оказании помощи развивающимся странам С днем Победы. Шаблон
С днем Победы. Шаблон Сенсорная комната как средство развития коммуникативных возможностей и способностей.
Сенсорная комната как средство развития коммуникативных возможностей и способностей. Формирование Древнерусского государства
Формирование Древнерусского государства Концертный зал им. И.Шакирова
Концертный зал им. И.Шакирова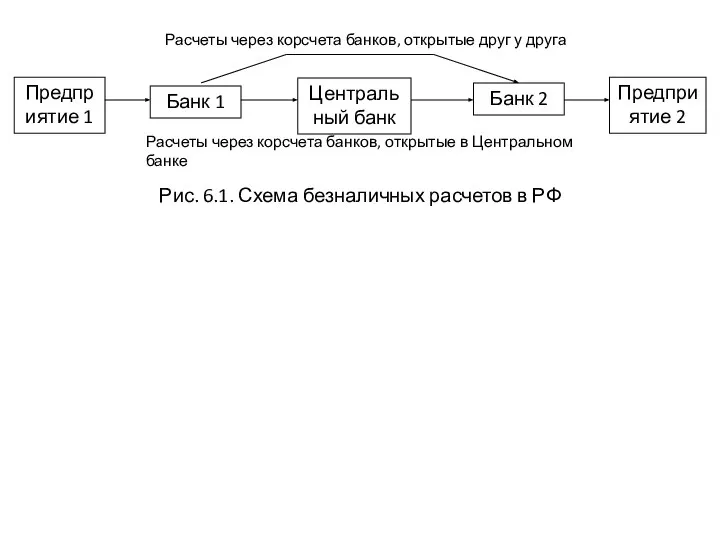 Безнал. Расчеты через корсчета банков
Безнал. Расчеты через корсчета банков Здоровые зубы, счастливый человек. Зубная паста для здоровья и блеска зубов Orecare
Здоровые зубы, счастливый человек. Зубная паста для здоровья и блеска зубов Orecare Производственная сигнализация при выполнении такелажных работ
Производственная сигнализация при выполнении такелажных работ Социальная структура
Социальная структура Chanel Allure Homme sport Cologne
Chanel Allure Homme sport Cologne Герои сказки глазами художника
Герои сказки глазами художника