Содержание
- 2. Обыкновенные дифференциальные уравнения Обыкновенным дифференциальным уравнением называется уравнение, связывающее между собой значения независимой переменной x, неизвестной
- 3. ОДУ первого порядка Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида: где x - независимая переменная,
- 4. Разделяют несколько типов (видов) обыкновенных дифференциальных уравнений: -Уравнения с разделяющимися переменными, -Однородные уравнения, -Линейные уравнения, -Уравнение
- 5. Уравнения с разделёнными переменными. Так называются уравнения вида удовлетворяющее начальному условию f(x)dx + g(y)dy = 0,
- 6. Уравнения с разделяющимися переменными. Так называются уравнения вида Эти уравнения легко сводятся к уравнению с разделёнными
- 7. Выразим у из последнего выражения как функцию х, получим общее решение: Пример:
- 8. Уравнения с однородной правой частью. Так называются уравнения со специальным видом зависимости функции f(x, y) от
- 9. Пример: - общее решение уравнения
- 10. Окончательно, получим общее решение: Пример:
- 11. Линейные уравнения. ДУ первого порядка называется линейным, если неизвестная функция y(x) и её производная входят в
- 12. Для решения уравнения представим y(x) в виде произведения двух новых неизвестных функций u(x) и v(x): y(x)
- 13. Отметим, решая уравнение на v(x) мы не вводим в это решение произвольную постоянную C, нам достаточно
- 14. Пример: Решение: и общее решение уравнения .
- 15. Для нахождения частного решения, соответствующего начальным условиям (задача Коши), подставим в общее решение Решение задачи:
- 16. Уравнение в полных дифференциалах. Так называется уравнение вида (P(x, y), Q(x, y) - непрерывно дифференцируемы) в
- 17. Для нахождения функции u(x, y) решается система уравнений Из первого уравнения этой системы находим: с точностью
- 18. Пример: найти общее решение уравнения Убедимся, что это - уравнение в полных дифференциалах. .
- 19. Задание: К какому типу относятся дифференциальные уравнения:
- 21. ОДУ высших порядков Обыкновенным дифференциальным уравнением называется уравнение, связывающее между собой значения независимой переменной x, неизвестной
- 22. Некоторые типы уравнений, допускающие понижение порядка. Уравнение вида решается последовательным n-кратным интегрированием. Переобозначив постояные, общее решение
- 23. Уравнение, не содержащее в явном виде неизвестную функцию и её младшие производные. Порядок уравнения вида F(x,
- 24. Пример: Понизить порядок уравнения: Младшая производная, входящая в явной форме в уравнения, - вторая, поэтому делаем
- 25. Уравнение, не содержащее в явном виде независимую переменную x. Порядок уравнения не содержащего явно x, может
- 27. Скачать презентацию


















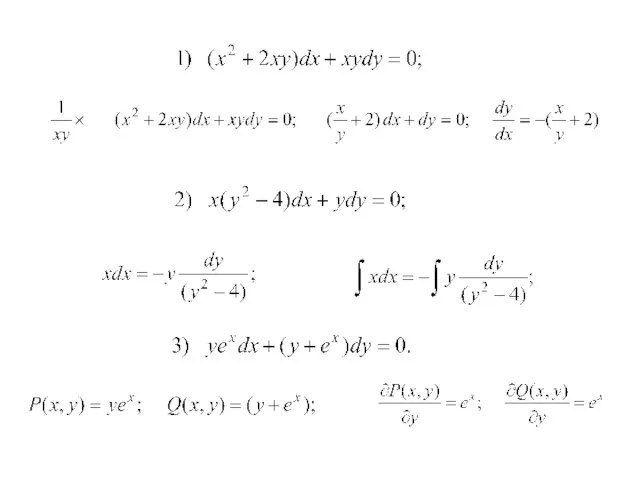





 Обособление приложений
Обособление приложений Кто такие звери?
Кто такие звери? ГЛАВНЫЙ ПРОДУКТ
ГЛАВНЫЙ ПРОДУКТ Национальный центр искусства и культуры Жоржа Помпиду
Национальный центр искусства и культуры Жоржа Помпиду Доказательства происхождения человека от животных
Доказательства происхождения человека от животных Итоговое сочинение - 2018
Итоговое сочинение - 2018 Параллельность плоскостей 10 класс
Параллельность плоскостей 10 класс Лекция № 4
Лекция № 4 для Саши 20 лет
для Саши 20 лет Свободный, кросс-платформенный, основанный на стандартах, защищенный, современный, расширяемый, настраиваемый пакет приложений дл
Свободный, кросс-платформенный, основанный на стандартах, защищенный, современный, расширяемый, настраиваемый пакет приложений дл Подготовка к сочинению-рассуждению на лингвистическую тему
Подготовка к сочинению-рассуждению на лингвистическую тему Познание
Познание Ипотека с господдержкой 2020
Ипотека с господдержкой 2020 И помнит мир спасенный
И помнит мир спасенный лекція 2 кібербезпека для СВ 2022
лекція 2 кібербезпека для СВ 2022 Prezentatsia1
Prezentatsia1 Условия назначения, порядок выплаты и размеры компенсаций неработающим женам военнослужащих
Условия назначения, порядок выплаты и размеры компенсаций неработающим женам военнослужащих Российско- Финляндское приграничное сотрудничество
Российско- Финляндское приграничное сотрудничество Пространственное распределение живого
Пространственное распределение живого  Социальная инженерия
Социальная инженерия Яблоня – символ жизни, здоровья, красоты
Яблоня – символ жизни, здоровья, красоты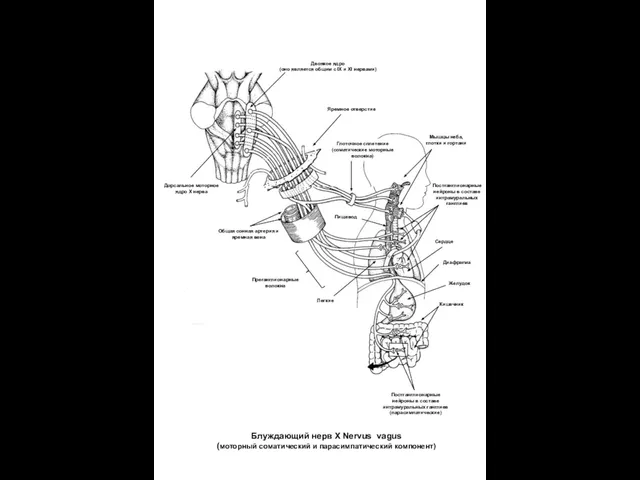 Двоякое ядро
Двоякое ядро OTHER ABBREVIATIONS
OTHER ABBREVIATIONS  Набросок фигуры человека с натуры
Набросок фигуры человека с натуры Смена дня и ночи 2 класс
Смена дня и ночи 2 класс Гражданский процесс
Гражданский процесс Презентация на тему: Письмо
Презентация на тему: Письмо Окружной конкурс на лучшее оформление здания образовательной организации к Новому году Новогодняя феерия
Окружной конкурс на лучшее оформление здания образовательной организации к Новому году Новогодняя феерия