Содержание
- 2. Лекция 4 Базисные средства манипулирования реляционными данными: реляционная алгебра Кодда 1. Обзор реляционной алгебры Кодда 2.
- 3. 1. Обзор реляционной алгебры Кодда Основная идея реляционной алгебры: поскольку отношения являются множествами, средства манипулирования отношениями
- 4. 1. Обзор реляционной алгебры Кодда Классы операций: А). Теоретико-множественные операции Б). Специальные реляционные операции объединение ограничение
- 5. Общая интерпретация реляционных операций При выполнении операции объединения (UNION) двух отношений с одинаковыми заголовками производится отношение,
- 6. Общая интерпретация реляционных операций Отношение - разность (MINUS) двух отношений с одинаковыми заголовками, включает все кортежи,
- 7. Общая интерпретация реляционных операций Результатом ограничения (WHERE) отношения по некоторому условию является отношение, включающее кортежи отношения-операнда,
- 8. Общая интерпретация реляционных операций При соединении (JOIN) отношений по некоторому условию образуется отношение, кортежи которого есть
- 9. Общая интерпретация реляционных операций Операция переименования (RENAME) производит отношение, тело которого совпадает с телом операнда, но
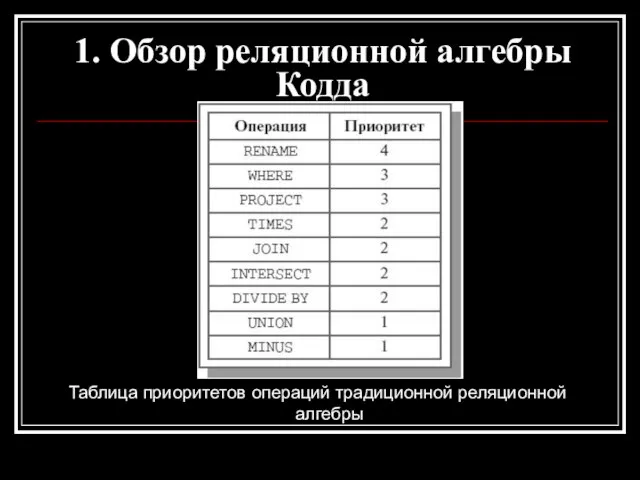
- 10. Таблица приоритетов операций традиционной реляционной алгебры 1. Обзор реляционной алгебры Кодда
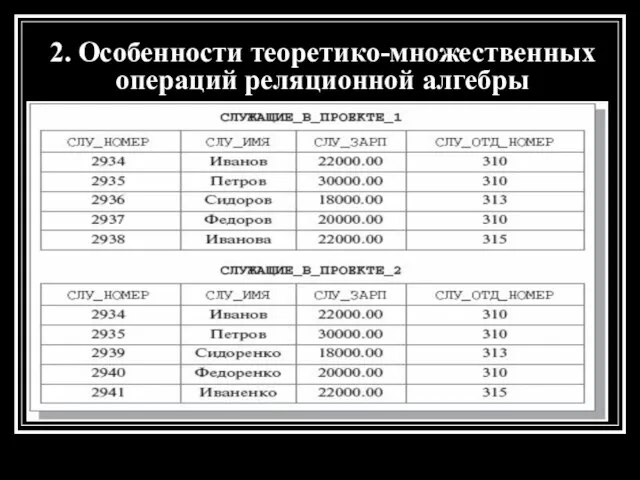
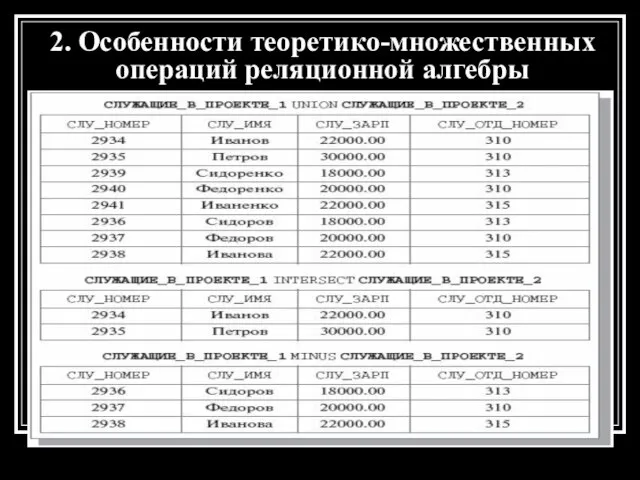
- 11. 2. Особенности теоретико-множественных операций реляционной алгебры
- 12. 2. Особенности теоретико-множественных операций реляционной алгебры
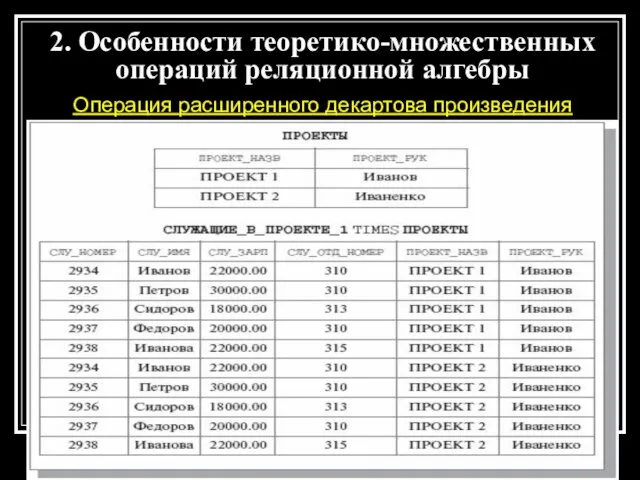
- 13. Операция расширенного декартова произведения элементом результирующего отношения является кортеж, который представляет собой объединение одного кортежа первого
- 14. Операция расширенного декартова произведения Пусть имеются два отношения R1{a1, a2, …, an} и R2{b1, b2, …,
- 15. Операция расширенного декартова произведения 2. Особенности теоретико-множественных операций реляционной алгебры
- 16. вид1 (a comp-op b), где а и b – имена атрибутов ограничиваемого отношения вид2 (a comp-op
- 17. A WHERE (comp1 AND comp2) обозначает то же самое, что и (A WHERE comp1) INTERSECT (A
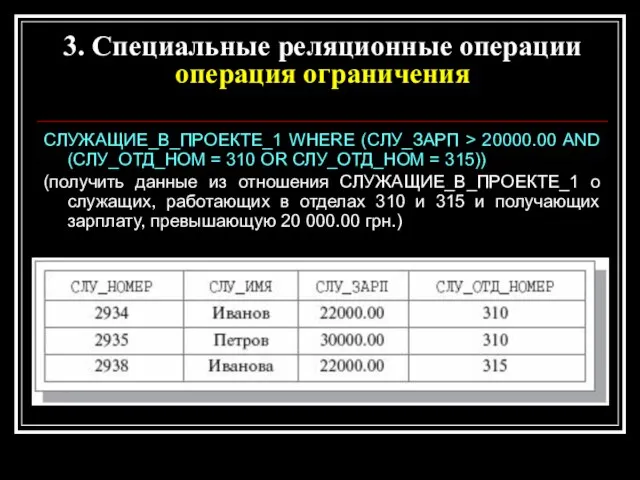
- 18. СЛУЖАЩИЕ_В_ПРОЕКТЕ_1 WHERE (СЛУ_ЗАРП > 20000.00 AND (СЛУ_ОТД_НОМ = 310 OR СЛУ_ОТД_НОМ = 315)) (получить данные из
- 19. Результатом проекции отношения A на множество атрибутов {a1, a2, ..., an} (PROJECT A {a1, a2, ...,
- 20. Результат операции PROJECT СЛУЖАЩИЕ_В_ПРОЕКТЕ_1 {СЛУ_ОТД_НОМ} (в каких отделах работают служащие, данные о которых содержатся в отношении
- 21. 3. Специальные реляционные операции операция соединения Разновидности: Общая операция соединения Θ - соединение (тэта-соединение) Экви-соединение Естественное
- 22. Соединением отношений А и В по условию С называется отношение С - логическое выражение, в которое
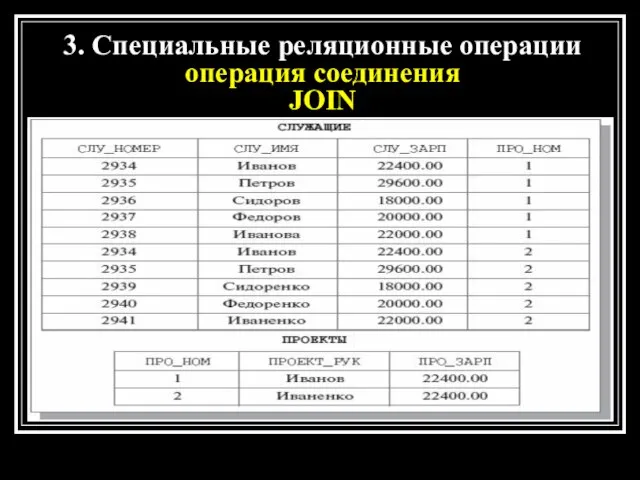
- 23. 3. Специальные реляционные операции операция соединения JOIN
- 24. Результат операции СЛУЖАЩИЕ JOIN ПРОЕКТЫ WHERE (СЛУ_ЗАРП > ПРО_ЗАРП) 3. Специальные реляционные операции операция соединения JOIN
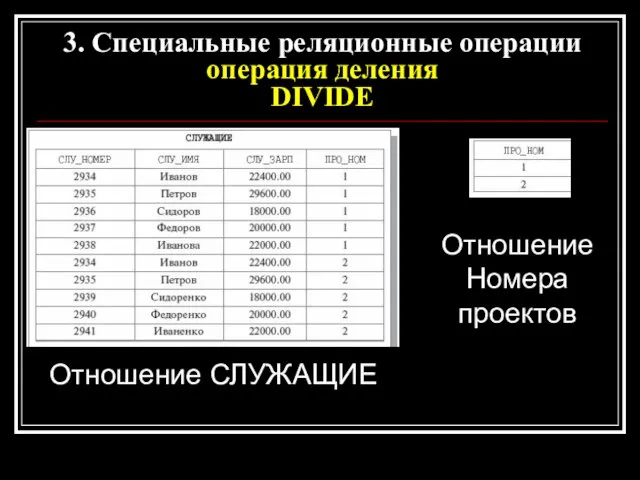
- 25. Отношение СЛУЖАЩИЕ 3. Специальные реляционные операции операция деления DIVIDE Отношение Номера проектов
- 27. Скачать презентацию

















 Электромобиль как распределенный накопитель энергии
Электромобиль как распределенный накопитель энергии Совершенствование эксплуатации МПП с модернизацией пропашного культиватора
Совершенствование эксплуатации МПП с модернизацией пропашного культиватора Стратегия продвижения социальной миссии Domestos
Стратегия продвижения социальной миссии Domestos Литературная викторина по повести Н. В. Гоголя «Тарас Бульба»
Литературная викторина по повести Н. В. Гоголя «Тарас Бульба» 3. Классификация ПК
3. Классификация ПК Наши права. Основные права потребителей
Наши права. Основные права потребителей Банковский счет
Банковский счет Глобальная угроза международного терроризма. Пути решения
Глобальная угроза международного терроризма. Пути решения Краснодарский архитектурно-строительный техникум
Краснодарский архитектурно-строительный техникум с эстетическими направлениями
с эстетическими направлениями Этикет в японской семье: от традиций к современностям
Этикет в японской семье: от традиций к современностям Шаг навстречу
Шаг навстречу Русская философия
Русская философия  Шолохов
Шолохов Презентация на тему Жизненные формы растений
Презентация на тему Жизненные формы растений Инфабрика. Первый частный музей современного сибирского искусства
Инфабрика. Первый частный музей современного сибирского искусства Занимательный русский язык
Занимательный русский язык Угол. Виды углов
Угол. Виды углов «Тип Членистоногие»
«Тип Членистоногие» Пенсионное обеспечение
Пенсионное обеспечение Дед Мороз
Дед Мороз Cash on Card Наличные за 15 минут_9
Cash on Card Наличные за 15 минут_9 Мягкая мебель собственного производства
Мягкая мебель собственного производства День Конституции РФ
День Конституции РФ Презентация на тему Что где когда по ПДД
Презентация на тему Что где когда по ПДД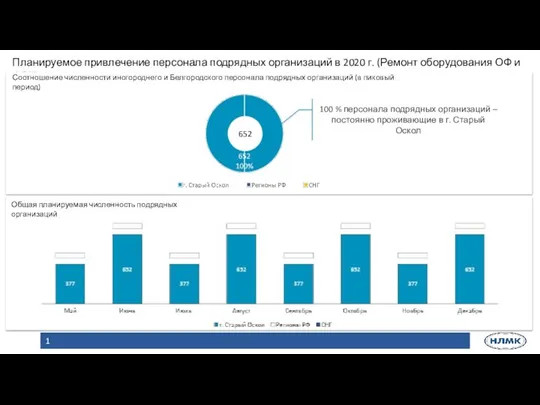 Подрядчики СГОК-v2
Подрядчики СГОК-v2 Дашинима Бальжанович Намдаков
Дашинима Бальжанович Намдаков Выбор и моделирование двигателя постоянного тока для скоростного следящего электропривода
Выбор и моделирование двигателя постоянного тока для скоростного следящего электропривода