Слайд 3План
Computer Science
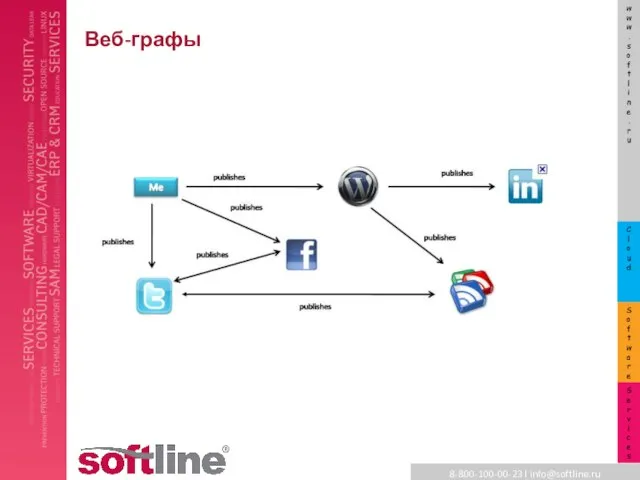
Web-графы
Случайные графы
Highway dimenstion
NP vs P
Что осталось нерассмотренным
Послесловие

Слайд 12Computer Science
Закон Вирта
Программы становятся медленне более быстро, чем компьютеры становятся быстрее
P =

A =
Mρ - множество процедур решения задачи
R2 ⊂ Mρ ² - бинарное отношение на Mρ
(ρi, ρj) ∈ R2 ⇔ после пройедуры ρi выполняется процедура ρj
Слайд 15Теория графов + Теория вероятностей = PROFIT
+

Слайд 18Случайные графы
Наблюдения Барабаши-Альберт
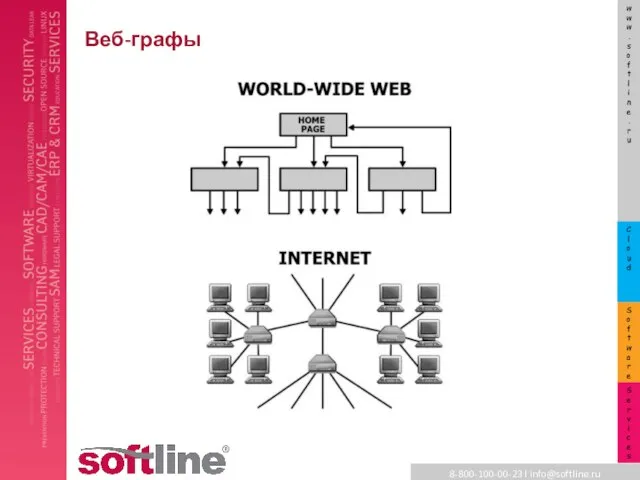
Как устроен web-граф?
Barabashi, Albert, 1999, 2000
5 млрд вершин, псевдомультиорграф
Ключевые свойства

веб-графа:
∙ Разрежённость
на k вершин kt рёбер, k ≥ 1
∙ Диаметр графа ∈ {5, 6}
Теория о шести рукопожатиях
∙ Степенное распределение степеней вершин
P(d) ~ c / d λ
λ ≈ 2.1, c – нормирующий множитель
Слайд 19Случайные графы
Наблюдения Барабаши-Альберт
Веб-граф очень специфичен – разрежен и тесен
Степенной закон объединяет социальные,
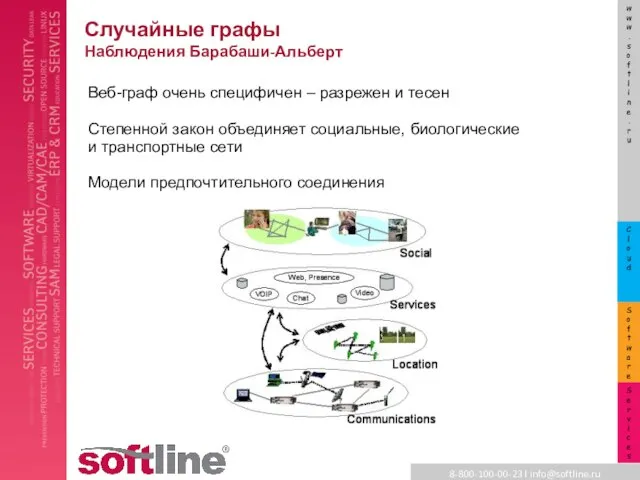
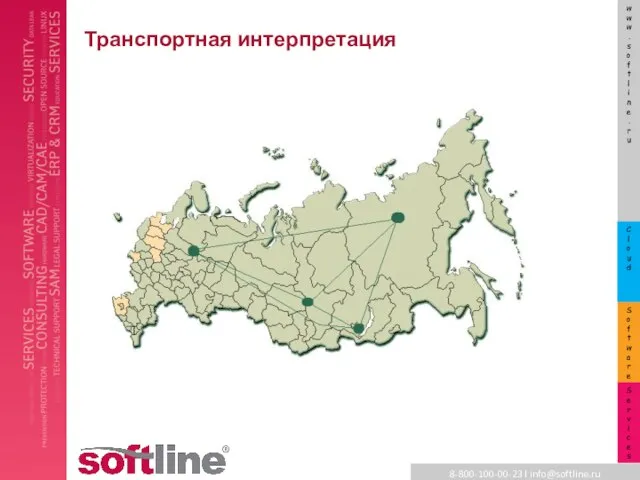
биологические и транспортные сети
Модели предпочтительного соединения
Слайд 20Случайные графы
Модель Эрдёша-Реньи
G(n,p)
V = {1, 2, …, n}, E
рёбра проводятся взаимно-независимо с
вероятностью

p ∈ [0, 1] в соответствии со
схемой Бернулли
e1, …, em, m = C2n – количество всех испытаний
Вероятностное пространство <Ωn, Fn, Pn,p>
Ωn = {G = (Vn, E)} – множество элементарных событий
Fn = 2Ωn – множество событий
Pn,p(G) = p|E|(1-p)m-|E| - вероятность повления конкретного графа
Слайд 23Highway dimension
Почему современные алгоритмы на картах работают очень быстро
100000 млн вершин
Время работы

10-2 c
Интуитивные идеи:
Указатели на дугах
Поиск A*
Достижимость
Шоссейная и желаемые иерархии
Перевалочные пункты
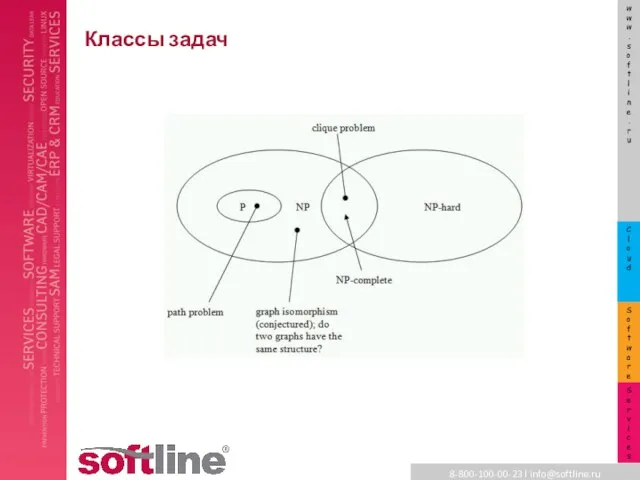
Слайд 27P vs NP
Задача поиска задаётся алгоритмом C, который получает на вход условие

I и кандидата на решение S и имеет полиномиальное, относительно I время работы.
S называется решением если и только если C(S, I) = true
NP – класс всех задач поиска, решение для которых может быть быстро проверено
P – класс задач поиска, решение для которых может быть быстро найдено
P ≠ NP – верно ли, что каждый раз, когда решение можно быстро проверить, его можно быстро найти
Задача о расписании
Задача о вершинном покрытии
A → B
Слайд 30Что осталось нерассмотренным
Параллельные алгоритмы
Распознавание изображений
Нейронные сети
Генетические алгоритмы
Нечёткие модели
Строковые алгоритмы
Комбинаторная оптимизация
Численные алгоритмы
Вычислительная геометрия
Криптографические

алгоритмы
Компьютерная лингвистика
……..






















 Франция во второй половине XIX века
Франция во второй половине XIX века Влияние ребрендинга на финансовые результаты компании
Влияние ребрендинга на финансовые результаты компании [Группа 152]
[Группа 152] Экология и автомобиль
Экология и автомобиль Центр молодежной политики ГАУГН. Паспорт студента. Руководство пользования
Центр молодежной политики ГАУГН. Паспорт студента. Руководство пользования Интерфероны
Интерфероны Сухопутные войска (пехота, артиллерия, ракетные части, танки)
Сухопутные войска (пехота, артиллерия, ракетные части, танки) Антуан Монкретьн де Ваттевіль
Антуан Монкретьн де Ваттевіль Народная мораль в характере главных героев Л.Н.Толстого «Старый дед и внучек»
Народная мораль в характере главных героев Л.Н.Толстого «Старый дед и внучек» ПЕРВАЯЛЮБОВЬсвежесть отношений
ПЕРВАЯЛЮБОВЬсвежесть отношений Воспитательные технологии: от КТД до тренингов. Резервные возможности использования дискуссионных, проблемных методов в современ
Воспитательные технологии: от КТД до тренингов. Резервные возможности использования дискуссионных, проблемных методов в современ Ионный двигатель с СВЧ ионизацией
Ионный двигатель с СВЧ ионизацией Химические раскопки по классам неорганических соединений
Химические раскопки по классам неорганических соединений Понятие конфликта. (Урок 3)
Понятие конфликта. (Урок 3) Внешняя политика Россиив начале XIX века
Внешняя политика Россиив начале XIX века Мой магазин Настольных игр
Мой магазин Настольных игр EA-OD19
EA-OD19 Презентация на тему Средневековый город и его обитатели 6 класс
Презентация на тему Средневековый город и его обитатели 6 класс  Имидж делового человека
Имидж делового человека Общепринятая структура научного текста
Общепринятая структура научного текста Loving Hut. Контент-план
Loving Hut. Контент-план ПРЕЗЕНТАЦИЯ Новосибирск 2009 г.
ПРЕЗЕНТАЦИЯ Новосибирск 2009 г. БИРЖЕВЫЕ НОВОСТИ –КАКИМИ ИМ БЫТЬ?На примере распространения информации Казахстанской фондовой биржей (KASE)
БИРЖЕВЫЕ НОВОСТИ –КАКИМИ ИМ БЫТЬ?На примере распространения информации Казахстанской фондовой биржей (KASE) Варианты покраски
Варианты покраски Три девицы под окном
Три девицы под окном Возможности продвижения тиражируемых продуктов
Возможности продвижения тиражируемых продуктов Этнокультурный компонент в технологическом образовании как средство познания мира
Этнокультурный компонент в технологическом образовании как средство познания мира СМС дети УЛЫБКА. Здоровая пробежка
СМС дети УЛЫБКА. Здоровая пробежка