Одномерная регрессионная модель Многомерная регрессионная модель

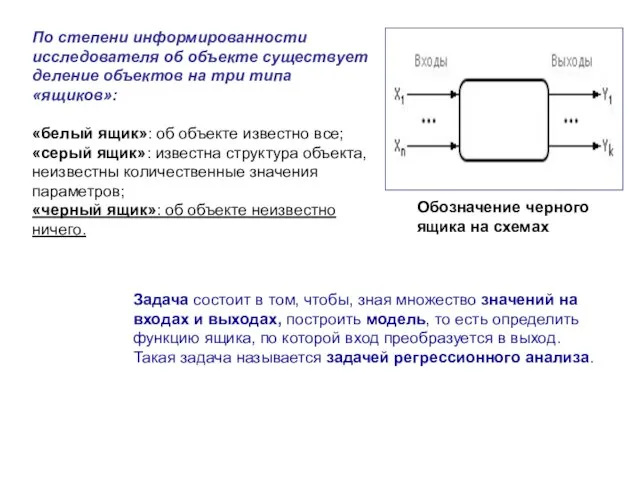
По степени информированности исследователя об объекте существует деление объектов на три типа «ящиков»:
«белый ящик»: об объекте известно все;
«серый ящик»: известна структура объекта, неизвестны количественные значения параметров;
«черный ящик»: об объекте неизвестно ничего.
Задача состоит в том, чтобы, зная множество значений на входах и выходах, построить модель, то есть определить функцию ящика, по которой вход преобразуется в выход. Такая задача называется задачей регрессионного анализа.
Обозначение черного ящика на схемах

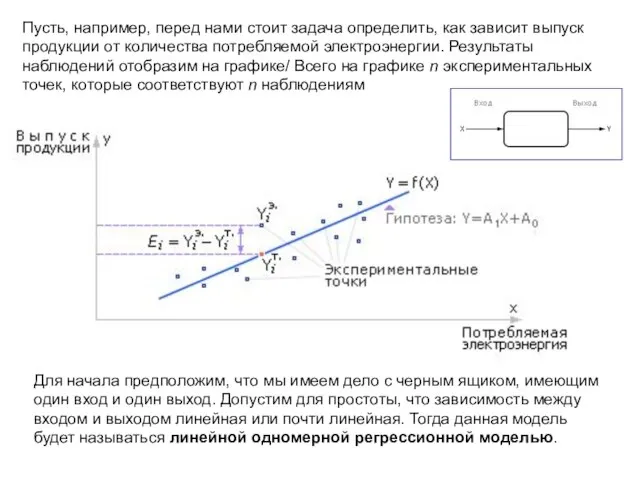
Пусть, например, перед нами стоит задача определить, как зависит выпуск продукции от количества потребляемой электроэнергии. Результаты наблюдений отобразим на графике/ Всего на графике n экспериментальных точек, которые соответствуют n наблюдениям
Для начала предположим, что мы имеем дело с черным ящиком, имеющим один вход и один выход. Допустим для простоты, что зависимость между входом и выходом линейная или почти линейная. Тогда данная модель будет называться линейной одномерной регрессионной моделью.

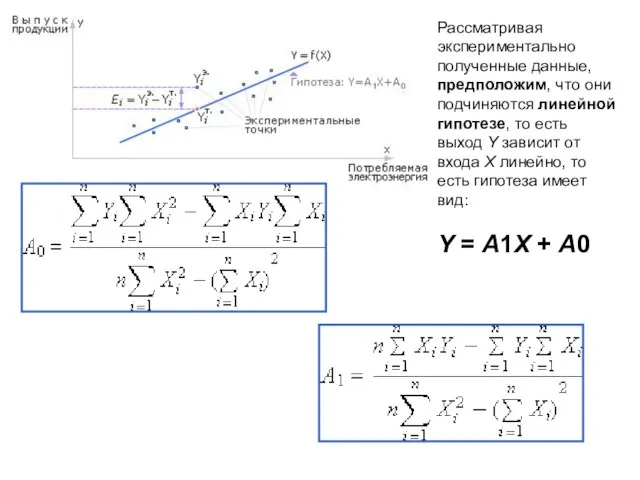
Рассматривая экспериментально полученные данные, предположим, что они подчиняются линейной гипотезе, то есть выход Y зависит от входа X линейно, то есть гипотеза имеет вид:
Y = A1X + A0

Проверка линейной гипотезы
Чтобы определить, принимается гипотеза или нет, нужно, во-первых, рассчитать ошибку между точками заданной экспериментальной и полученной теоретической зависимости и суммарную ошибку:
Ei = (YiЭксп. – YiТеор.), i = 1, …, n
n-общее
число точек
Если в полосу, ограниченную 2σ попадает 68.26% и более экспериментальных точек то выдвинутая гипотеза принимается. В противном случае выбирают более сложную гипотезу или проверяют исходные данные. Если требуется большая уверенность в результате, то используют дополнительное условие: в полосу, ограниченную линиями 4σ, должны попасть 95.44% и более экспериментальных точек.

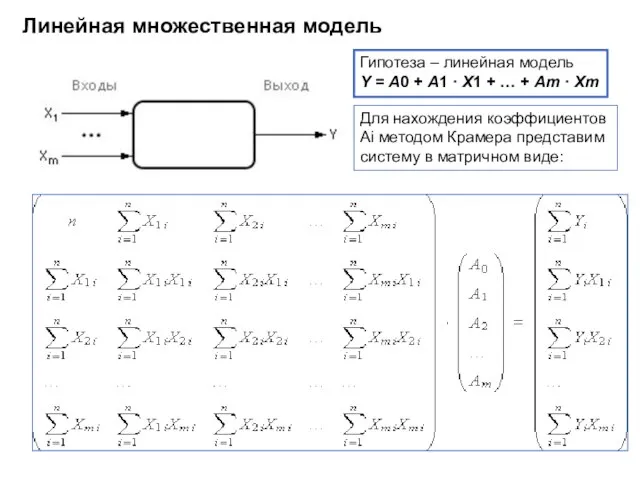
Линейная множественная модель
Гипотеза – линейная модель
Y = A0 + A1 · X1 + … + Am · Xm
Для нахождения коэффициентов Ai методом Крамера представим систему в матричном виде: