Слайд 2Линейный поиск.
Алгоритм.
Последовательно просматриваем массив
и сравниваем значение очередного элемента с данным, если

значение очередного элемента совпадет с Х, то запоминаем его номер в переменной k.
For i := 1 to n do if a[i] = x then k := i;
Недостатки данной реализации алгоритма:
находим только последнее вхождение элемента
в любом случае производится n сравнений
Слайд 3
Улучшим: будем прерывать поиск, как только найдем элемент:
while (i <= n )

and ( a[i] <> x) do inc(i);
В результате или найдем нужный элемент, или просмотрим весь массив.
Недостаток данной реализации:
в заголовке цикла сложное условие, что замедляет поиск.
Слайд 4 Бинарный поиск
Применяется для отсортированных массивов!!!!!!!.

Слайд 5Алгоритм
Является ли Х средним элементом массива. Если да, то поиск завершен,

иначе переходим к пункту 2.
Возможно 2 случая:
Х меньше среднего, тогда так как А упорядочен, то из рассмотрения можно исключить все элементы массива, расположенные правее среднего и применить метод к левой половине массива.
Х больше среднего. Значит, исключаем из рассмотрения левую половину массива и применяем метод к правой части.
Слайд 6begin
l := 1; r := n; {на первом шаге рассматриваем весь

массив}
f := false; {признак того, что Х не найден}
while ( l <= r ) and not f do
begin
m := (l+r) div 2;
if a[m] =x then f := true {элемент найден! Поиск прекращаем}
else if x < a[m] then r:=m-1 {отбрасываем правую часть}
else l := m + 1 {отбрасываем левую часть}
end;





 Общественно-активная школа: эффективность и качество.
Общественно-активная школа: эффективность и качество. 197368
197368 С какво свързваш древногръцкото облекло?
С какво свързваш древногръцкото облекло? Презентация на тему Экономика и ее роль в обществе
Презентация на тему Экономика и ее роль в обществе Фотоальбом. Велосипеди
Фотоальбом. Велосипеди Узорочья Севера
Узорочья Севера Цветы для моей семьи
Цветы для моей семьи Открытые горные работы, их элементы и терминология
Открытые горные работы, их элементы и терминология Бизнес инсайт. Продуктивность как система
Бизнес инсайт. Продуктивность как система Где летит птица?
Где летит птица? Итоги 1 полугодия 2010-2011 уч.года
Итоги 1 полугодия 2010-2011 уч.года Творческий проект Кукла своими руками
Творческий проект Кукла своими руками Буквы О-Ё после шипящих и Ц
Буквы О-Ё после шипящих и Ц Формы взаимодействия с семьей (из опыта работы)
Формы взаимодействия с семьей (из опыта работы) КОММУНИКАТИВНАЯ ПОЛИТИКА ХОЛДИНГОВ
КОММУНИКАТИВНАЯ ПОЛИТИКА ХОЛДИНГОВ Государственное регулирование цен на лекарственные средства на региональном уровне и проблемы, возникающие в рамках действующег
Государственное регулирование цен на лекарственные средства на региональном уровне и проблемы, возникающие в рамках действующег Презентация прочитанной книги
Презентация прочитанной книги Филиал ООО компания Тензор. Сфера торгов
Филиал ООО компания Тензор. Сфера торгов Рекуперативный воздухонагреватель, с использованием жидких горючих отходов.
Рекуперативный воздухонагреватель, с использованием жидких горючих отходов. Интерактивно-аналитический онлайн-сервиса Калькулятор процедур
Интерактивно-аналитический онлайн-сервиса Калькулятор процедур Элла Фицджеральд - выдающаяся джазовая певица, актриса 1917-1996
Элла Фицджеральд - выдающаяся джазовая певица, актриса 1917-1996 Места на направление Товароведение
Места на направление Товароведение Праця неповнолітніх
Праця неповнолітніх Прямолинейное распространение света
Прямолинейное распространение света Документовед он-лайн сервис оформления документов Документы для регистрации общества с ограниченной ответственностью за 15 минут.
Документовед он-лайн сервис оформления документов Документы для регистрации общества с ограниченной ответственностью за 15 минут. Как правильно оформить презентацию и web-сайт?
Как правильно оформить презентацию и web-сайт?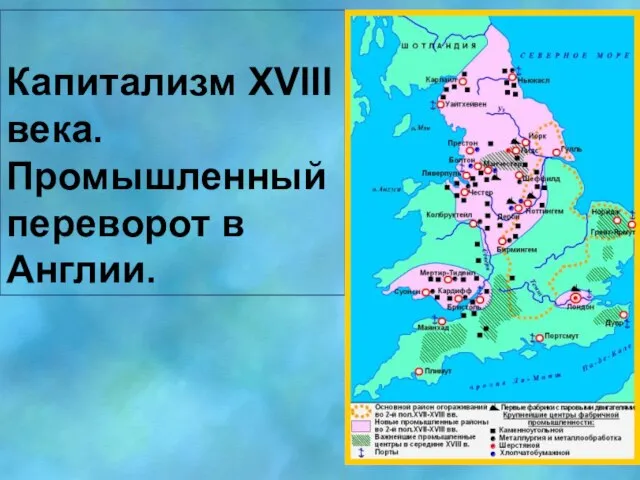 Капитализм XVIII века. Промышленный переворот в Англии
Капитализм XVIII века. Промышленный переворот в Англии Работать с молодёжью: как?
Работать с молодёжью: как?