Содержание
- 2. Эконофизика. Этапы развития 1995 1997 2001 2002 2009 Настоящее время Появление термина для обозначения работ специалистов
- 3. План доклада История науки о финансовых временных рядах Анализ эмпирических данных. Универсальные распределения Фрактальный анализ финансовых
- 4. Финансовые временные ряды. История. Динамический подход. 90-е гг. 19 в. – Формулировка принципов Ч. Доу (Ch.
- 5. Финансовые временные ряды. История. Стохастический подход. L. Bachelier (1900) ПЕРВЫЙ ПОСТУЛАТ. Приращения цены на непересекающихся временных
- 6. Финансовые временные ряды История. Стохастический подход Отказ от постулата независимости Fractional Brownian motion (B. Mandelbrot, 1968)
- 7. Финансовые временные ряды История. Стохастический подход Отказ от постулата нормальности (B. Mandelbrot, 1963) Скейлинговый принцип: на
- 8. Распределение Леви (Levi, 1925) Общий вид устойчивого распределения:
- 9. Распределение Леви
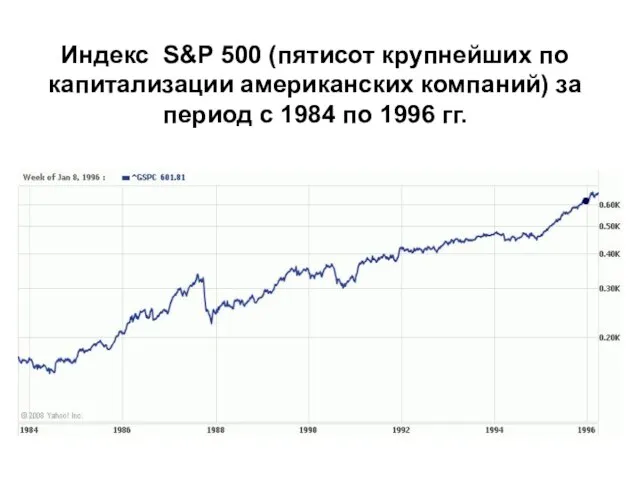
- 10. Индекс S&P 500 (пятисот крупнейших по капитализации американских компаний) за период с 1984 по 1996 гг.
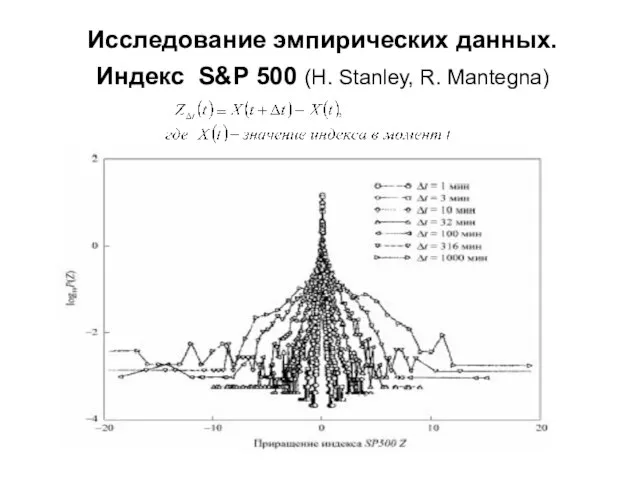
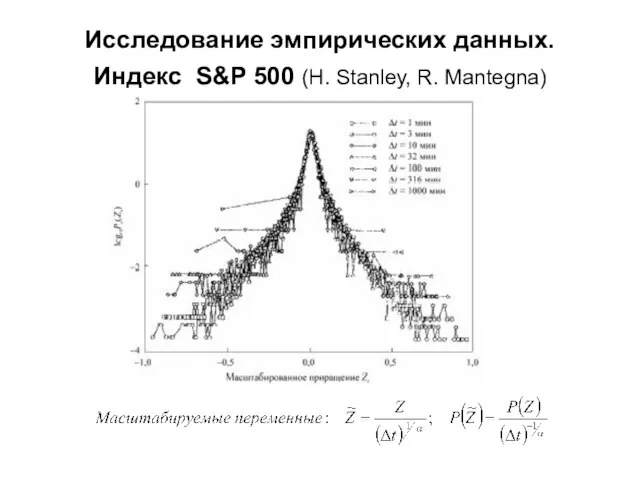
- 11. Исследование эмпирических данных. Индекс S&P 500 (H. Stanley, R. Mantegna)
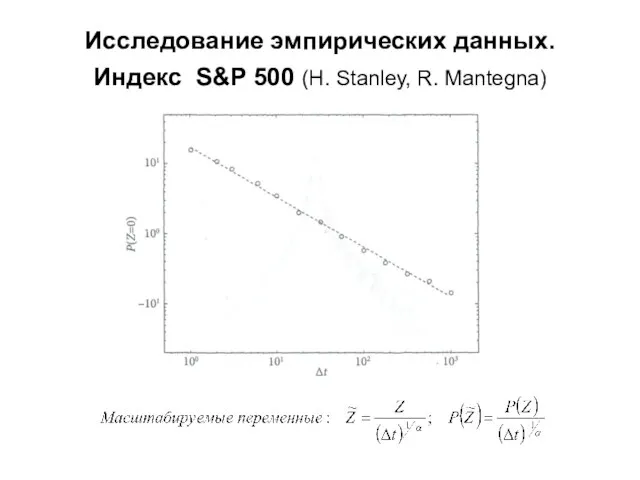
- 12. Исследование эмпирических данных. Индекс S&P 500 (H. Stanley, R. Mantegna)
- 13. Исследование эмпирических данных. Индекс S&P 500 (H. Stanley, R. Mantegna)
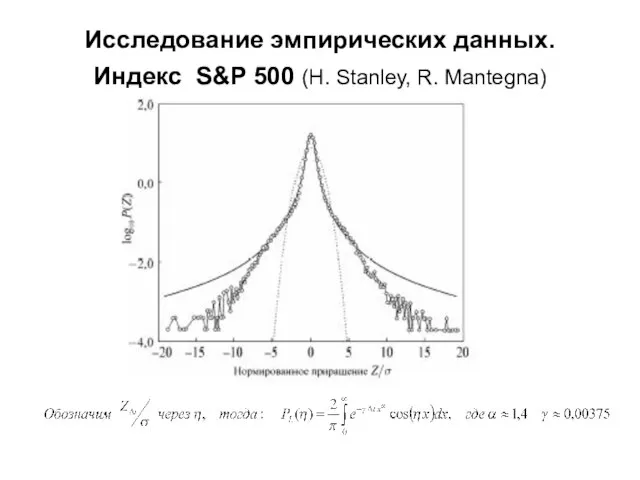
- 14. Исследование эмпирических данных. Индекс S&P 500 (H. Stanley, R. Mantegna)
- 15. Исследование эмпирических данных редких событий (P. Gopikrishnan, V. Plerou, H. Stanley)
- 16. Фракталы Определение размерности (F. Hausdorff, 1919) (для компактного множества в произвольном метрическом пространстве) Мотивация: (D=1,2,3)
- 17. Фракталы Фрактал – это множество, для которого хаусдорфова размерность D строго больше его топологической размерности DT
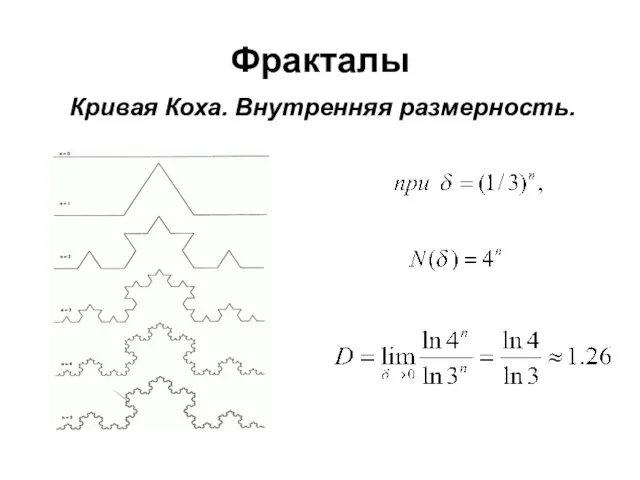
- 18. Фракталы Кривая Коха. Внутренняя размерность.
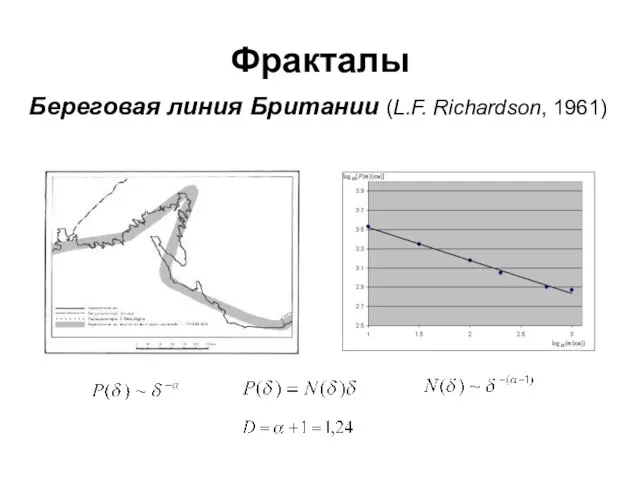
- 19. Фракталы Береговая линия Британии (L.F. Richardson, 1961)
- 20. Отличия природных фракталов от модельных Во-первых, естественные фракталы не бывают строго симметричными. Свойство же самоподобия для
- 21. Фракталы Финансовые временные ряды Движения цен большинства финансовых инструментов внешне похожи, на разных масштабах времени и
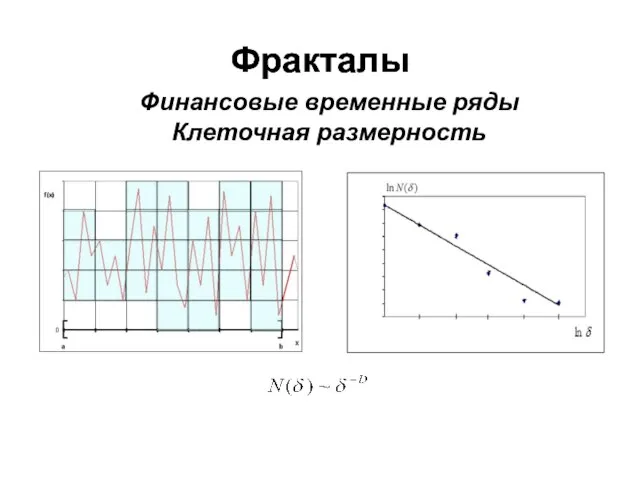
- 22. Фракталы Финансовые временные ряды Клеточная размерность Фракталы
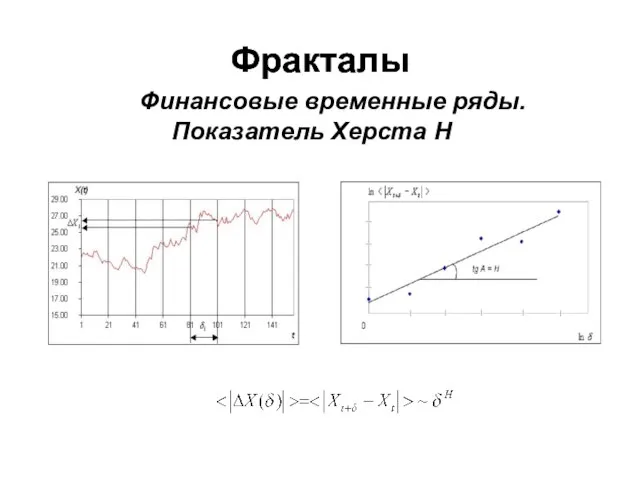
- 23. При H 0,5 – временной ряд находится в состоянии случайного блуждания При H > 0,5 –
- 24. Фракталы Финансовые временные ряды. Показатель Херста H Фракталы
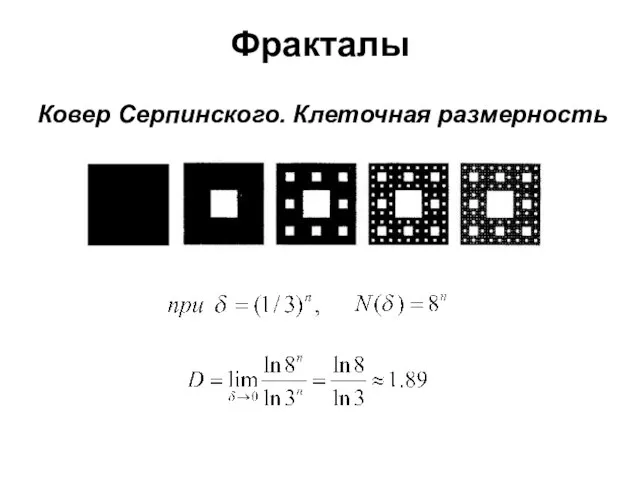
- 25. Фракталы Ковер Серпинского. Клеточная размерность
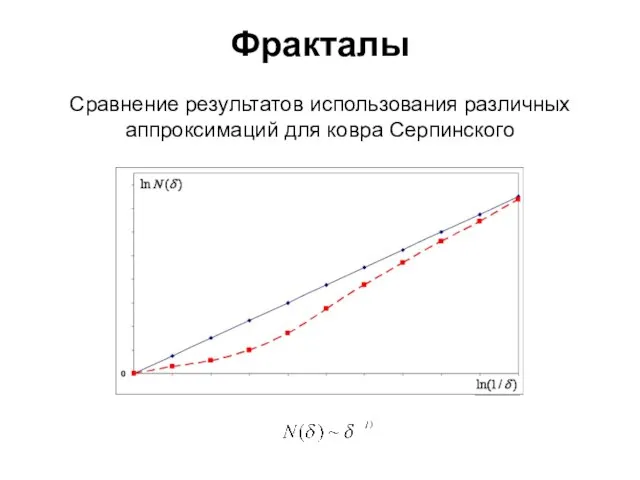
- 26. Фракталы Сравнение результатов использования различных аппроксимаций для ковра Серпинского
- 27. Фракталы Финансовые временные ряды. Асимптотика для площади покрытий
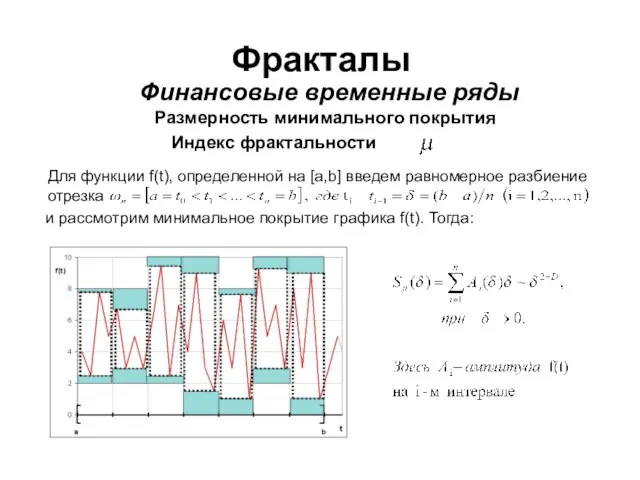
- 28. Фракталы Финансовые временные ряды Размерность минимального покрытия Индекс фрактальности Для функции f(t), определенной на [a,b] введем
- 29. Фракталы Финансовые временные ряды Размерность минимального покрытия Индекс фрактальности Введем обозначение: Поскольку Назовем - индексом фрактальности
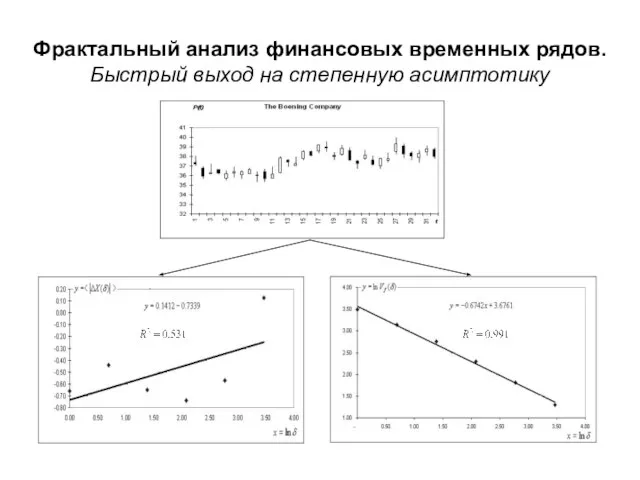
- 30. Фрактальный анализ финансовых временных рядов. Быстрый выход на степенную асимптотику
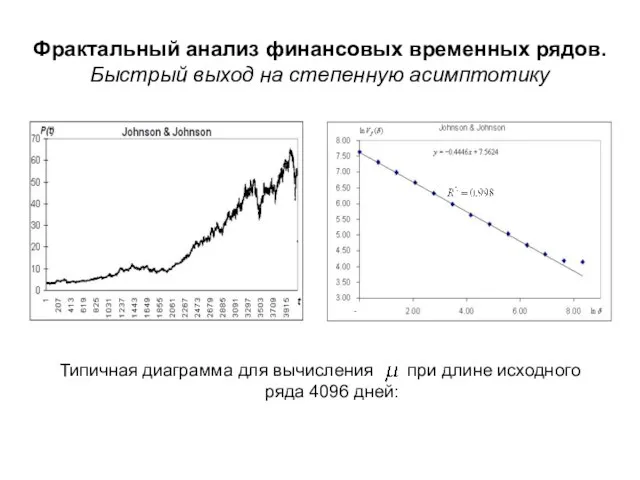
- 31. Фрактальный анализ финансовых временных рядов. Быстрый выход на степенную асимптотику Типичная диаграмма для вычисления при длине
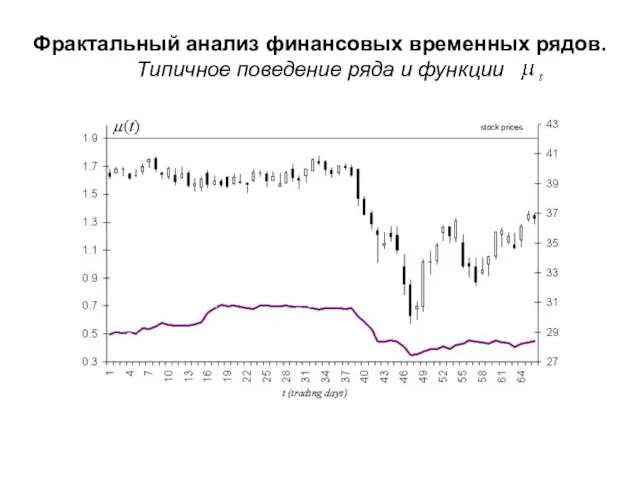
- 32. Фрактальный анализ финансовых временных рядов. Типичное поведение ряда и функции
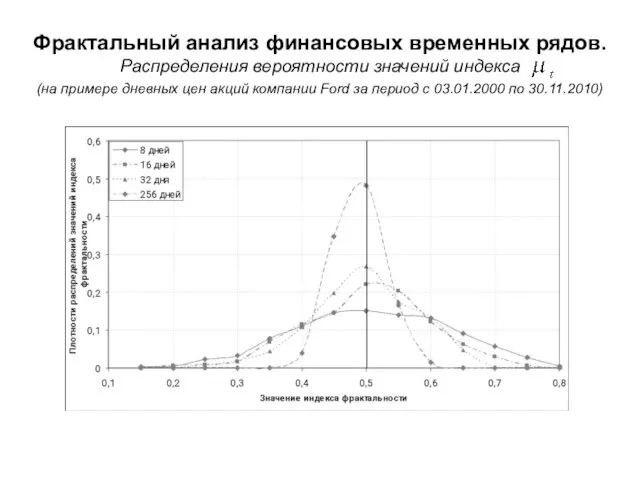
- 33. Фрактальный анализ финансовых временных рядов. Распределения вероятности значений индекса (на примере дневных цен акций компании Ford
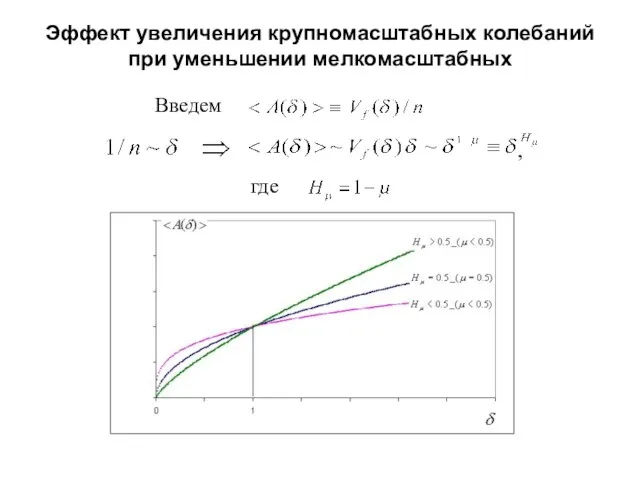
- 34. Эффект увеличения крупномасштабных колебаний при уменьшении мелкомасштабных Введем где ,
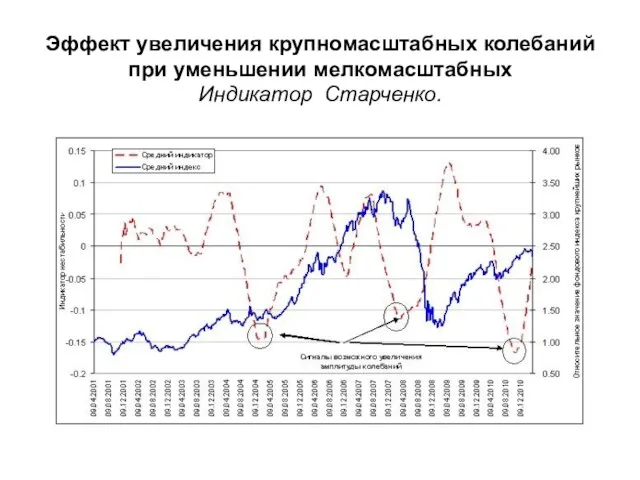
- 35. Эффект увеличения крупномасштабных колебаний при уменьшении мелкомасштабных Индикатор Старченко.
- 36. Модели обвалов на финансовом рынке 1. Инвесторы и спекулянты. Самоорганизованная критичность (P. Back) 2. Модели взаимодействующих
- 37. Модели обвалов на финансовом рынке 2. a) Решетчатые модели. Модель Изинга. Перколяция.
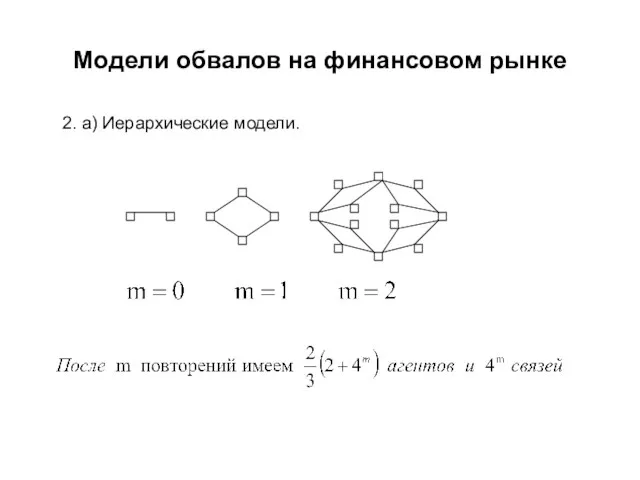
- 38. Модели обвалов на финансовом рынке 2. a) Иерархические модели.
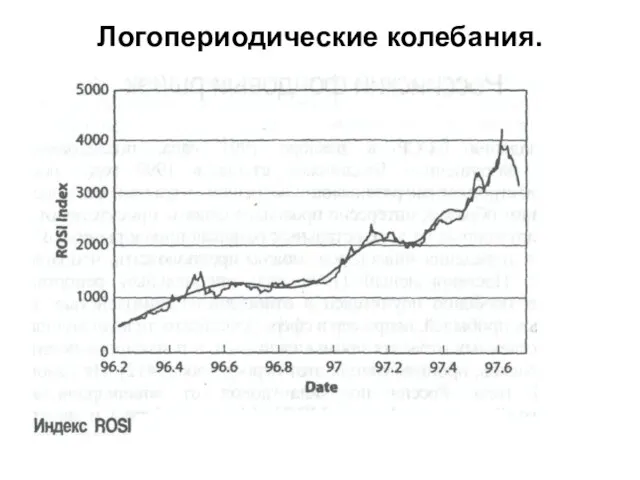
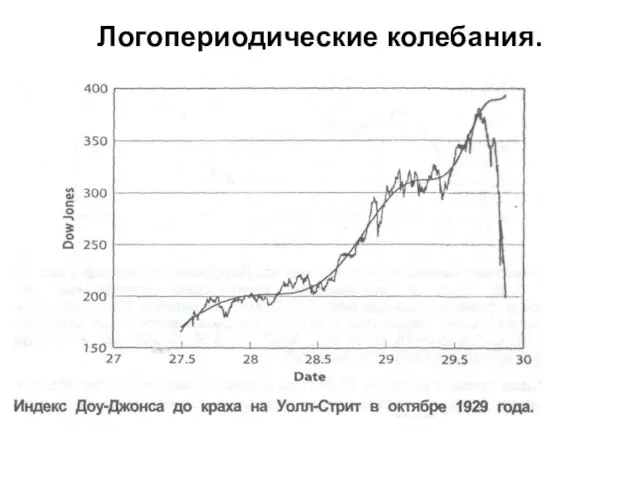
- 39. Модели обвалов на финансовом рынке 2. a) Иерархические модели. Логопериодические колебания.
- 40. Логопериодические колебания.
- 41. Логопериодические колебания.
- 42. Minority Game Модели взаимодействующих агентов K
- 43. Minority Game (Arthur W.B., Challet D., Lux T., Marsili M., Zhang Y-C)
- 44. Minority Game (Arthur W.B., Challet D., Lux T., Marsili M., Zhang Y-C) Некоторые результаты: Существует функция
- 45. Другие разделы экономики: 1. Распределение богатства (V. Yakovenko, A. Dragulescu, М. Романовский) 2. Фирмы.(L. Amaral, S.
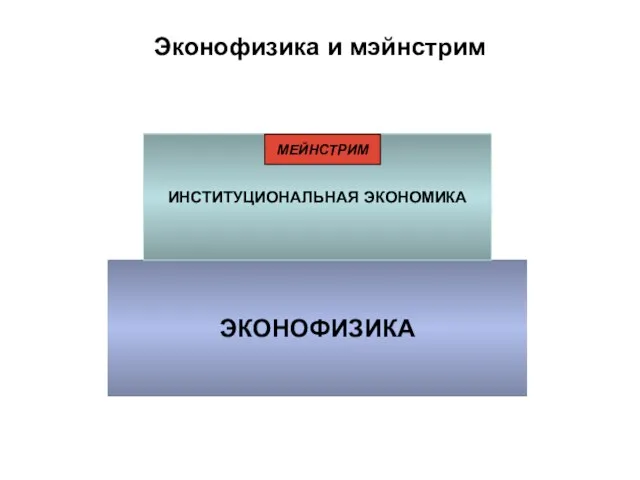
- 46. Эконофизика и мэйнстрим «Лежащее в основе современной экономической теории представление о человеке, который, исходя из рациональной
- 47. Эконофизика и мэйнстрим … Но в Новое Время ситуация изменилась. Бурное развитие международной торговли вывело экономику
- 48. Эконофизика и мэйнстрим ЭКОНОФИЗИКА ИНСТИТУЦИОНАЛЬНАЯ ЭКОНОМИКА МЕЙНСТРИМ
- 49. Литература: 1. Мантенья Р.Н., Стенли Г.Ю. Введение в эконофизику. URSS. М.: 2009 2. Сорнетте Дидье. Как
- 51. Скачать презентацию


























 Современные возможности пробиотической терапии в клинике внутренних болезней
Современные возможности пробиотической терапии в клинике внутренних болезней Территория смыслов
Территория смыслов Карта пробных ароматов: Al Haramain/Aysha (милая)
Карта пробных ароматов: Al Haramain/Aysha (милая) Понятие мониторинга
Понятие мониторинга Прием письменного вычитания в случаях вида 50-24
Прием письменного вычитания в случаях вида 50-24 Акварельные зарисовки
Акварельные зарисовки Русские народные сказки
Русские народные сказки Красная книга растений
Красная книга растений Биография. Шаблон
Биография. Шаблон Дифференциальная диагностика и принципы лечения синдрома Корнелии Де ЛАНГЕ
Дифференциальная диагностика и принципы лечения синдрома Корнелии Де ЛАНГЕ Презентация на тему Телескоп
Презентация на тему Телескоп Презентация Сушильникова Н.И. Экологическая сказка
Презентация Сушильникова Н.И. Экологическая сказка Телеметрическая платформа M2MGate Solution
Телеметрическая платформа M2MGate Solution Китайский клуб МИИТа
Китайский клуб МИИТа Тема выпускной квалификационной работы. Шаблон
Тема выпускной квалификационной работы. Шаблон Морской порт Санкт-Петербург. Отчет по результатам линейного обхода
Морской порт Санкт-Петербург. Отчет по результатам линейного обхода С днем рождения!!!
С днем рождения!!! Муниципальное дошкольное образовательное учреждение «Детский сад № 15» г. Чебоксары
Муниципальное дошкольное образовательное учреждение «Детский сад № 15» г. Чебоксары Презентация на тему Климат Африки
Презентация на тему Климат Африки Коммуникативный практикум
Коммуникативный практикум Государство. Понятие. Теории происхождения
Государство. Понятие. Теории происхождения Жизнь прекрасна
Жизнь прекрасна Измерение расхода. FR — лидер в новейшей высокоточной технологии измерения расхода
Измерение расхода. FR — лидер в новейшей высокоточной технологии измерения расхода Венев
Венев ПУТЕШЕСТВИЕ ПО МАТЕРИКАМ
ПУТЕШЕСТВИЕ ПО МАТЕРИКАМ Экономия водоснабжения
Экономия водоснабжения Рифмоплёт
Рифмоплёт Вареники с картошкой
Вареники с картошкой