Содержание
- 2. Историческая справка Основы формальной логики заложил Аристотель ( 384 -322 гг. до н.э.). Ввел основные формы
- 3. Логика – это наука о формах и способах мышления. Логика изучает мышление как средство познания объективного
- 4. В основе логических схем и устройств ПК лежит специальный математический аппарат, использующий законы логики. Математическая логика
- 5. Основные формы мышления Основными формами мышления являются: ПОНЯТИЯ, ВЫСКАЗЫВАНИЯ, УМОЗАКЛЮЧЕНИЯ. ПОНЯТИЕ- форма мышления, в которой отражаются
- 6. УМОЗАКЛЮЧЕНИЕ – это форма мышления, посредством которой из одного или нескольких истинных суждений, называемых посылками, мы
- 7. Высказывание – повествовательное предложение, в котором что-либо утверждается или отрицается о свойствах реальных объектах или отношениях
- 8. Алгебра высказываний Простым высказываниям ставятся в соответствие логические переменные. Пример: А = «2 * 2 =
- 9. Логическое отрицание (инверсия) Присоединение частицы «не» к высказыванию. Делает истинное высказывание ложным, а ложное – истинным.
- 10. Логическое умножение (конъюнкция) Объединение двух (или нескольких) высказываний в одно с помощью союза «и». Обозначение: А
- 11. Логическое сложение (дизъюнкция) Объединение двух (или нескольких) высказываний в одно с помощью союза «или». Обозначение: А
- 12. Импликация (логическое следование) Соответствующие выражения языка: Если A, то B A достаточно для B B следует
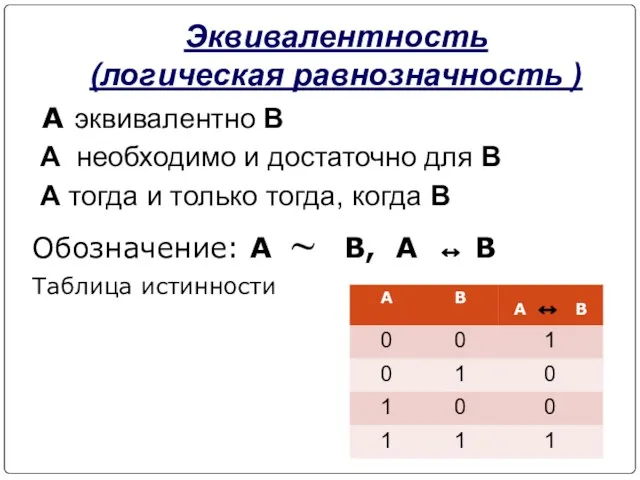
- 13. Эквивалентность (логическая равнозначность ) A эквивалентно B A необходимо и достаточно для B A тогда и
- 14. Таблицы истинности Для каждого составного высказывания (логического выражения) можно построить таблицу истинности, которая определяет истинность или
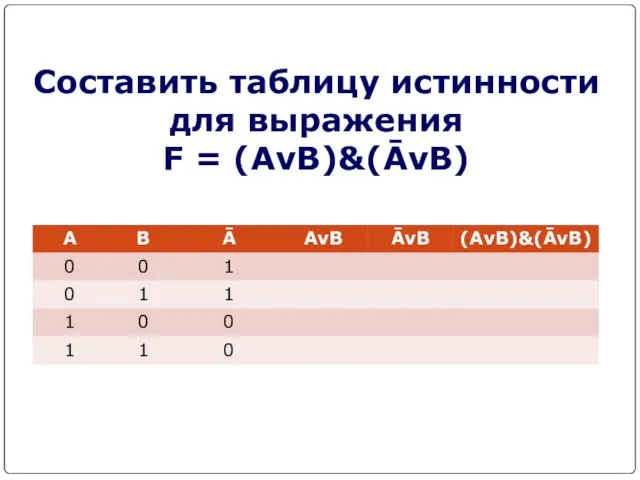
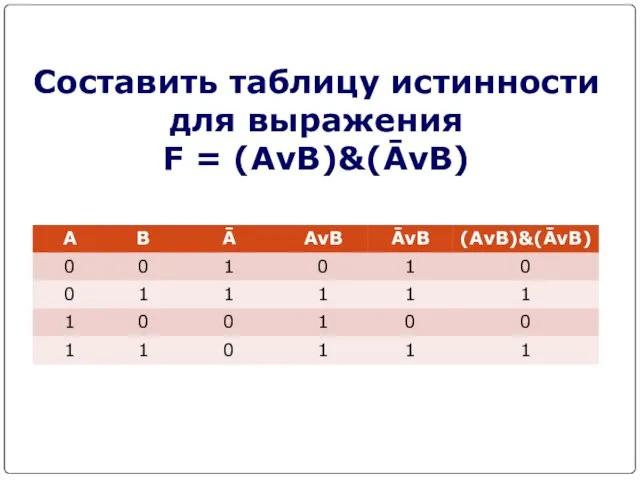
- 15. Составить таблицу истинности для выражения F = (AvB)&(ĀvB)
- 16. F = (AvB)&(ĀvB) Количество входных переменных в заданном выражении равно двум (A,B). Значит, количество входных наборов,
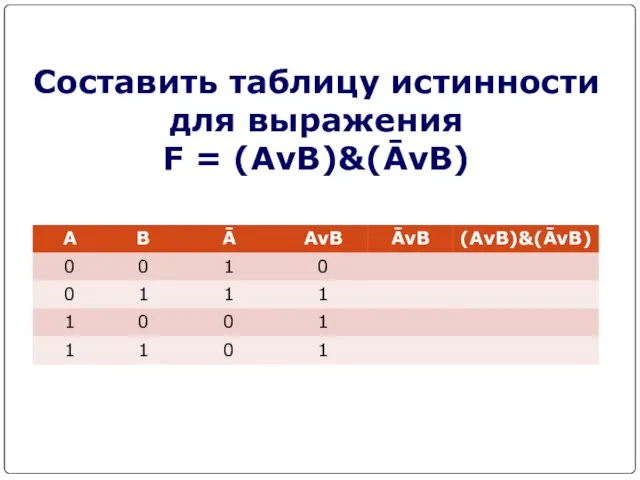
- 17. Составить таблицу истинности для выражения F = (AvB)&(ĀvB)
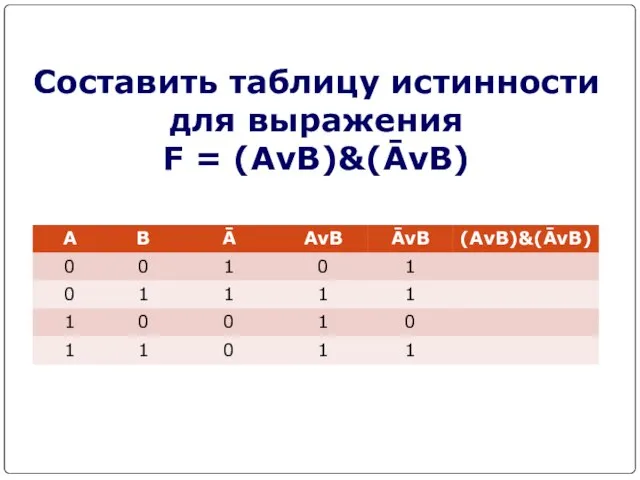
- 18. Составить таблицу истинности для выражения F = (AvB)&(ĀvB)
- 19. Составить таблицу истинности для выражения F = (AvB)&(ĀvB)
- 20. Составить таблицу истинности для выражения F = (AvB)&(ĀvB)
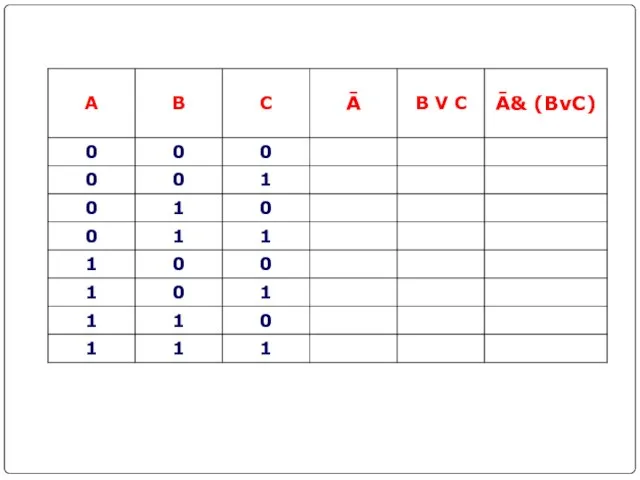
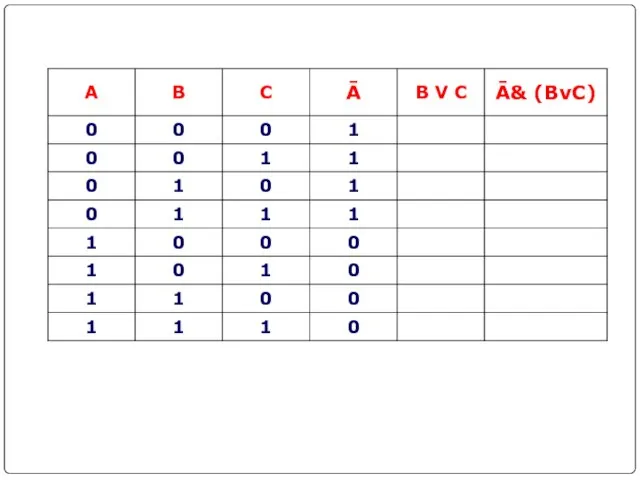
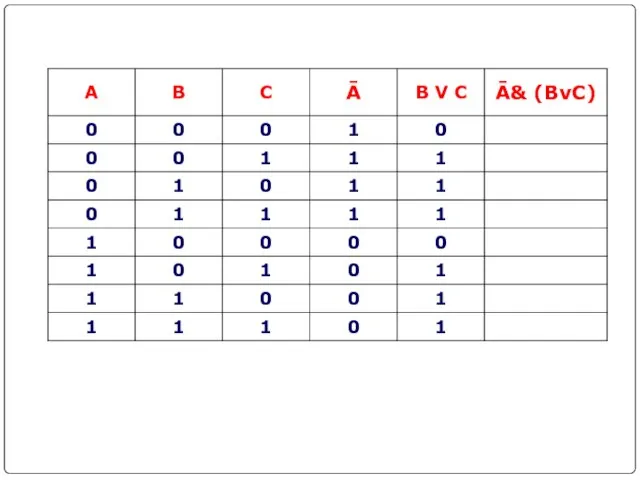
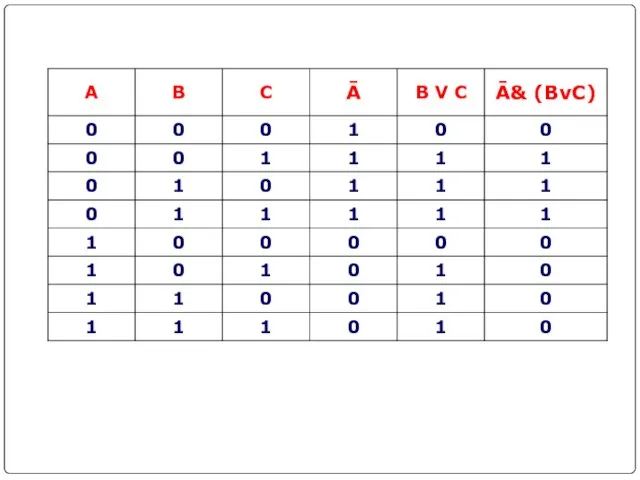
- 21. Составить таблицу истинности для логической функции: 1. Количество входных переменных в заданном выражении равно трем (A,B,C).
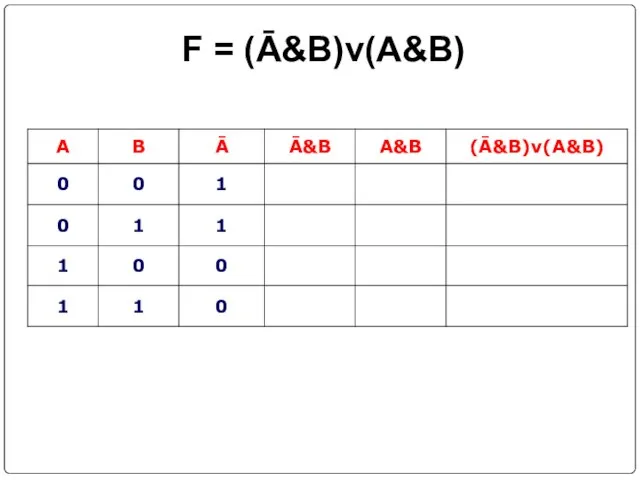
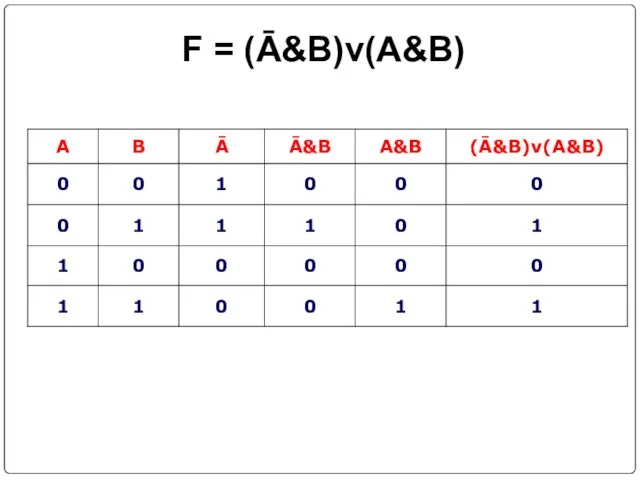
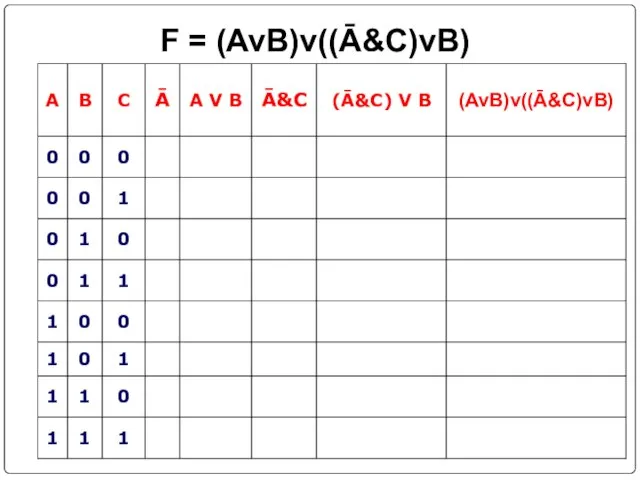
- 26. Составить таблицы истинности F = (Ā&B)v(A&B) F = (AvB)v((Ā&C)vB) F= (A&C ) → (( AvB)↔C)
- 27. F = (Ā&B)v(A&B)
- 28. F = (Ā&B)v(A&B)
- 29. F = (AvB)v((Ā&C)vB)
- 31. Скачать презентацию
















 Неметаллы
Неметаллы Конструирование шкатулки из бросового материала
Конструирование шкатулки из бросового материала Кафедра ТИССУ
Кафедра ТИССУ Проект Зелёное кольцо
Проект Зелёное кольцо Урок литературного чтения в 1 классе
Урок литературного чтения в 1 классе Горные и маркшейдерские работы применительно к условиям разработки Лебединского месторождения
Горные и маркшейдерские работы применительно к условиям разработки Лебединского месторождения Химическая и нефтехимическая промышленность в России: роль государства в преодолении кризиса и дальнейшем развитии отрасли
Химическая и нефтехимическая промышленность в России: роль государства в преодолении кризиса и дальнейшем развитии отрасли Оптимизация процесса настройки рабочего места для работы в Единой информационной системе в сфере закупок
Оптимизация процесса настройки рабочего места для работы в Единой информационной системе в сфере закупок Презентация на тему Применение фотоэффекта
Презентация на тему Применение фотоэффекта ПРОГРАММЫ ПОДГОТОВКИ ЛЮБИТЕЛЬСКИХ КОМАНД
ПРОГРАММЫ ПОДГОТОВКИ ЛЮБИТЕЛЬСКИХ КОМАНД Роль отца в воспитании ребенка
Роль отца в воспитании ребенка Волевые качества
Волевые качества Урок-открытие
Урок-открытие Институциональные репозитории: создание и управление
Институциональные репозитории: создание и управление Паровые машины
Паровые машины Уимблдон
Уимблдон Современные модели образовательного процесса соответствии с ФГТ
Современные модели образовательного процесса соответствии с ФГТ Реклама в торговом комплексе «Фиолент»
Реклама в торговом комплексе «Фиолент» VXlkbvvDUSz19pGVCwhRfQ
VXlkbvvDUSz19pGVCwhRfQ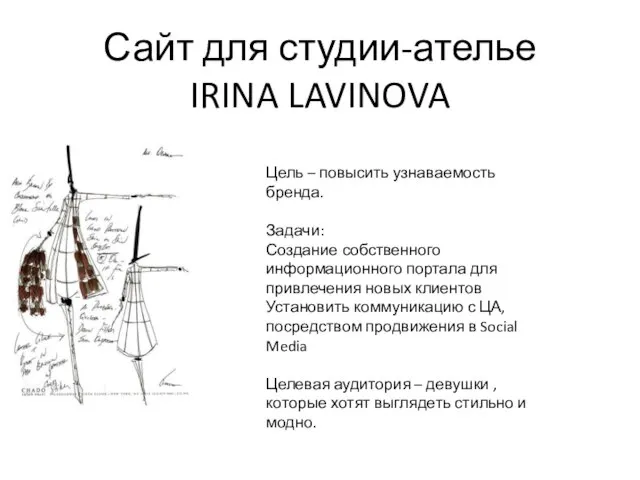 Сайт для студии-ателье IRINA LAVINOVA
Сайт для студии-ателье IRINA LAVINOVA Kuv_2022_MS_13_Recons_авг (1)
Kuv_2022_MS_13_Recons_авг (1) Презентацию составила учитель математики БОУ СОШ26 п.Украинский Динского района Краснодарского края Краснощекова Л.Г.
Презентацию составила учитель математики БОУ СОШ26 п.Украинский Динского района Краснодарского края Краснощекова Л.Г. Живопись. Гармония по общему цветовому тону (тема 18)
Живопись. Гармония по общему цветовому тону (тема 18) www.ratsp.ru
www.ratsp.ru Последовательное соединение проводников
Последовательное соединение проводников Равнины и горы России
Равнины и горы России Фестиваль Бархатный сезон. Ялта
Фестиваль Бархатный сезон. Ялта Курс лекций по дисциплине Экология
Курс лекций по дисциплине Экология