ОСНОВЫ МАТЕМАТИЧЕСКОЙ ОБРАБОТКИ ИНФОРМАЦИИ

Определения
Основа - исходные, главные положения какой-л. отрасли знаний или направления научной деятельности, теории и т.п.

Определения
Вся продуктивная деятельность человека так или иначе связана с обработкой информации. Процесс развития общества неотделим от становления все более полных и эффективных методов обработки информации. Каждая область науки и в большой степени различные отрасли деятельности (образование, экономика, экология, добывающие отрасли, транспорт, связь, медицинская диагностика, управление и т.д.) представляют собой совокупность идей и методов, предназначенных для целенаправленной и эффективной обработки той информации, за которую ответственна данная область.

Определения
Основу методов обработки информации составляют вычислительная математика, теория информации и математическая статистика.

Определения
Обработка информации состоит в получении одних «информационных объектов» из других «информационных объектов» путем выполнения некоторых алгоритмов и является одной из основных операций, осуществляемых над информацией.
Можно выделить числовую и нечисловую обработку информации.

Определения
Математическая обработка информации сводится, по большей части, к обработке данных с помощью различных методов.
Метод - способ действия в процессе познания чего-л.; последовательность действий при теоретическом исследовании чего-л.

Основные методы
1. Компьютерные методы
2. Метод построения математических моделей.
3. Статистические методы.
4. Графические методы.

1. Компьютерные методы
Компьютер значительно расширяет возможности в обработке математических данных.

1. Компьютерные методы
Использование табличных процессоров (Excel и др.), специализированных математических пакетов (MathCad, Maple и др. ), статистических пакетов http://denisvolkov.com/wp-content/uploads/2011/03/KMOD-0.pdf позволяет решать математические задачи различного уровня сложности, тем самым позволяя осуществить математическую обработку информации.

Примеры задач:
работа с матрицами и определителями;
работа с системами линейных уравнений и неравенств;
построение и исследование графиков функций;
построение диаграмм, гистограмм;
математическая обработка экспериментальных данных;
др.

Решение линейной системы методом Гаусса в MathCad
Методы решения систем линейных алгебраических уравнений можно разделить на точные и приближенные.
Метод решения задачи относят к классу точных, если в предположении отсутствия округления с его помощью можно найти решение в результате конечного числа арифметических и логических операций.

Решение линейной системы методом Гаусса в MathCad
Метод Гаусса – точный метод решения невырожденной системы линейных алгебраических уравнений.
В MathCad прямой и обратный ходы выполняет функция rreff(A).

Моделирование
Основной путь исследования системы – это построение модели. Моделирование – процесс, посредством которого исследователь стремится понять определенные аспекты реальной жизни. Модель не является точной копией реальности, а представляет собой упрощенный ее вариант, согласованный с задачами исследователя. Один и тот же объект в зависимости от целей исследования может иметь разные модели.

Моделирование
В дальнейшем под моделированием мы будем понимать теоретические модели реальности, а не процесс изготовления моделей каких-либо предметов, например самолетов.
Моделирование как метод исследования имеет альтернативу. Это – словесный, или «вербальный», анализ, оперирующий произвольными категориями с расплывчатыми результатами, которые трудно оценить. Нисколько не умаляя достоинств этого метода исследования, уместно указать на часто встречающийся недостаток «вербального» анализа: «Не пользующаяся математическими сим­волами человеческая логика зачастую запутывается в словесных определениях и делает вследствие этого ошибочные выводы – и вскрыть эту ошибку за музыкою слов иногда стоит огромного труда и бесконечных, часто бесплодных, споров» (В.И. Арнольд «Жесткие и мягкие модели»).

Моделирование
Моделирование – это прежде всего умение выделить главное. Модели должны быть по возможности простыми, од­нако они должны включать все самые важные части исследуе­мой системы (оригинала), самые важные функции и самые важ­ные связи, внутрисистемные и внешние. Но таких элементов, выбранных для последующего детального исследования, долж­но быть ограниченное, небольшое количество, иначе будет трудно вести анализ.

Моделирование
Для того чтобы найти главные части и связи системы, следует сосредоточить внимание на трех важных моментах:
Определить главную цель системы, ответив на вопросы о том, зачем существует система и какие главные функции она выполняет.
Понять работу системы и определить главные части (подсистемы), участвующие в выполнении главной функции.
Установить важные связи между этими частями.
При этом связи и части системы будут действительно важными, если после их исключения из нее система «рассыпается». И наоборот, если мы исключили какую-то часть или связь и ничего не изменилось, то это не главная часть или, соответствен­но, не важная связь.

Советы
Научиться моделированию, ограничившись только формаль­ным усвоением каких-то правил, конечно, невозможно. Но все же есть со­веты, к которым стоит прислушаться. Например, к советам ака­демика Ю.И. Неймарка. Они достаточно общие и не могут служить непосредственным указанием к действию, но дают разумные подсказки, что и как следует делать:
Чем проще модель, тем меньше возможность ошибочных выводов.
Модель должна быть простой, но не проще, чем это воз­можно.
Пренебрегать можно чем угодно, нужно только знать, как это повлияет на решение.
Модель должна быть грубой: малые поправки не должны кардинально менять ее поведение.
Модель и расчет не должны быть точнее исходных данных.

Основные принципы построения матема­тической модели
Необходимо соизмерять точность и подробность модели, во-первых, с точностью тех исходных данных, которыми располагает исследователь, и, во-вторых, с теми результатами, которые требуется получить.
Математическая модель должна отражать существенные черты иссле­дуемого явления и при этом не должна его сильно упрощать.
Математическая модель не может быть полностью адекватна реально­му явлению, поэтому для его исследования лучше использовать не­сколько моделей, для построения которых применены разные матема­тические методы. Если при этом получаются сходные результаты, то исследование заканчивается. Если результаты сильно различаются, то следует пересмотреть постановку задачи.
Любая сложная система всегда подвергается малым внешним и внут­ренним воздействиям, следовательно, математическая модель должна быть устойчивой, т.е. сохранять свои свойства и структуру при этих воздействиях.

Метод построения математических моделей
Приближённое описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики. М. м. — мощный метод познания внешнего мира, а также прогнозирования и управления. Анализ М. м. позволяет проникнуть в сущность изучаемых явлений.

Этапы
Процесс математического моделирования, то есть изучения явления с помощью М. м., можно подразделить на 4 этапа.

Первый этап
формулирование законов, связывающих основные объекты модели. Этот этап требует широкого знания фактов, относящихся к изучаемым явлениям, и глубокого проникновения в их взаимосвязи. Эта стадия завершается записью в математических терминах сформулированных качеств, представлений о связях между объектами модели.

Второй этап
исследование математических задач, к которым приводят М. м. Основным вопросом здесь является решение прямой задачи, то есть получение в результате анализа модели выходных данных (теоретических следствий) для дальнейшего их сопоставления с результатами наблюдений изучаемых явлений. На этом этапе важную роль приобретают математический аппарат, необходимый для анализа М. м., и вычислительная техника — мощное средство для получения количеств, выходной информации как результата решения сложных математических задач. Часто математические задачи, возникающие на основе М. м. различных явлений, бывают одинаковыми (например, основная задача линейного программирования (См. Линейное программирование) отражает ситуации различной природы). Это даёт основание рассматривать такие типичные математические задачи как самостоятельный объект, абстрагируясь от изучаемых явлений.

Третий этап
выяснение того, удовлетворяет ли принятая гипотетическая модель критерию практики, то есть выяснение вопроса о том, согласуются ли результаты наблюдений с теоретическими следствиями модели в пределах точности наблюдений. Если модель была вполне определена — все параметры её были заданы, — то определение уклонений теоретических следствий от наблюдений даёт решения прямой задачи с последующей оценкой уклонений. Если уклонения выходят за пределы точности наблюдений, то модель не может быть принята. Часто при построении модели некоторые её характеристики остаются не определёнными. Задачи, в которых определяются характеристики модели (параметрические, функциональные) таким образом, чтобы выходная информация была сопоставима в пределах точности наблюдений с результатами наблюдений изучаемых явлений, называются обратными задачами. Если М. м. такова, что ни при каком выборе характеристик этим условиям нельзя удовлетворить, то модель непригодна для исследования рассматриваемых явлений. Применение критерия практики к оценке М. м. позволяет делать вывод о правильности положений, лежащих в основе подлежащей изучению (гипотетической) модели. Этот метод является единственным методом изучения недоступных нам непосредственно явлений макро- и микромира.

Четвертый этап
последующий анализ модели в связи с накоплением данных об изучаемых явлениях и модернизация модели. В процессе развития науки и техники данные об изучаемых явлениях всё более и более уточняются и наступает момент, когда выводы, получаемые на основании существующей М. м., не соответствуют нашим знаниям о явлении. Т. о., возникает необходимость построения новой, более совершенной М. м.

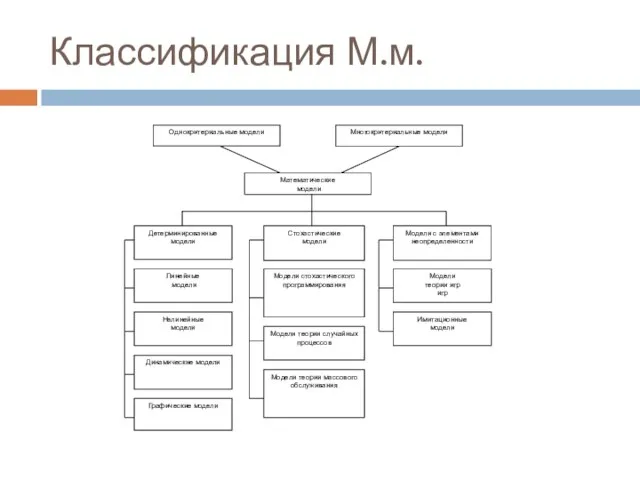
Классификация М.м.

Примеры
Модель Солнечной системы. Наблюдения звёздного неба начались в глубокой древности. Первичный анализ этих наблюдений позволил выделить планеты из всего многообразия небесных светил. Таким образом, первым шагом было выделение объектов изучения. Вторым шагом явилось определение закономерностей их движений. (Вообще определения объектов и их взаимосвязей являются исходными положениями — «аксиомами» — гипотетической модели.) Модели Солнечной системы в процессе своего развития прошли через ряд последовательных усовершенствований. Первой была модель Птолемея (2 век н. э.), исходившая из положения, что планеты и Солнце совершают движения вокруг Земли (геоцентрическая модель), и описывавшая эти движения с помощью правил (формул), многократно усложнявшихся по накоплении наблюдений.
Другие примеры http://mat.1september.ru/2003/14/no14_1.htm

Примеры
Экономико-математические модели: функции полезности; кривые безразличия; функции спроса; уравнение Слуцкого; Кривые «доход –потребление»; кривые «цены – потребление»; коэффициент эластичности; материальные балансы; функции выпуска продукции; производственные функции затрат ресурсов; модели поведения фирмы в условиях совершенной и несовершенной конкуренции; модели общего экономического равновесия; модель Эрроу – Гурвица; статистическая и динамическая модели межотраслевого баланса; общие модели развития экономики

Вывод
Метод математического моделирования, сводящий исследование явлений внешнего мира к математическим задачам, занимает ведущее место среди других методов исследования, особенно в связи с появлением ЭВМ. Он позволяет проектировать новые технические средства, работающие в оптимальных режимах, для решения сложных задач науки и техники; проектировать новые явления. М. м. проявили себя как важное средство управления. Они применяются в самых различных областях знания, стали необходимым аппаратом в области экономического планирования и являются важным элементом автоматизированных систем управления.

Графические методы
К графическим методам обработки информации можно отнести:
Графики
Диаграммы
Графы

Графики
Современную науку невозможно представить без применения графиков. Они стали средством научного анализа и обобщения. Такие свойства графиков, как выразительность, доходчивость, лаконичность, универсальность, смысловая однозначность, интернациональность, легкость кодирования, а также обозримость графических изображений сделали их незаменимыми в исследовательской и практической работе и в сопоставлениях как в технических вопросах, так и в вопросах социал

Графики
Графики нашли широкое применение для передачи различного рода информации в разных сферах жизни, что обусловило разнообразие их видов. Это привело к многозначности понятия графика, отсутствию в настоящее время четких критериев терминологии и классификации. Одним из видов графиков является график наглядного изображения количественной зависимости различных массовых явлений, процессов и т. д. Названия этих графиков различны: статистические графики, диаграммы, статистические диаграммы.
Другими видами графиков являются номограммы - расчетные графики, целью которых является вычисление результатов при всевозможных комбинациях частных значений переменных, от которых этот результат зависит. Номограммы являются удобным вычислительным инструментом. К другим видам графиков относятся оргасхемы - структурные схемы организации предприятия; графики движения транспорта; графики-расписания работы предприятий, контрольно-плановые графики организации производства и т. д.

Особенности графического языка
Двухмерность записи: при передаче информации графическим языком используется два измерения - линейная последовательность размещения знаков (строка или ряд строк) и их взаимосвязь на плоскости.
Непрерывность выражения, проявляющаяся в том, что информация, передаваемая с помощью графического языка, представляется посредством системы взаимосвязанных знаков, а не отдельных линейно расположенных дискретных знаков. Этим язык графиков существенным образом отличается от других искусственных языков, например, математического, для которого характерна дискретность знаков и линейная последовательность их расположения.

Особенности графического языка
Обособленность изложения. Информация, передаваемая графическим языком, обычно обособляется от непосредственно связанной с ней по содержанию информации, представленной в словесной или письменно - текстовой форме. Обособленность изложения графического языка непосредственно вытекает из его природы, его способности адекватно передавать количественные и отвлеченные качественные характеристики изучаемых явлений и выявлять из исходной информации новые свойства и особенности, находящиеся в ней в скрытом состоянии.

Метричность и наглядность. Метричность, т.е. использование в графиках масштабных шкал и условных обозначений, позволяет определить отдельные показатели, уровни и размеры изучаемых явлений. Представление информации в виде графика более наглядно и доступно, чем табличное, оно позволяет лучше осмыслить результаты наблюдения, правильно их истолковать, получить новое знание о предмете исследования, обобщая исходную информацию.
Особенности графического языка

Диаграмма
Диаграмма (от греч. - чертеж, фигура, рисунок) представляет собой чертеж, на котором совокупности, характеризуемые определенными показателями, с целью их обобщения и анализа описываются с помощью условных геометрических образов или знаков, являющихся графическим языком.

Диаграммы сравнения
Основное назначение диаграмм сравнения заключается в графическом сопоставлении показателей, что способствует более глубокому и наглядному анализу изучаемых данных.
Диаграммы сравнения по форме графического образа разнообразны: столбиковые диаграммы, которые имеют разновидности - ленточные (полосовые), направленные, диаграммы числовых отклонений; в виде правильных геометрических фигур; фигур - знаков; знаков Варзара.

Столбиковые диаграммы
Среди диаграмм сравнения наиболее распространенными являются столбиковые диаграммы, принцип построения котоҏыҳ состоит в изображении показателей в виде поставленных по вертикали прямоугольников - столбиков. Каждый столбик изображает величину отдельного уровня исследуемого ряда. Итак, сравнение показателей возможно потому, что все они выражены в одной единице измерения.

Ленточные или полосовые диаграммы
Разновидности столбиковых диаграмм составляют так называемые ленточные или полосовые диаграммы. Их отличие от столбиковых диаграмм состоит в том, что масштабная шкала расположена по горизонтали вверху или внизу, и она определяет величину полос по длине. Область применения столбиковых и полосовых диаграмм одинакова, идентичны также правила их построения. Одномерность изображаемых показателей и их одномасштабность для различных столбиков и полос требуют выполнения единственного положения: соблюдения соразмерности (столбиков - по высоте, полос - по длине) и пропорциональности изображаемым величинам. Для выполнения этого требования необходимо, во-первых, чтобы шкала, по которой устанавливается размер столбика (полосы), начиналась с нуля; во-вторых, эта шкала должна быть непрерывной, т.е. охватывать все числа данного ряда. Разрыв шкалы и соответственно столбиков (полос) не допускается. Невыполнение указанных правил приводит к искаженному графическому представлению анализируемого материала.

Направленные диаграммы
Разновидностью столбиковых (ленточных) диаграмм являются направленные диаграммы. Они отличаются от них двусторонним расположением столбиков или полос и имеют начало отсчета по масштабу в середине. Обычно такие диаграммы применяются для изображения величин противоположного качественного значения. Сравнение между собой столбиков (полос), направленных в разные стороны, менее эффективно, чем расположенных рядом в одном направлении. Несмотря на это, анализ направленных диаграмм позволяет делать достаточно содержательные выводы, так как особое расположение придает графику яркость изображения

Диаграммы числовых отклонений
К группе двусторонних относятся диаграммы числовых отклонений. В них полосы направлены в обе стороны от вертикальной нулевой линии: вправо - для прироста; влево - для уменьшения. С помощью таких диаграмм удобно изображать отклонения от плана или некоторого уровня, принятого за базу сравнения. Важным достоинством рассматриваемых диаграмм является возможность видеть размах изменения изучаемого статистического признака, что само по себе имеет большое значение для экономического анализа.

Диаграммы в виде правильных геометрических фигур
Для простого сравнения независимых друг от друга показателей могут также использоваться диаграммы, принцип построения котоҏыҳ состоит в том, что сравниваемые величины изображаются в виде правильных геометрических фигур, которые строятся так, чтобы площади их относились между собой как количества, изображаемые этими фигурами. Иными словами, эти диаграммы выражают величину изображаемого явления размером своей площади.
Для получения диаграмм рассматриваемого типа используют разнообразные геометрические фигуры - квадрат, круг, реже - прямоугольник. Известно, что площадь квадрата равна квадрату его стороны, а площадь круга пропорциональна квадрату его радиуса. В связи с этим для построения диаграмм необходимо сначала из сравниваемых величин извлечь квадратный корень.

Диаграммы в виде графического изображения одной геометрической фигуры в другой
К рассматриваемому виду диаграмм относится графическое изображение, полученное путем построения одной в другой различных геометрических фигур (квадратов, кругов, прямоугольников и др.) с различной заштриховкой или закраской. При этом в случае построения диаграмм в виде кругов один в другом сравниваются не диаметры окружностей, а угловые размеры секторов.Такие диаграммы позволяют сравнивать между собой ряд исследуемых величин.

Точечные диаграммы
Широко распространенными диаграммами сравнения являются точечные диаграммы, принцип построения котоҏыҳ состоит в изображении показателей в виде поставленных на плоскости точек. Каждая точка изображает величину отдельного уровня исследуемого ряда.
При построении точечных диаграмм необходимо начертить систему прямоугольных координат, в которой располагаются точки. На горизонтальной оси располагается равномерная шкала одной из сравниваемых величин, на вертикальной - шкала другой величины (чаще всего удельный показатель). Точечная диаграмма является наглядной и выразительной лишь при небольшом числе частей совокупности, в противном случае ее применение малоэффективно.

Структурные диаграммы
Основное назначение структурных диаграмм заключается в графическом представлении состава анализируемых совокупностей, характеризующихся как соотношение различных частей каждой из совокупностей. Состав анализируемой совокупности графически может быть представлен с помощью как абсолютных, так и относительных показателей. В первом случае не только размеры отдельных частей, но и размер графика в целом определяются анализируемыми величинами и изменяются в соответствии с изменениями последних. Во втором - размер всего графика не меняется (так как сумма всех частей любой совокупности составляет 100%), а меняются только размеры отдельных его частей. Графическое изображение состава совокупности по абсолютным и относительным показателям способствует проведению более глубокого анализа и позволяет проводить сопоставления и сравнения различных показателей и явлений. В качестве графического образа для изображения структуры совокупностей применяются прямоугольники - для построения столбиковых и полосовых диаграмм, и окружности - для построения секторных диаграмм.