Содержание
- 2. Результаты и успехи Республики Беларусь на международном уровне – 2010‑2018 ITYM – Международные турниры юных математиков
- 3. Успехи на МТЮМ
- 4. Результаты и успехи на международном уровне – 2010‑2019 ICYS – Международные конференции юных ученых (постоянно участвуют
- 5. Успехи на IСYS - 2019 В том числе, участник из Витебска: Нефёдов Илья Игоревич (8 класс
- 6. Деятельность исследовательского характера учащихся РАЗВИВАЕТ! 1. ГЛОБАЛЬНО: умение проводить исследовательскую (творческую, изобретательскую, аналитическую, поисковую) работу; 2.
- 7. Деятельность исследовательского характера учащихся РАЗВИВАЕТ! 7. умение оценить дискуссию других «спорящих», смело высказать свою позицию и
- 8. в возрастном аспекте (самом простом): условное деление – младшая школа (1 – 4 класс и «дошкольники»),
- 9. в уровнях исследовательской работы (уровни исследовательской задачи – уровень сложности) Исследовать (с точки зрения науки) –
- 10. Учебно-исследовательская задача – это задача, несущая в своей постановке элементы и необходимость исследования (т.е. получение знания),
- 11. Исследовательская задача – это действительно задача для исследования, т.е. результатом ее решения будет новое знание: ни
- 12. Научно-исследовательская задача Но в отличие от научно-исследовательской задачи, результатом решения которой является новое научное знание, знание,
- 13. Четкой грани между уровнями исследовательской работы нет, Примеры: Магический квадрат: 2) Теорема Ферма: уравнение xn +
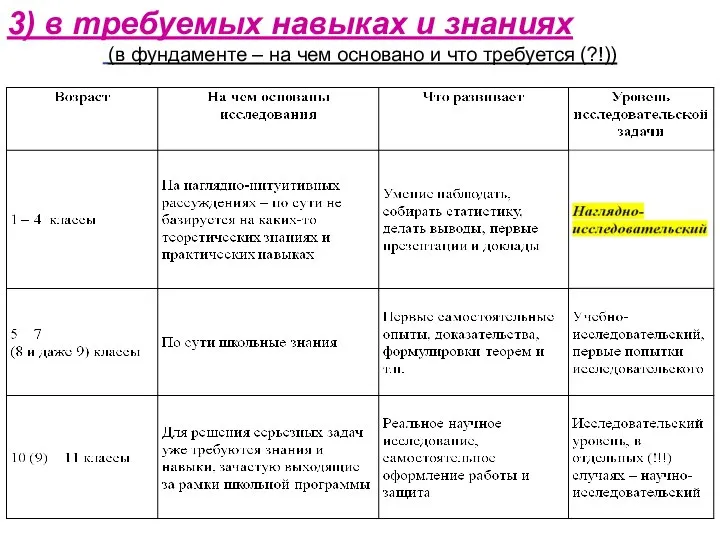
- 14. 3) в требуемых навыках и знаниях (в фундаменте – на чем основано и что требуется (?!))
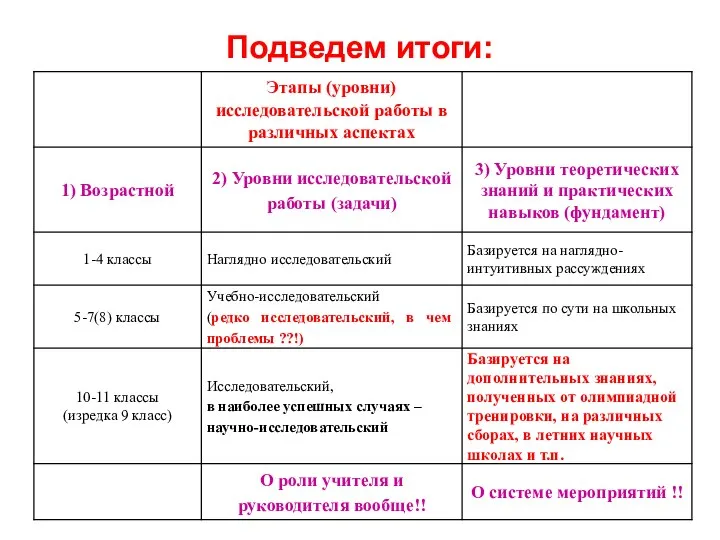
- 15. Подведем итоги:
- 16. СИСТЕМА мероприятий От научно-популярных конкурсов («Мы – наследники Пифагора», математические и другие брейн-ринги, КВНы, Кенгуру, и
- 17. Открытый гимназический турнир юных математиков «Математический Олимп» Место проведения: Государственное учреждение образования «Гимназия №51 г. Гомеля»
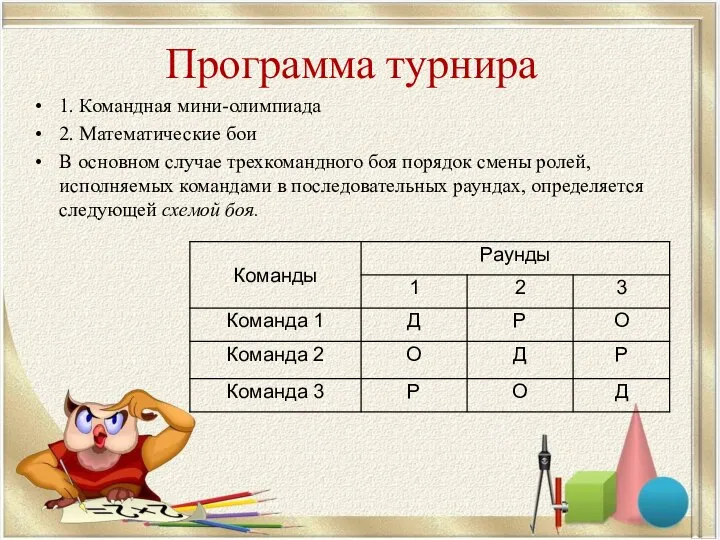
- 18. Программа турнира 1. Командная мини-олимпиада 2. Математические бои В основном случае трехкомандного боя порядок смены ролей,
- 19. Задания командной олимпиады II Гимназический турнир юных математиков «Математический Олимп» «Математическая карусель» Задания командной экспресс-олимпиады 1
- 20. Обобщения 4-й задачи !!! (см. Международный математический Турнир Городов, 6-7 класс, базовый вариант, 7 октября 2012
- 21. 1.1. В седьмом классе некоторой школы каждый мальчик дружит с 5-ю девочками и 6-ю мальчиками, а
- 22. Исследовательская работа по теме: «Переливания 1. Классическая задача о переливаниях» Работу выполнил: Розенберг Максим Ученик 8
- 23. Введение Исходная постановка: даны сосуды объемом 3 и 5 литров. Можно ли при помощи этих сосудов
- 24. Введение Общая постановка: 2) как получить заданное значение с литров (алгоритм)? 3) как быстрее получить заданное
- 25. Основные понятия, определения и обозначения Система сосудов [a;b] Состояние системы (l;m) Элементарная операция Цикл Длина цикла
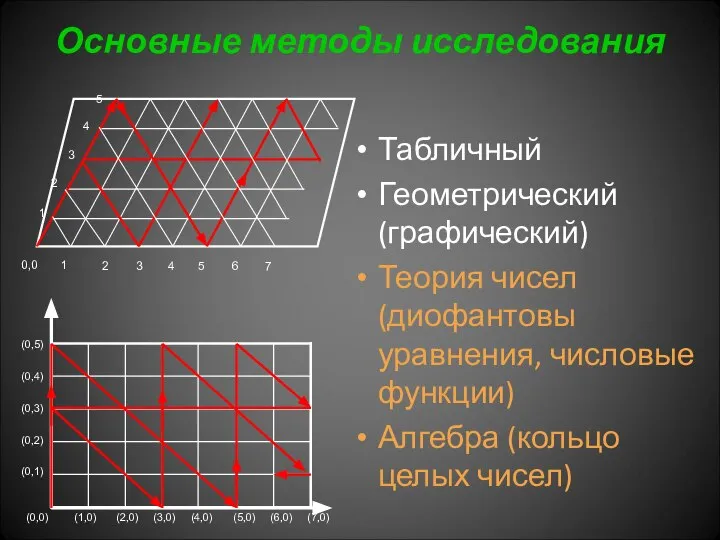
- 26. Основные методы исследования Табличный Геометрический (графический) Теория чисел (диофантовы уравнения, числовые функции) Алгебра (кольцо целых чисел)
- 27. Основные методы исследования Табличный Геометрический (графический) Теория чисел (диофантовы уравнения, числовые функции) Алгебра (кольцо целых чисел)
- 28. 1. Как переливать! При переливаниях с сосудами a и b имеют смысл лишь постоянные последовательные переливания
- 29. НОД(a; b) = 1 Иначе, если a = sd и b = fd, то с обязательно
- 30. Если НОД(a; b) = 1, то можно получить любое значение с литров, где 0 Примечание. Случаи
- 31. 2(a+b)-1 - число состояний 2(a+b)-2 - число элементарных операций (переливаний) 5. Как определить кол-во минициклов? b
- 32. 6. Как определить точное минимальное кол-во операций до искомого кол-ва литров? Структура цикла: А → В:
- 33. 6. Как определить точное минимальное кол-во операций до искомого кол-ва литров? 1) ax-by=c 2) 2(x+y)+1 c>a
- 34. Результаты Таблица. Точное минимальное кол-во операций до искомого кол-ва литров?
- 35. 7. Какова структура цикла? 2([ak/b]-[a(k-1)/b])+2 2([bk/a]-[b(k-1)/a])+2 Результаты
- 36. Итоги Полностью исследован случай двух сосудов Дальнейшие задачи Исследовать замкнутую систему 3-ех сосудов Исследовать не замкнутую
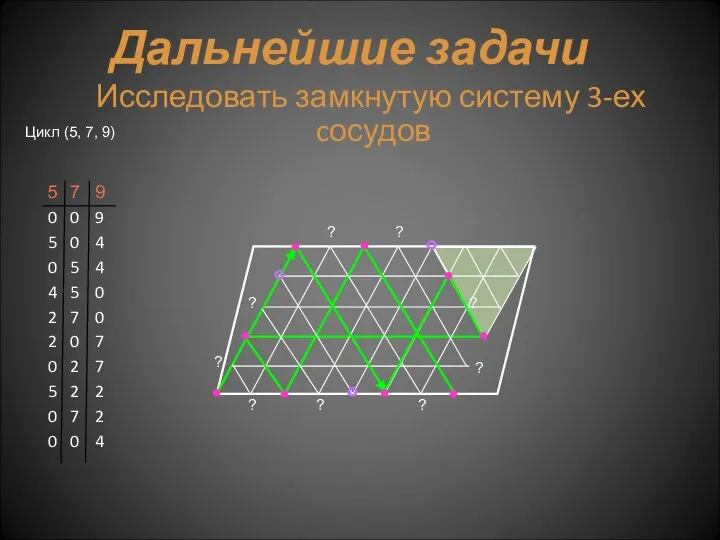
- 37. Цикл (5, 7, 9) Дальнейшие задачи Исследовать замкнутую систему 3-ех cосудов
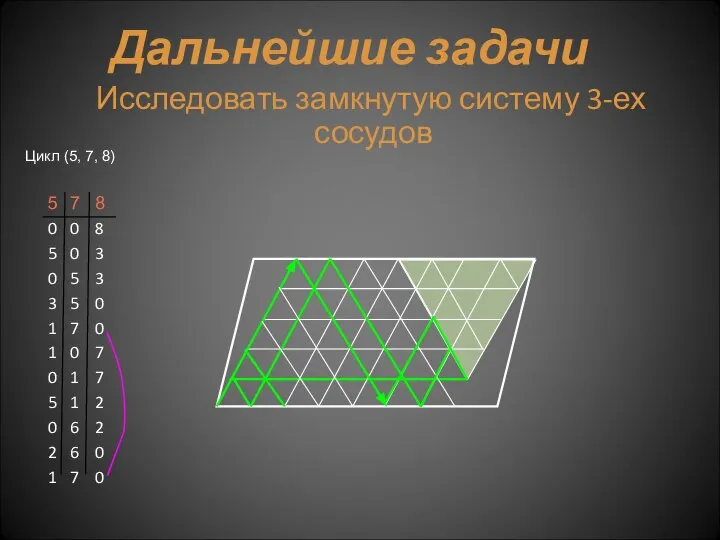
- 38. Цикл (5, 7, 8) Дальнейшие задачи Исследовать замкнутую систему 3-ех сосудов
- 40. Скачать презентацию




















![Основные понятия, определения и обозначения Система сосудов [a;b] Состояние системы (l;m) Элементарная](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1131414/slide-24.jpg)








![7. Какова структура цикла? 2([ak/b]-[a(k-1)/b])+2 2([bk/a]-[b(k-1)/a])+2 Результаты](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1131414/slide-34.jpg)

 Презентация на тему История герба России
Презентация на тему История герба России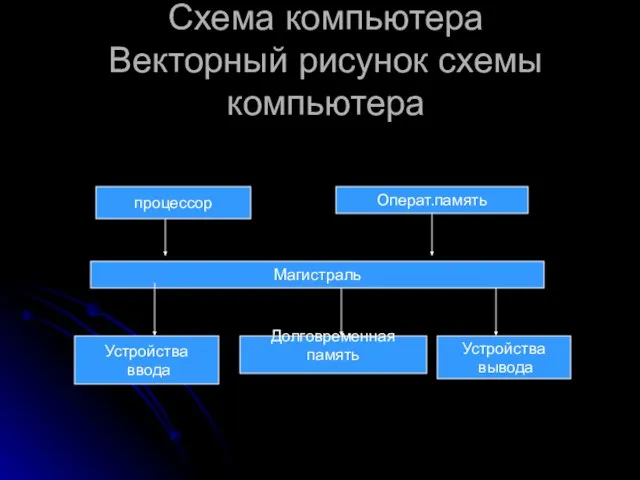 Схема компьютера Векторный рисунок схемы компьютера
Схема компьютера Векторный рисунок схемы компьютера История Масленицы
История Масленицы Президент Российской Федерации (функции и полномочия по Конституции РФ)
Президент Российской Федерации (функции и полномочия по Конституции РФ) www.seo.euvva.com
www.seo.euvva.com Роль отраслевой дипломатии в обеспечении энергетической безопасности
Роль отраслевой дипломатии в обеспечении энергетической безопасности Плотность
Плотность Воспитательная деятельность учителя
Воспитательная деятельность учителя Отработка навыков турпроектирования на основе ценностных ориентиров потребителей
Отработка навыков турпроектирования на основе ценностных ориентиров потребителей Проект «Здоровый образ жизни»
Проект «Здоровый образ жизни» Результаты исследования промо индустрии
Результаты исследования промо индустрии Новый год в открытках Алексея Исакова
Новый год в открытках Алексея Исакова КОКЛЮШ семинар Методические рекомендации по организации профилактических и противоэпидемических мероприятий по коклюшу
КОКЛЮШ семинар Методические рекомендации по организации профилактических и противоэпидемических мероприятий по коклюшу Языковые особенности в Квебеке
Языковые особенности в Квебеке ОРГАНИЗАЦИЯ ИССЛЕДОВАТЕЛЬСКОЙ ДЕЯТЕЛЬНОСТИДЕТЕЙ СТАРШЕГО ДОШКОЛЬНОГО ВОЗРАСТА
ОРГАНИЗАЦИЯ ИССЛЕДОВАТЕЛЬСКОЙ ДЕЯТЕЛЬНОСТИДЕТЕЙ СТАРШЕГО ДОШКОЛЬНОГО ВОЗРАСТА Подготовка к сочинению М. Ю. Лермонтов Мцыри
Подготовка к сочинению М. Ю. Лермонтов Мцыри Видеоадаптеры современных компьютеров
Видеоадаптеры современных компьютеров Планирование и исполнение расходов местных бюджетов РФ (на примере ЗАТО г. Островной Мурманской области)
Планирование и исполнение расходов местных бюджетов РФ (на примере ЗАТО г. Островной Мурманской области) Презентация на тему«Дельфы»
Презентация на тему«Дельфы» Громыко Алексей Олегович Компьютерное моделирование кинематики манипулятора промышленного робота Руководитель: доктор физ.-м
Громыко Алексей Олегович Компьютерное моделирование кинематики манипулятора промышленного робота Руководитель: доктор физ.-м Каша - пища наша
Каша - пища наша Понятие и признаки несостоятельности (банкротства)
Понятие и признаки несостоятельности (банкротства) Развитие угольной промышленности Красноярского края в контексте межрегиональной интеграции
Развитие угольной промышленности Красноярского края в контексте межрегиональной интеграции Фабрика санитарно-гигиенических изделийКрупнейший производитель бумажной санитарно-гигиенической продукции в УкраинеТМ «Неж
Фабрика санитарно-гигиенических изделийКрупнейший производитель бумажной санитарно-гигиенической продукции в УкраинеТМ «Неж Оформим буклет
Оформим буклет Уважаемые Дамы и Господа! Холдинг «Западно-Европейский Финансовый Союз» - динамично развивающаяся группа компаний, предоставляющ
Уважаемые Дамы и Господа! Холдинг «Западно-Европейский Финансовый Союз» - динамично развивающаяся группа компаний, предоставляющ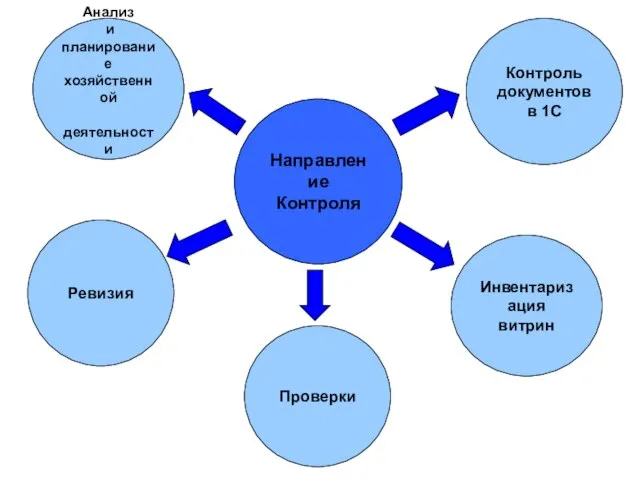 Направление Контроля
Направление Контроля Radical Chic создал платки по мотивам картин Верещагина. Интернет-магазин Третьяковской галереи
Radical Chic создал платки по мотивам картин Верещагина. Интернет-магазин Третьяковской галереи