От показательных уравнений - к показательным неравенствам

"Что значит решить
задачу?
Это значит
свести ее к уже
решенным"
С.А. Яновская

- Какие из данных уравнений являются
показательными?
12)

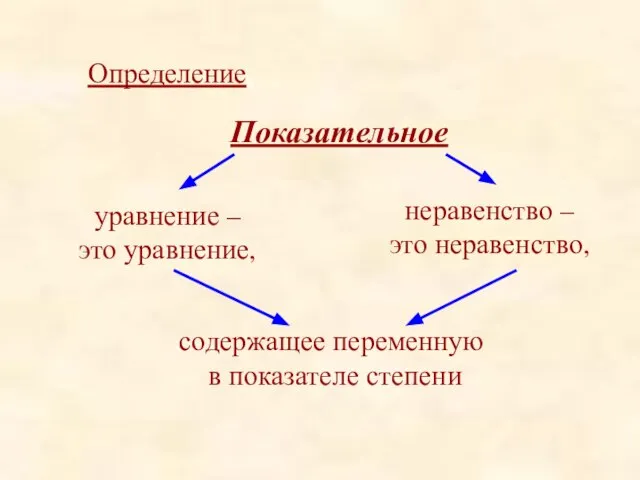
Определение.
Показательное
уравнение –
это уравнение,
неравенство –
это неравенство,
содержащее переменную
в показателе степени

- Каков общий вид простейших показательных уравнений?
- Метод решения?
равносильно уравнению f(x) = g(x)
1.
2.
Обоснование:
Если степени с равными основаниями, отличными от единицы и большими нуля, равны, то показатели равны;
2) функция монотонна на R, поэтому каждое свое значение
она принимает при единственном значении аргумента.
(уравнивание показателей)

- Каков общий вид простейших показательных неравенств?
- Метод решения?
1) Равносильно неравенству f(x) > g(x), а>1
Обоснование:
а) Показательная функция монотонно возрастает (убывает) на R, поэтому большему (меньшему) значению функции соответствует большее значение аргумента.
б) Если a>1, то из неравенства
(сравнение показателей)
2) Равносильно неравенству f(x) < g(x), 0<а<1.
если 0

Работаем устно:
Сравните x и y:
Сравните основание а с единицей:
1.
2.
3.
4.
5.
6.
7.
8.

Решите двойные неравенства:
т.к. показательная функция
с основанием а =5, а>1 возраста-
ет на R, то большему значению
функции соответствует большее
значение аргумента, имеем
Решение.
Ответ: (0;3)
Решение.
т.к. основание степени а = 1/3,
0
Имеем

Функционально-графический метод
решения неравенства f(x) < g(x)
:
1. Подбором найдем корень уравнения f(x)=g(x), используя свойства монотонных функций;
2. Построим схематически графики обеих функций,
проходящие через точку с найденной абсциссой;
3. Выберем решение неравенства, соответствующее
знаку неравенства;
4. Запишем ответ.

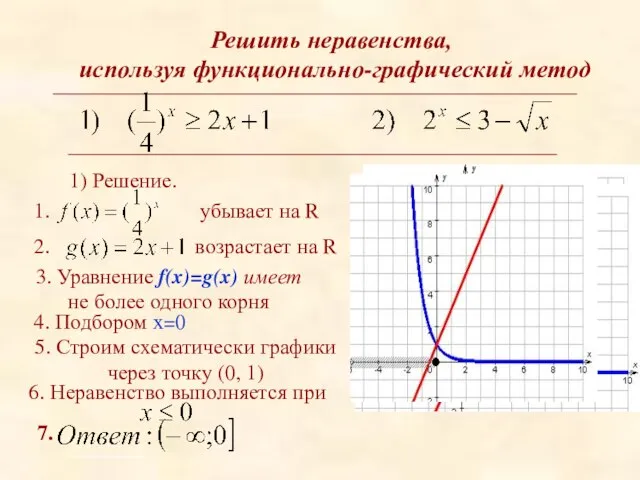
Решить неравенства,
используя функционально-графический метод
1) Решение.
3. Уравнение f(x)=g(x) имеет
не более одного корня
4. Подбором x=0
5. Строим схематически графики
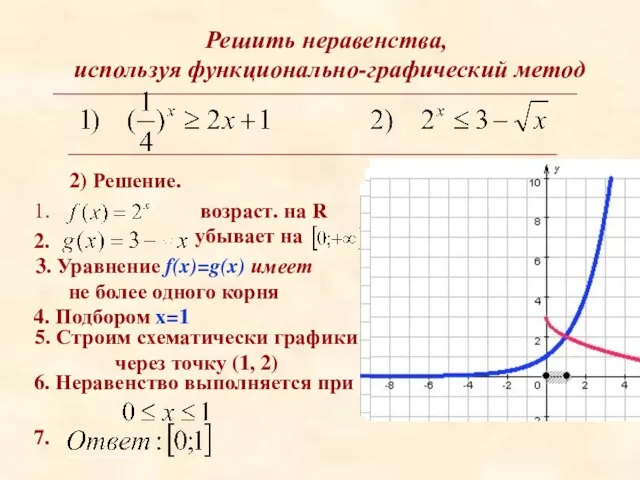
через точку (0, 1)

Решить неравенства,
используя функционально-графический метод
2) Решение.
3. Уравнение f(x)=g(x) имеет
не более одного корня
4. Подбором x=1
5. Строим схематически графики
через точку (1, 2)
6. Неравенство выполняется при

- Каков общий вид простейших показательных неравенств?
- Метод решения?
1) Равносильно неравенству f(x) > g(x), а>1
Обоснование:
а) Показательная функция монотонно возрастает (убывает) на R, поэтому большему (меньшему) значению функции соответствует большее значение аргумента.
б) Если a>1, то из неравенства
(сравнение показателей)
2) Равносильно неравенству f(x) < g(x), 0<а<1.
если 0

«Ключ»
Вариант – 1 Вариант - 2

Задания группам:
1 группа
2 группа
3 группа
4 группа
5 группа
В каждом уравнении замените знак равенства на указанный знак неравенства и решите полученное неравенство.
(Используйте при необходимости метод интервалов).
(>)
( )
(<)
( )
( > )