Содержание
- 2. Оценка доходности банковских операций (методы количественного анализа) Структура курса: Т1: Измерители доходности финансовых операций Т2: Потоки
- 3. Оценка доходности банковских операций (методы количественного анализа) Литература: Четыркин Е.М. Методы финансовых и коммерческих расчетов.-М:Дело, 1998,1999,2003,2008
- 4. Т1: Измерители доходности финансовых операций Вопросы: Т1.1. Измерители доходности. Т1.2. Простые и сложные проценты. Т1.3. Учетная
- 5. Т1: Измерители доходности финансовых операций Т1.1.Измерители доходности.
- 6. Т1: Измерители доходности финансовых операций Т1.1.Измерители доходности.
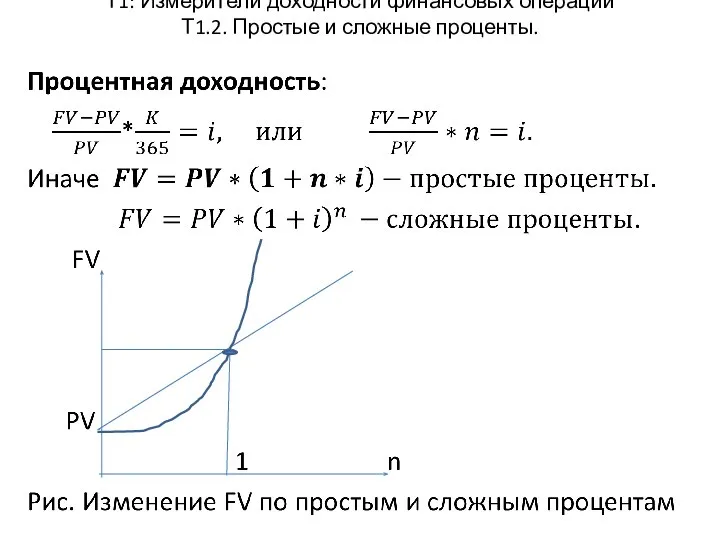
- 7. Т1: Измерители доходности финансовых операций Т1.2. Простые и сложные проценты.
- 8. Т1: Измерители доходности финансовых операций Т1.2. Простые и сложные проценты.
- 9. Т1: Измерители доходности финансовых операций Т1.2 Простые и сложные проценты. .
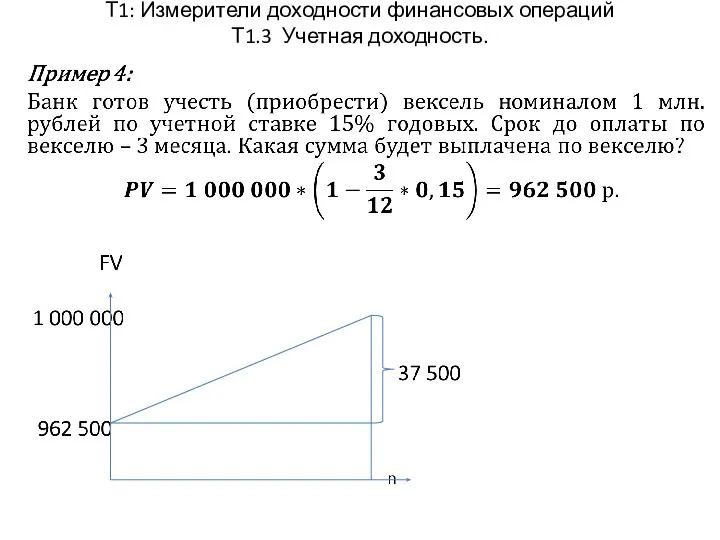
- 10. Т1: Измерители доходности финансовых операций Т1.3 Учетная доходность.
- 11. Т1: Измерители доходности финансовых операций Т1.3 Учетная доходность.
- 12. Т1: Измерители доходности финансовых операций Т1.4. Эквивалентная доходность
- 13. Т1: Измерители доходности финансовых операций Т1.4. Эквивалентная доходность
- 14. Т1: Измерители доходности финансовых операций Т1.5. Эффективная доходность
- 15. Т1: Измерители доходности финансовых операций Т1.5. Эффективная доходность
- 16. Т1: Измерители доходности финансовых операций Т1.5. Эффективная доходность
- 17. Т1: Измерители доходности финансовых операций Т1.6. Учет инфляции в финансовых вычислениях
- 18. Т2: Потоки платежей. Финансовая рента Содержание: Т2.1 Типы финансовых потоков, распределенных во времени Т2.2 Параметры финансовых
- 19. Т2: Потоки платежей. Финансовая рента Т2.1 Типы финансовых потоков, распределенных во времени R1 R1 R1 R1
- 20. Т2: Потоки платежей. Финансовая рента Т2.1 Типы финансовых потоков, распределенных во времени R1 R1 R1 R1
- 21. Т2: Потоки платежей. Финансовая рента Т2.1 Типы финансовых потоков, распределенных во времени Потоки платежей могут быть
- 22. Т2: Потоки платежей. Финансовая рента Т2.2 Параметры финансовых потоков Параметры - элементы, однозначно описывающие финансовый поток.
- 23. Т2: Потоки платежей. Финансовая рента Т2.2 Параметры финансовых потоков В зависимости от момента совершения платежа (в
- 24. Т2: Потоки платежей. Финансовая рента Т2.3 Обобщенные характеристики ренты: Наращенная величина. Современная стоимость Наращенная сумма PV
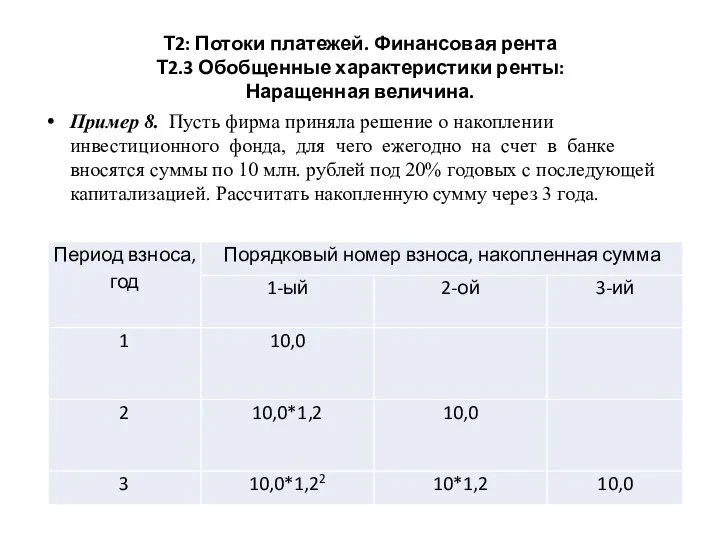
- 25. Т2: Потоки платежей. Финансовая рента Т2.3 Обобщенные характеристики ренты: Наращенная величина. Пример 8. Пусть фирма приняла
- 26. Т2: Потоки платежей. Финансовая рента Т2.3 Обобщенные характеристики ренты: Наращенная величина.
- 27. Т2: Потоки платежей. Финансовая рента Т2.3 Обобщенные характеристики ренты: Современная величина. Под современной стоимостью потока платежей
- 28. Т2: Потоки платежей. Финансовая рента Т2.3 Обобщенные характеристики ренты: Современная величина. Где PV-современная сумма ренты, R
- 29. Т2: Потоки платежей. Финансовая рента Т2.3 Обобщенные характеристики ренты: Современная величина.
- 30. Т2: Потоки платежей. Финансовая рента Т2.3 Расчет параметров ренты Расчет параметров ренты основан на арифметическом расчете
- 31. Т2: Потоки платежей. Финансовая рента Т2.4 Расчет параметров ренты. Метод последовательных приближений для расчета процентной ставки
- 32. Т2: Потоки платежей. Финансовая рента Т2.4 Расчет параметров ренты.
- 33. Методы погашения долгосрочной задолженности Тема 3
- 34. Методы погашения долгосрочной задолженности Методы погашения долгосрочной задолженности Единоразовое погашение Возврат разовым платежом без накопления на
- 35. Методы погашения долгосрочной задолженности Методы погашения долгосрочной задолженности Единоразовое погашение Возврат разовым платежом без накопления на
- 36. Методы погашения долгосрочной задолженности
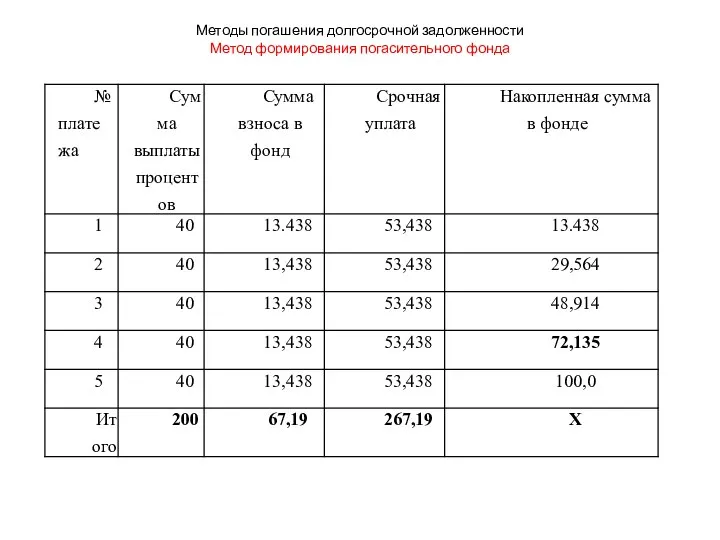
- 37. Методы погашения долгосрочной задолженности Метод формирования погасительного фонда Подставив R в формулу (1), получим Yt =
- 38. Методы погашения долгосрочной задолженности Метод формирования погасительного фонда
- 39. Методы погашения долгосрочной задолженности Метод формирования погасительного фонда
- 40. Методы погашения долгосрочной задолженности Метод формирования погасительного фонда Сумма накопления в фонде Wt рассчитывается наращиванием ежегодных
- 41. Методы погашения долгосрочной задолженности Погашение равными суммами долга При годовом погашении размеры платежей по основному долгу
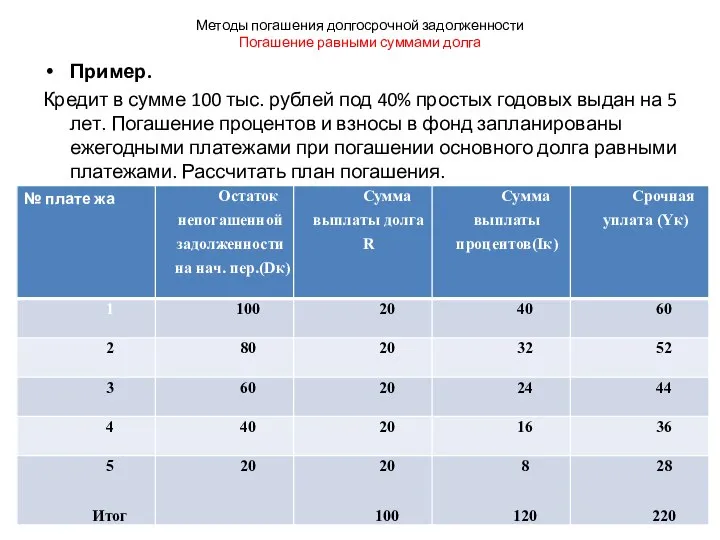
- 42. Методы погашения долгосрочной задолженности Погашение равными суммами долга Пример. Кредит в сумме 100 тыс. рублей под
- 43. Методы погашения долгосрочной задолженности Погашение равными суммами долга Суммы, идущие на погашение долга, увеличиваются во времени:
- 44. Методы погашения долгосрочной задолженности Погашение равными срочными уплатами (аннуитетом)
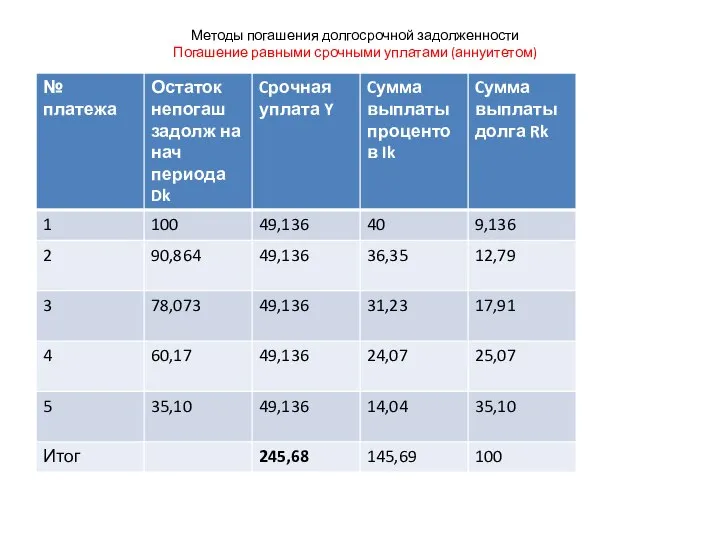
- 45. Методы погашения долгосрочной задолженности Погашение равными срочными уплатами (аннуитетом) Пример Тот же. Погашение равными суммами вместе
- 46. Методы погашения долгосрочной задолженности Погашение равными срочными уплатами (аннуитетом)
- 47. Методы погашения долгосрочной задолженности Погашение равными срочными уплатами (аннуитетом) Суммы, идущие на погашение долга, увеличиваются во
- 48. Методы погашения долгосрочной задолженности Погашение схема «78» Пусть выдан потребительский кредит в сумме D на n
- 49. Методы погашения долгосрочной задолженности Погашение схема «78» Процентные выплаты расположены в последовательности nр/Q, nр-1/Q,...,1/Q. Величина Q
- 50. Методы погашения долгосрочной задолженности Погашение схема «78» Пример. Погашение потребительского кредита ведется в течение 5 лет.
- 52. Скачать презентацию











































 «Настольная кукла»
«Настольная кукла» Форматы графических файлов
Форматы графических файлов Pets and presidents
Pets and presidents Елена Александровна Благинина
Елена Александровна Благинина Легкая атлетика. Определение лёгкой атлетики
Легкая атлетика. Определение лёгкой атлетики Основные требования к кандидатской диссертацииКак написать хорошую диссертацию
Основные требования к кандидатской диссертацииКак написать хорошую диссертацию Презентация на тему Наполеон и Кутузов по Толстому
Презентация на тему Наполеон и Кутузов по Толстому Начертательная геометрия
Начертательная геометрия Межличностные отношения
Межличностные отношения Затратный подход. Метод оценки стоимости объекта с учётом износа
Затратный подход. Метод оценки стоимости объекта с учётом износа Имя числительное (3 класс)
Имя числительное (3 класс) «1С-Отчетность»удобный способэлектронной отчетности
«1С-Отчетность»удобный способэлектронной отчетности Электронная коммерция в туризме
Электронная коммерция в туризме Тундра 3 класс
Тундра 3 класс Многие песни А. Пахмутовой незаметно вошли в нашу жизнь, они активно воздействуют на людей- воспитывают их мысли и чувства, помогаю
Многие песни А. Пахмутовой незаметно вошли в нашу жизнь, они активно воздействуют на людей- воспитывают их мысли и чувства, помогаю Моя республикаТатарстан
Моя республикаТатарстан Понятие, предмет, объект, субъект, история развития муниципального права
Понятие, предмет, объект, субъект, история развития муниципального права Государственная программа "Образование и развитие инновационной экономики: внедрение современной модели образования в 2009 - 2012 г
Государственная программа "Образование и развитие инновационной экономики: внедрение современной модели образования в 2009 - 2012 г Мой любимый детский сад Журавушка
Мой любимый детский сад Журавушка Олимпийский центр «Вентспилс»
Олимпийский центр «Вентспилс» Использование результатов ОГЭ и ЕГЭ в повышении качества образования по иностранному языку
Использование результатов ОГЭ и ЕГЭ в повышении качества образования по иностранному языку Молодіжні субкультури
Молодіжні субкультури УЧИТЕЛЯ
УЧИТЕЛЯ Презентация на тему Продажа имения старой графини» математическая игра для10-11 классов
Презентация на тему Продажа имения старой графини» математическая игра для10-11 классов  Что в имени тебе моем...?
Что в имени тебе моем...? dr
dr Мастер-класс по изготовлению куклы-дергунчика
Мастер-класс по изготовлению куклы-дергунчика Водоросли
Водоросли