Оценка неопределенности результатов экстракционного атомно-абсорбционного анализа

Расчет неопределенности по типу Б
Процедура оценивания неопределенности результатов измерений по типу Б :
определяется измеряемая величина;
определяются источники неопределенности при проведении измерений, вносящие свой вклад в значение измеряемой величины для каждого конкретного случая;

проводится количественная оценка составляющих неопределенности;
вычисляется суммарная неопределенность найденных составляющих неопределенности;
определяются значимые составляющие при необходимости повторной оценки.

Измерительная задача
Необходимо определить массовую концентрацию Cd в образце керамической посуды.
Метод основан на извлечении Cd из образца керамической посуды раствором уксусной кислоты при 22±2оС и последующим измерением плотности атомной абсорбции раствора. Интенсивность плотности атомной абсорбции пропорциональна массовой концентрации Cd в образце.
Плотность атомной абсорбции измеряют с помощью атомно-абсорбционного спектрофотометра. Массовую концентрацию определяемого ингредиента Cd находят по градуировочному графику.

Условия проведения испытаний
Пусть ….
Образец доводят до температуры (22 ± 2) °С.
Определяют площадь поверхности образца.
Образец заполняют 4 % (об.) раствором уксусной кислоты при (22 ± 2) °С в пределах 1 мм до уровня перелива, измеренного от верхнего края образца.
Объем использованной 4 % уксусной кислоты определяют с точностью ±2% (332 мл).
Образец выдерживают при (22 ± 2) °С в течение 24 часов в темноте для предотвращения потерь вследствие испарения.

Условия проведения испытаний
Необходим исходный раствор кадмия с массовой концентрацией (500 ± 0,5) мг/л в 4 % (об.) уксусной кислоте.
Свежеприготовленный 4 % (об.) раствор уксусной кислоты готовят разбавлением 40 мл ледяной уксусной кислоты до 1 л дистиллированной водой.
Стеклянная лабораторная посуда не ниже класса В, несодержащая кадмия.
Атомно-абсорбционный спектрофотометр должен иметь пределы обнаружения не хуже 0,02 мг/л по кадмию.

Условия проведения испытаний
После выдерживания раствор перемешивают для однородности, отбирают пробу, при необходимости разбавляя ее в d раз, и анализируют методом ААС по градуировочной кривой, построенной методом наименьших квадратов.
Вычисленный результат представляют как общее количество кадмия в объеме выщелачивающего раствора, выраженное в мг/дм2 кадмия.

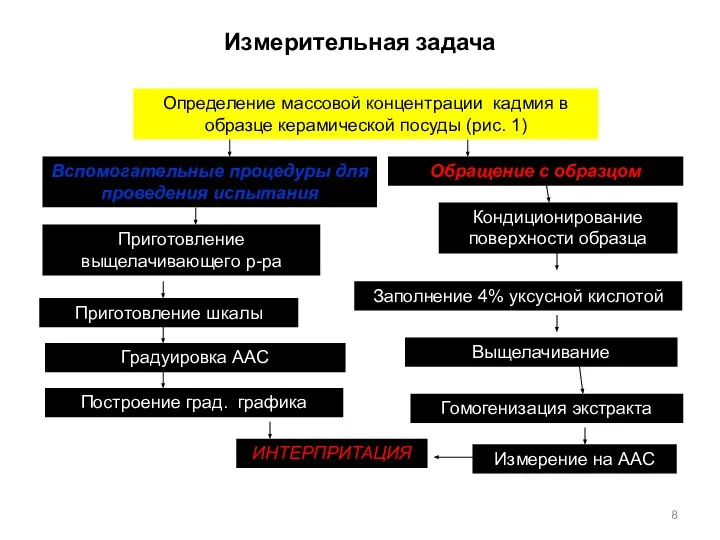
Измерительная задача
Определение массовой концентрации кадмия в образце керамической посуды (рис. 1)
Вспомогательные процедуры для проведения испытания
Обращение с образцом
Гомогенизация экстракта
Кондиционирование поверхности образца
Заполнение 4% уксусной кислотой
Приготовление выщелачивающего р-ра
Измерение на ААС
ИНТЕРПРИТАЦИЯ
Приготовление шкалы
Градуировка ААС
Построение град. графика
Выщелачивание

Математическая модель
Массовая концентрация Cd пробе:
(1)
Co Содержание Cd в выщелачивающем растворе, мг/л
d Коэффициент разбавления (при необходимости)
Vt Объем выщелачивающего раствора, л
av Площадь поверхности сосуда, дм2
r Масса выщелачиваемого кадмия на единицу площади, мг/дм2
Рассмотрим величины, входящие в уравнение и оценим их неопределенности.

Выявление и анализ источников неопределенности
Смещение, обусловленное методом, принято равным нулю, т.к. метод используется в заданной области применения. Т.к. в данном примере нет аттестованного образца сравнения, то общий контроль смещения сводится к контролю тех параметров метода, которые влияют на результат. Такими влияющими величинами являются время и температура выщелачивания, концентрация (масса, объем), измерение площади и разбавление.

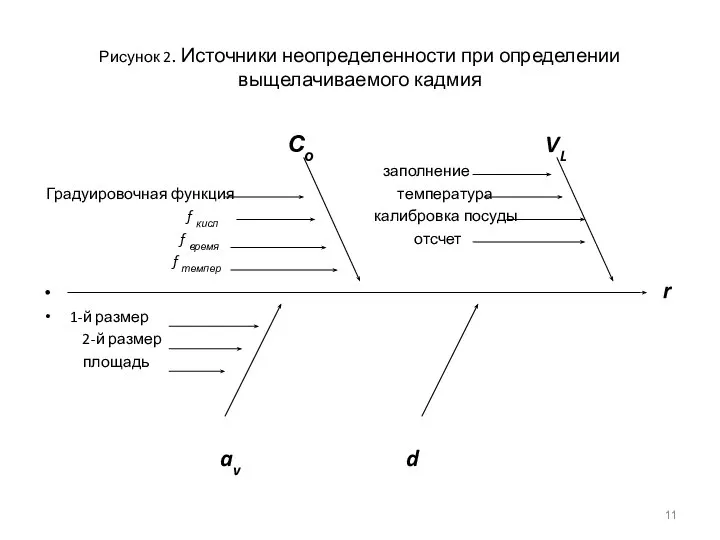
Рисунок 2. Источники неопределенности при определении выщелачиваемого кадмия
Со VL
заполнение
Градуировочная функция температура
f кисл калибровка посуды
f время отсчет
f темпер
r
1-й размер
2-й размер
площадь
av d

С учетом рассмотренных факторов массовая концентрация Cd (мг/дм-2)пробе будет:
(2)
Co Содержание Cd в выщелачивающем растворе, мг/л
d Коэффициент разбавления (при необходимости)
VL Объем выщелачивающего раствора, л
av Площадь поверхности сосуда, дм2
f кисл Влияние концентрации кислоты

f время Влияние времени выщелачивания
f темп Влияние температуры выщелачивания

Количественное описание источников неопределенности измерения объема
Заполнение: Описание метода требует, чтобы сосуд заполнялся "в пределах 1 мм от края". Для обычной посуды 1 мм пусть будет представлять около 1% высоты сосуда. Таким образом, сосуд будет заполнен на (99,5 ± 0,5)% (т.е. заполнение будет равно 0,995 ±0,005 объема сосуда). Пусть объем раствора будет VL = 332 мл
Стандартная неопределенность заполнения рассчитывается в предположении треугольного распределения, т.е. 0,005* VL /√6 мл = 0,005*332/√6 мл

Количественное описание источников
неопределенности измерения объема
Температура: Температура выщелачивающего раствора должна быть (22 ± 2) °С. Стандартная неопределенность объема (332 мл), которая обусловлена объемным расширением жидкости, численно превышающим объемное расширение сосуда, в предположении прямоугольного распределения температуры равна:
21*10-4 * 332 * 2
u(Vt) = ----------------------- = 0,08 мл (3)
√3

Количественное описание источников
неопределенности измерения объема
Отсчет: Используемый объем VL должен быть определен в пределах 2%. На практике применение мерного цилиндра позволяет получить точность в пределах 1% (т.е. 0,01VL). Стандартная неопределенность отсчета рассчитывается в предположении треугольного распределения, т.е.
0,01* VL /√6 мл.
Калибровка: В соответствии с техническими требованиями производителя мерной посуды для мерного цилиндра на 500 мл отклонения составляют ±2,5 мл. Стандартную неопределенность калибровки находят в предположении треугольного распределения, т.е . 2,5/√6 мл

Неопределенность, обусловленная измерением объема
Четыре составляющие неопределенности (Влияние Заполнения, Температуры, Отсчета, Калибровки) суммируют по формуле:
(4)

Неопределенность определения концентрации Неопределенность u(Со), связанная с процедурой построения графика методом наименьших квадратов
Концентрацию выщелоченного кадмия в уксусной кислоте определяют методом ААС и находят с помощью построенной градуировочной линейной зависимости по формуле:
Аo – a
Сo = --------------- мг/л (5)
B

Неопределенность определения концентрации Неопределенность построения графика методом наименьших квадратов
где:
Со - массовая концентрация кадмия в выщелачивающем растворе, мг/л;
Ао - оптическое поглощение металла;
a - точка пересечения линейного градуировочного графика с осью ординат;
b - наклон линейного градуировочного графика, л/мг.

Неопределенность определения концентрации Неопределенность построения графика методом наименьших квадратов
Градуировочный график строят методом наменьших квадратов
С целью построения градуировочной кривой были приготовлены 5 градуировочных растворов с концентрациями: 0,1; 0,3; 0,5; 0,7; 0,9 мг/л из исходного раствора с концентрацией кадмия (500 ± 0,5) мг/л.
Оптическое поглощение каждого из пяти градуировочных растворов измеряли по 3 раза.

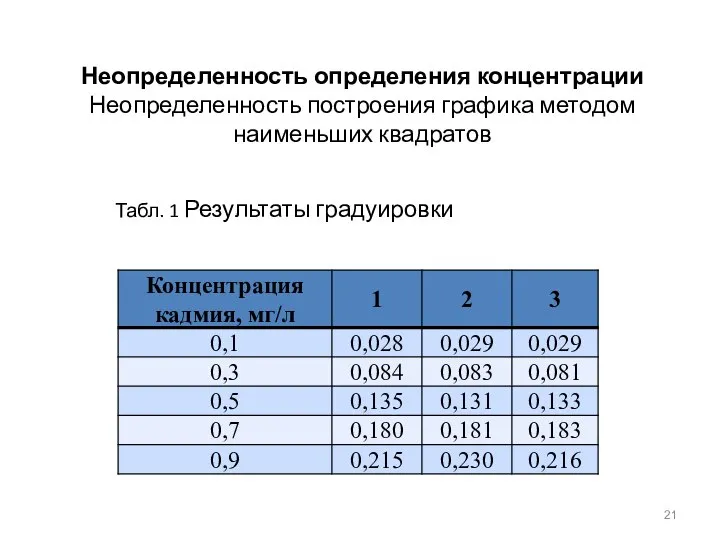
Неопределенность определения концентрации Неопределенность построения графика методом наименьших квадратов
Табл. 1 Результаты градуировки

Неопределенность определения концентрации Неопределенность построения графика методом наименьших квадратов
Линейный метод наименьших квадратов предполагает, что неопределенности значений абсцисс значительно меньше, чем неопределенности значений ординат. Поэтому обычные методы расчета неопределенности Со отражают лишь неопределенности поглощения. Они не учитывают неопределенности концентрации растворов для градуировки, и корреляции, вызванной последовательным разбавлением исходного раствора. Неопределенности градуировочных растворов достаточно малы, и ими можно пренебречь (см. неопределенность колориметрических методов).

Неопределенность определения концентрации Неопределенность построения графика методом наименьших квадратов
Градуировочная функция дается уравнением:
A = a + b * C, (6)
где:
А – атомно-абсорбционное поглощение раствора;
С - концентрация металла в растворе;
a - точка пересечения линейного градуировочного графика с осью ординат;
b - угловой коэффициент линейного градуировочного графика.

Величину r определяем путем подстановки значений Со из уравнения (6):
(Аo – a) * VL
r = -------------------------- * d мг/дм2 (7)
av* b

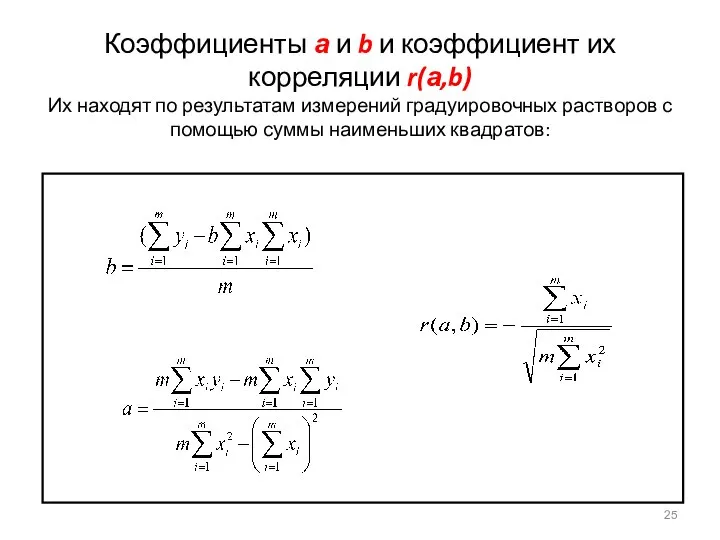
Коэффициенты а и b и коэффициент их корреляции r(а,b)
Их находят по результатам измерений градуировочных растворов с помощью суммы наименьших квадратов:

Неопределенность определения концентрации
Коэффициенты а и b и коэффициент их корреляции r(а,b)
где m – количество пар точек, используемых для построения графика (количество градуировочных растворов, умноженное на число повторных измерений, выполненных для каждого из них);
xi – концентрация кадмия в i -ом градуировочном растворе, мг/дм3,
yi – измеренная оптическая плотность i -ого градуировочного раствора, D;
i – индекс точки, i =1, 2,..., m.

Неопределенность, вызванная измерением концентрации
Коэффициенты а и b и коэффициент их корреляции r(а,b)
Из табл. 1 результаты статистического анализа с применением метода наименьших квадратов с таковы:
b = 0,2410,
a = 0,0087
r = 0,997 (коэффициент корреляции).
Оптическое поглощение раствора после выщелачивания измеряли дважды.
Пусть в результате по градуировочному графику получено значение концентрации кадмия
Cо = 0,26 мг/л

Неопределенность определения концентрации u(Со), связанной с построением графика методом наименьших квадратов.
Стандартную неопределенность и(Со) рассчитываем по формуле:
(8)
где
р - число измерений при определении Сo
n - общее число измерений при градуировке (число градуировочных р-ров, умноженное на число измерений, каждого из них);
Co - найденное значение концентрации кадмия в растворе после выщелачивания;

Неопределенность определения концентрации u(Со), связанной с построением графика методом наименьших квадратов.
Ccp - среднее значение концентрации для градуировочных растворов;
i - общий индекс измерения при градуировке.
S – остаточное стандартное отклонение, которое равно:
= 0,005486 (9)

Sxx = Σ(ci -cср )2 = 1,2 (10)
Рассчитаем u(Со), подставляя в формулу (8) вычисленные значения:
= 0,018мг/л (11)

Влияние температуры fтемп
Принято, что фактор влияния температуры fтемп = 1 [GUM]
Было установлено, что изменение количества выделяющегося металла с изменением температуры вблизи 25 °С является приблизительно линейным, и градиент равен примерно 5% на градус Цельсия [GUM].
При условии, что методика допускает отклонения температуры в пределах ±2°С, это приводит к коэффициенту fтемп = 1 ± 0,1 (т.к. 0,05*2=0,1).
Стандартная неопределенность влияния температуры в предположении прямоугольного распределения бует:
u( fтемп) = 0,1 / √3 = 0,06.

Влияние времени выщелачивания fвремя
Принято, что фактор влияния времени fвремя = 1 [GUM]
Для медленного процесса выщелачивания количество экстрагируемого металла примерно пропорционально продолжительности выщелачивания. Установлено [GUM], что среднее изменение концентрации на протяжении последних 6 часов выщелачивания составляет около 1,8мг/л на уровне 86мг/л, т.е. около 0,3% в час. Поэтому для времени (24 ± 0,5) час в уравнение измерений необходимо ввести поправочный множитель fвремя = 1 ± (0,5 x 0,003) = 1± 0,0015.
При прямоугольном распределении стандартная неопределенность фактора времени будет:
u( fвремя) = 0,0015 / √3 = 0,001.

Влияние концентрации кислоты fкислот
Исследование влияния концентрации кислоты на выделение кадмия показало, что изменение объемной доли кислоты от 4 до 5% увеличивает его выделение с 92,9 до 101,9 мг/л, т.е. вызывает изменение fкислот равное (101,9 - 92,9)/92,9 = 0,097, ~ 0,1 [GUM].
Если принять приблизительно линейную зависимость выделения металла от концентрации кислоты, это дает оценку изменения fкислот примерно 0,1 на 1 % изменения объемной доли кислоты [GUM].

Влияние концентрации кислоты fкислот
Объемная доля кислоты (4 %) и ее стандартная неопределенность (0,008 %) были установлены в отдельном эксперименте с помощью титрования стандартизованным раствором NaOH [GUM].
Исходя из неопределенности 0,008 % получаем неопределенность для fкислот равную 0,008 * 0,1 =0,0008. Т.к. неопределенность объемной доли кислоты уже выражена в виде стандартной неопределенности, полученное значение можно прямо использовать как неопределенность, связанную c fкислот, т.е
u(fкислот) = 0,0008

Неопределенность, обусловленная измерением полезной площади образца аv
Измерения длин для вычисления полезной площади образца:
Площадь полезной поверхности сосуда вычислена, исходя из его размеров. При условии, что образец имеет цилиндрическую форму необходимо для вычисления площади измерить его внутреннюю высоту и внутренний диаметр. Точность линейных измерений оценена в пределах 2 мм (т.е. 0,02дм) при 95 % достоверности [GUM]. При нормальном распределении это ведет к оценке стандартной неопределенности линейных измерений равной 0,02/1,96 = 0,01 дм [GUM].

Неопределенность, обусловленная измерением полезной площади образца аv
Вычисление Площади: Т.к. образец имеет не точную геометрическую (цилиндрическую) форму, то имеется неопределенность, связанная с вычислением площади. Предполагаем, что это дает дополнительно 5% вклада в погрешность определения площади при 95% достоверности. Пусть полезная площадь равна 2,37 дм2.
Составляющие неопределенности линейных измерений и площади суммируют обычным образом:
дм2 (12)

Неопределенность, вызванная
разбавлением испытуемого раствора
Коэффициент разбавления d: В данном примере разбавление не применялось, поэтому d = 1.
Т.к. разведение не проводилось, то неопределенность, вызванная разбавлением = 0.

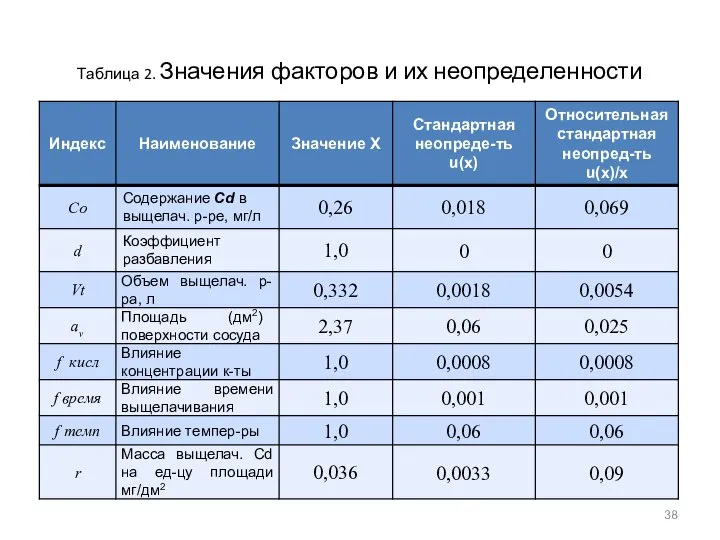
Таблица 2. Значения факторов и их неопределенности

Количество выщелачиваемого кадмия
на единицу площади
Используя формулу (1), промежуточные значения влияющих факторов и их стандартные неопределенности, представленные в табл. 2, получим:
0,26 * 0,332
r = ---------------------- * 1 * 1 * 1 * 1 = 0,034мг/дм2
2,37

Суммарная стандартная неопределенность uc(r)/r
Для вычисления суммарной стандартной неопределенности суммируют стандартные неопределенности для каждой составляющей
_____________________________
= √0,0692 + 0,0542 + 0,0252 + 0,00082 + 0,0012 + 0,062 = 0,095 (13)
Отсюда:
u(r) = 0,095 r = 0,0034 мг/дм2

Расширенная неопределенность
Расширенную неопределенность Ur получают путем умножения стандартной неопределенности массовой концентрации кадмия в пробе воды u(r) на коэффициент охвата k = 2 в предположении нормального распределения для уровня доверия 95 %:
Ur = k * u(r) = 2* u(r) = 2 * 0,0034 = 0,007 мг/дм2