Параллельные прямые

Теорема
Теорема Теорема Теорема
Об аксиомах геометрии
А на чём основаны доказательства самых первых теорем геометрии?
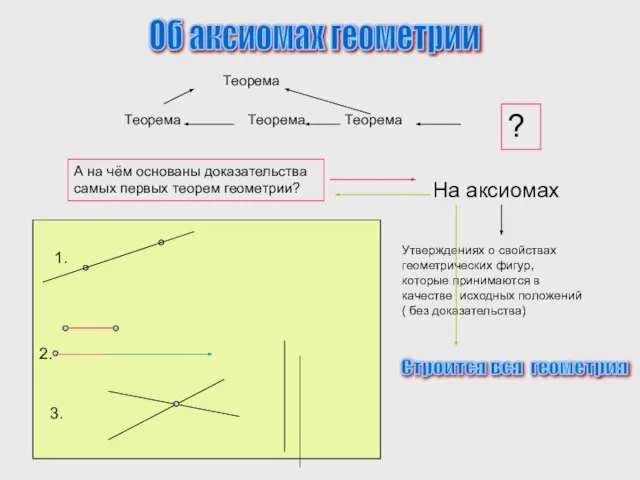
На аксиомах
Утверждениях о свойствах геометрических фигур, которые принимаются в качестве исходных положений ( без доказательства)
2.
?
1.
3.
Строится вся геометрия

Сначала формулируются исходные положения - аксиомы
На их основе, путём логических рассуждений доказываются другие утверждения
Такой подход к построению геометрии зародился в глубокой древности и был изложен в сочинении «Начала» древнегреческого учёного Евклида
365 – 300 гг. до н.э.
Геометрия, изложенная в «Началах», называется евклидовой геометрией
Некоторые из аксиом Евклида (часть из них он называл постулатами) и сейчас используются в геометрии
Слово «аксиома» происходит от греческого «аксиос», что означает «ценный, достойный».

Аксиома параллельных прямых
М
а
в
с
Докажем, что через точку М можно провести прямую, параллельную прямой а.
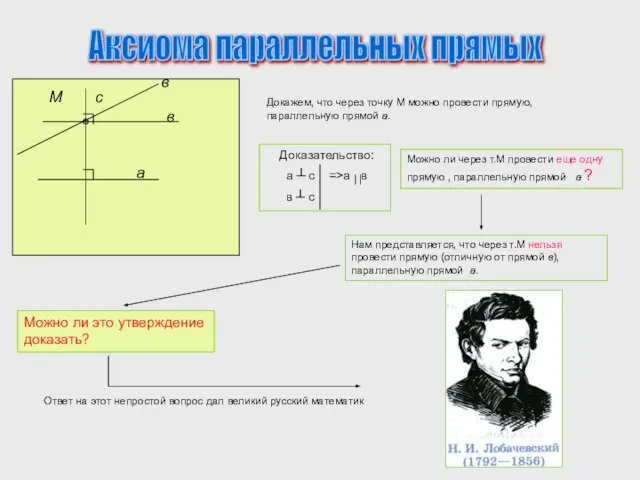
Доказательство:
а ┴ с =>а в
в ┴ с
Можно ли через т.М провести еще одну прямую , параллельную прямой а ?
в
Нам представляется, что через т.М нельзя провести прямую (отличную от прямой в), параллельную прямой а.
Можно ли это утверждение доказать?
Ответ на этот непростой вопрос дал великий русский математик

1. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
2.Если две прямые параллельны третьей прямой, то они параллельны.
Следствия из аксиомы параллельных прямых
а
в
М
с
Доказательство:
Предположим, что прямая с не пересекает прямую в, значит, с в.
Тогда через т.М проходят две прямые а и с параллельные прямой в.
3. Но это противоречит аксиоме параллельных прямых, значит, прямая с пересекает прямую в.
а
в
с
Доказательство:
Предположим, что прямая а и прямая в пересекаются.
2. Тогда через т.М проходят две прямые а и в параллельные прямой с
3 . Но это противоречит аксиоме параллельных прямых.
4. Значит прямые а и в параллельны.
Способ рассуждения,, который называется
методом доказательства от противного