Содержание
- 2. Цель урока: Дать учащимся систематические сведения о параллельных прямых в пространстве.
- 3. Знать и уметь: Основные свойства плоскости. Некоторые следствия из аксиом. Взаимное расположение двух прямых в пространстве.
- 4. Ход урока. Организационный момент. Учебники, тетради, инструменты. Основные задачи курса.
- 5. 2. Домашнее задание. Самостоятельная работа с последующей проверкой. (тесты на парте.) Тест №1 В 2 В
- 6. В 2 В 3 № задания - Ответ № задания - Ответ А1 - 4 А1
- 7. 3. Новый материал: Расположение двух прямых в пространстве. Они могут лежать в одной плоскости или в
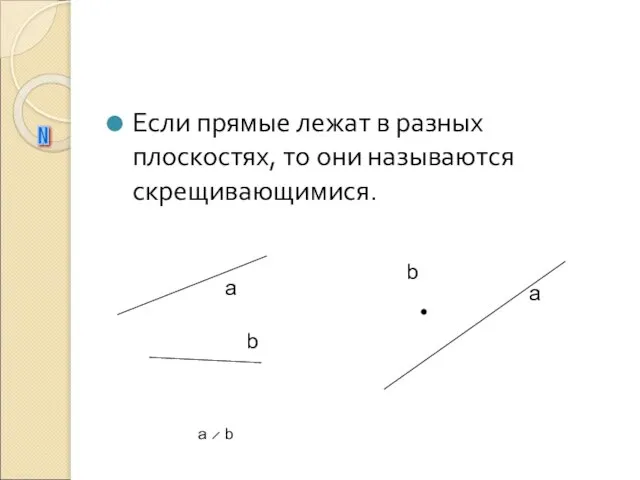
- 8. Если прямые лежат в разных плоскостях, то они называются скрещивающимися. N b a a b а
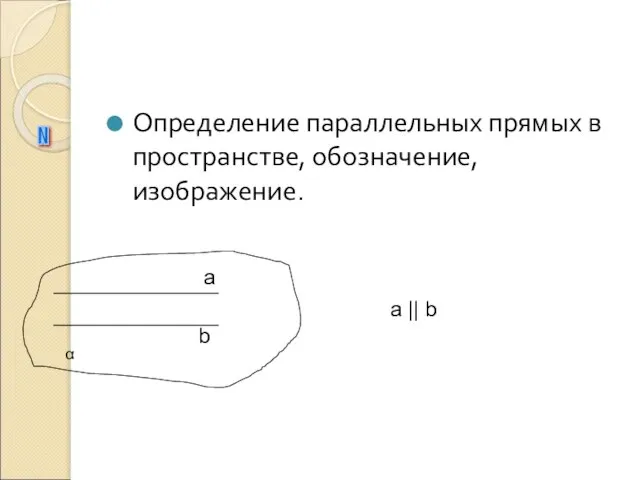
- 9. Определение параллельных прямых в пространстве, обозначение, изображение. N b a α a || b
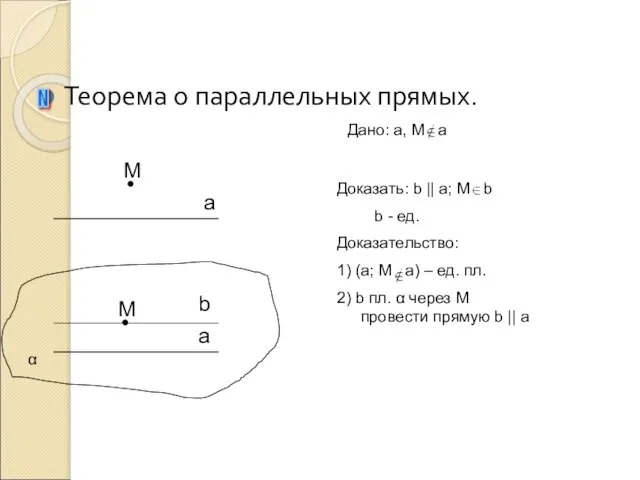
- 10. Теорема о параллельных прямых. N а a α M Дано: a, M a Доказать: b ||
- 11. Лемма о пересечении плоскости параллельными прямыми. (учебник стр.10) N
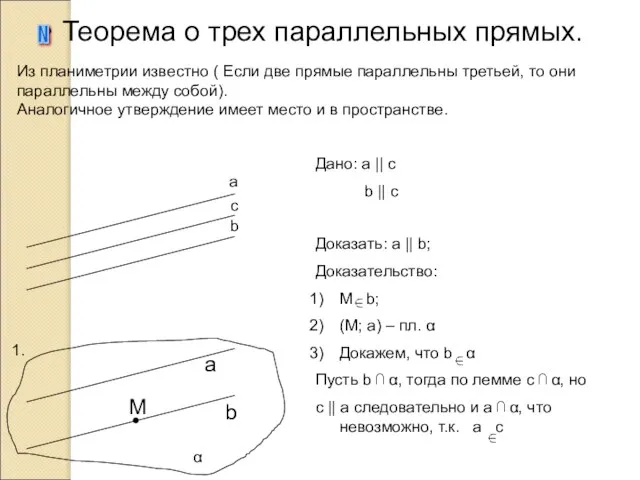
- 12. Теорема о трех параллельных прямых. N a b c b α 1. M a Дано: а
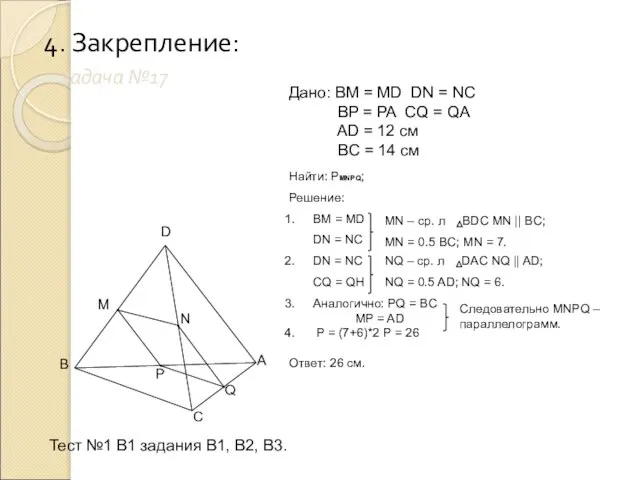
- 13. 4. Закрепление: задача №17 B M D C A N P Q Дано: BM = MD
- 15. Скачать презентацию







 New Year Merry Christmas
New Year Merry Christmas Компания DominiSoft www.dominisoft.ru Компания “БУКА” www.buka.ru www.bukasoft.ru
Компания DominiSoft www.dominisoft.ru Компания “БУКА” www.buka.ru www.bukasoft.ru ЗДОРОВЬЕСБЕРЕГАЮЩИЕ ТЕХНОЛОГИИ, КАК ВЗАИМОДЕЙСТВИЕ УЧЕНИКА И УЧИТЕЛЯ.
ЗДОРОВЬЕСБЕРЕГАЮЩИЕ ТЕХНОЛОГИИ, КАК ВЗАИМОДЕЙСТВИЕ УЧЕНИКА И УЧИТЕЛЯ. Презентация на тему природа коми края
Презентация на тему природа коми края Синдром эмоционального выгорания
Синдром эмоционального выгорания Система образования и проблемы её структуры
Система образования и проблемы её структуры Волейбол. 5-7 классы
Волейбол. 5-7 классы Война — жесточе нету слова,Война — печальней нету слова. Война — святее нету слова В тоске и славе этих лет.И на устах у нас иного
Война — жесточе нету слова,Война — печальней нету слова. Война — святее нету слова В тоске и славе этих лет.И на устах у нас иного Евгений Львович Шварц (1896-1958)
Евгений Львович Шварц (1896-1958) Водоёмы нашей местности
Водоёмы нашей местности Фармакоэпидемиологические и фармакоэкономические аспекты нежелательных реакций лекарственных препаратов – неявная проблема и
Фармакоэпидемиологические и фармакоэкономические аспекты нежелательных реакций лекарственных препаратов – неявная проблема и  Зиянкестердің экономикалық шекті. Зиянын табиғи жауларының тиімділігінің деңгейін анықтау. (Лекция 15)
Зиянкестердің экономикалық шекті. Зиянын табиғи жауларының тиімділігінің деңгейін анықтау. (Лекция 15) Séjour d’études linguistiques Découverte de la Provence
Séjour d’études linguistiques Découverte de la Provence Символи України. Національний український одяг
Символи України. Національний український одяг Законы развития теории судебной экспертизы
Законы развития теории судебной экспертизы Командный проект. Бизнес-задача
Командный проект. Бизнес-задача Взаимодействие с заинтересованными сторонами при подготовке интегрированных отчетов
Взаимодействие с заинтересованными сторонами при подготовке интегрированных отчетов Экономить - значит зарабатывать! Плакат для рабочих
Экономить - значит зарабатывать! Плакат для рабочих Что такое деятельность
Что такое деятельность Микеланджело
Микеланджело  Лучший центр. Белорецк. Скалодром
Лучший центр. Белорецк. Скалодром Здоровьесберегающие технологии в образовательном процессе. Подготовил: зам.директора по УВР Павлов В.В.
Здоровьесберегающие технологии в образовательном процессе. Подготовил: зам.директора по УВР Павлов В.В. Лекция 5. Проблема психологического контроля и управления спортивной деятельностью
Лекция 5. Проблема психологического контроля и управления спортивной деятельностью Опорные схемы и рисунки в помощь учащимся
Опорные схемы и рисунки в помощь учащимся Топология компьютерных сетей
Топология компьютерных сетей Процессоры фирм Intel и AMD
Процессоры фирм Intel и AMD Стили в одежде
Стили в одежде «1С:Предприятие 8. Управление водоканалом»
«1С:Предприятие 8. Управление водоканалом»