Слайд 2При пересечении поверхностей двух многогранников образуется замкнутая ломаная пространственная линия. Ломаная линия

пересечения состоит из отрезков прямых линий. Каждый отрезок представляет собой линию, по которой пересеклась грань одного многогранника с гранью второго многогранника. Вершины ломаной линии представляют собой точки, в которых пересеклись ребра одного многогранника с гранями или ребрами другого.
Слайд 4Поверхность одного многогранника может проходить сквозь поверхность другого многогранника полностью или частично.
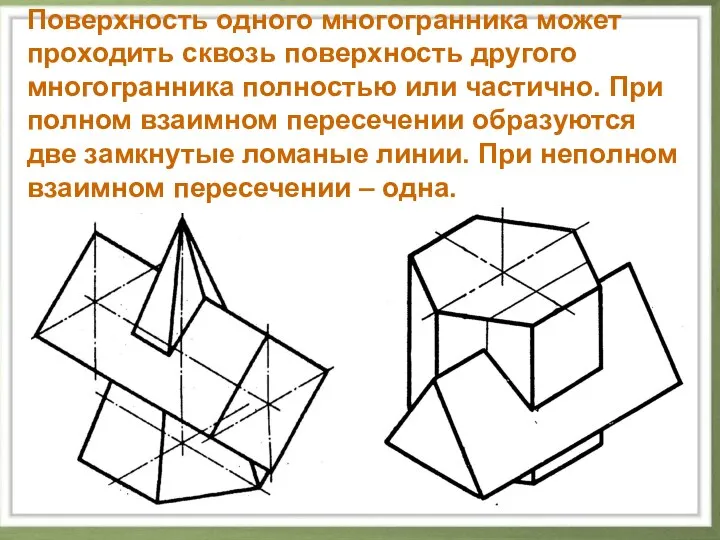
При полном взаимном пересечении образуются две замкнутые ломаные линии. При неполном взаимном пересечении – одна.
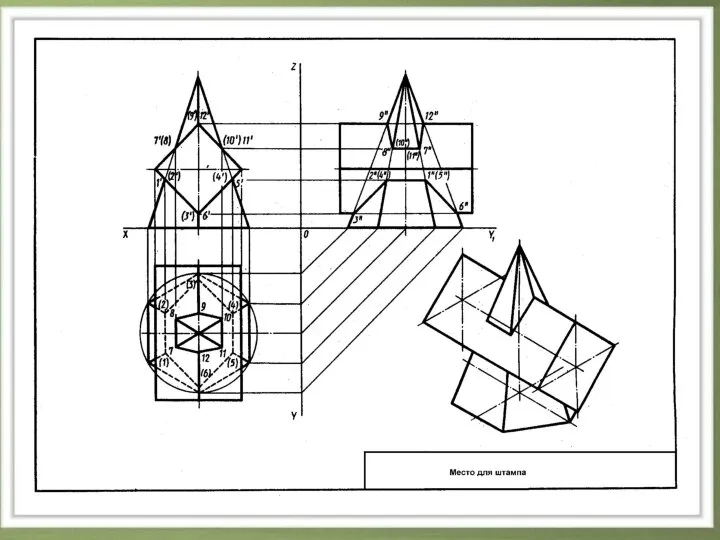
Слайд 5Алгоритм построения линии взаимного пересечения двух многогранников:
Определить тип линии.
Найти точки пересечения ребер

двух многогранников (как пересечение двух прямых).
Найти точки пересечения ребер первого многогранника с гранями второго многогранника и ребер второго многогранника с гранями первого многогранника (решение задачи сводится к построению точки пересечения прямой с плоскостью).
Найденные точки последовательно соединить прямыми линиями.
Определить видимость линии пересечения.



 Принципы организации и деятельности прокуратуры РФ
Принципы организации и деятельности прокуратуры РФ Последствия извержения вулканов. Защита населения
Последствия извержения вулканов. Защита населения Организация хранения данных с использованием системы eDocLib
Организация хранения данных с использованием системы eDocLib Таро расклады
Таро расклады Политические аспекты защиты информации
Политические аспекты защиты информации Словообразование в китайском языке
Словообразование в китайском языке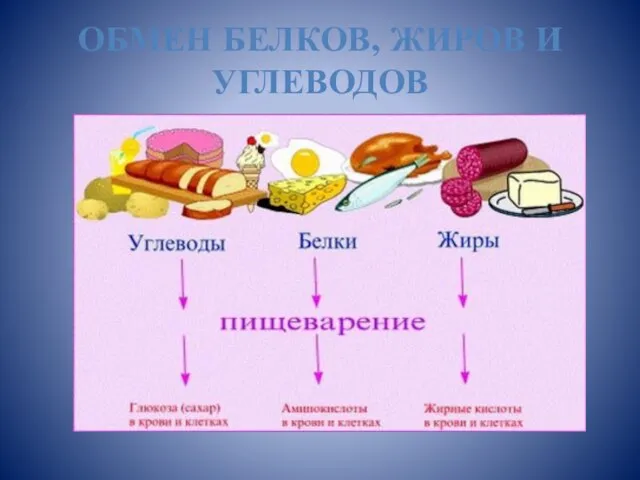 Презентация на тему Обмен белков, жиров и углеводов
Презентация на тему Обмен белков, жиров и углеводов  История газеты
История газеты Арт фестиваль All is Art. Проект
Арт фестиваль All is Art. Проект Упаковочные материалы
Упаковочные материалы Краеведение Экология Автор проекта : Ашанина С.Ю. Подробнее о проекте Смотри «Визитка»
Краеведение Экология Автор проекта : Ашанина С.Ю. Подробнее о проекте Смотри «Визитка» Предпринимательская деятельность. 8 класс
Предпринимательская деятельность. 8 класс Архетипы
Архетипы The semantic structure of word and its analysis
The semantic structure of word and its analysis Открытие рынков капитала для российского транспортного сектора
Открытие рынков капитала для российского транспортного сектора Методы тренировки мышц кистей и предплечий в гиревом спорте
Методы тренировки мышц кистей и предплечий в гиревом спорте Презентация на тему Новелла
Презентация на тему Новелла Modern technologies in Express Publishing course books
Modern technologies in Express Publishing course books CERT AM servicesСервисы CERT AM
CERT AM servicesСервисы CERT AM Естественно-научная и гуманитарная культуры
Естественно-научная и гуманитарная культуры Вклад отечественных ученых в разработку учения о высшей нервной деятельности
Вклад отечественных ученых в разработку учения о высшей нервной деятельности Автомеханик
Автомеханик Определение права, размера и сроков назначения трудовых пенсий
Определение права, размера и сроков назначения трудовых пенсий ГК «Роснанотех»: Итоги деятельности и перспективы развития
ГК «Роснанотех»: Итоги деятельности и перспективы развития TestWorks
TestWorks Священство. Таинства церкви
Священство. Таинства церкви Презентация на тему Степи. Растительность степи
Презентация на тему Степи. Растительность степи Теория и практика ценовой дискриминации
Теория и практика ценовой дискриминации