Содержание
- 2. Площадь- это.. Квадратный сантиметр- это площадь квадрата со стороной 1 см.. Что бы найти площадь фигуры
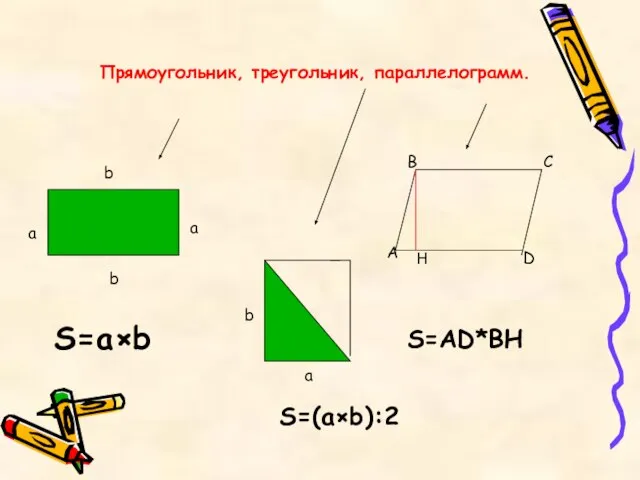
- 3. Прямоугольник, треугольник, параллелограмм. а b D A B C b a S=a×b S=AD*BH b a S=(a×b):2
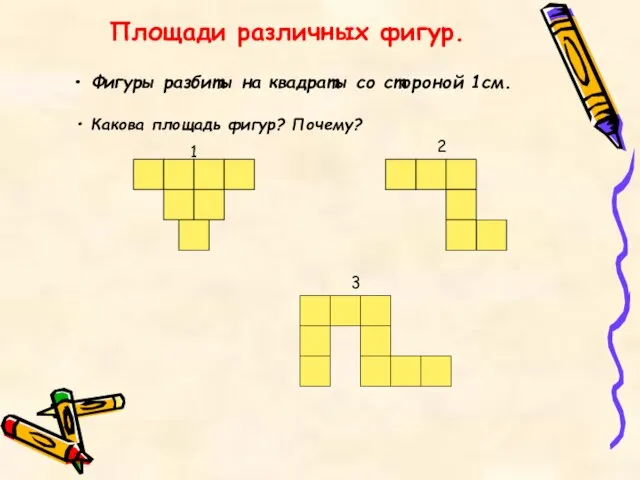
- 4. Площади различных фигур. 1 2 3 Фигуры разбиты на квадраты со стороной 1см. Какова площадь фигур?
- 5. Единицы измерения площадей. Квадратный миллиметр. Квадратный сантиметр. Гектар.(1га=10 000м²) Ар.(1а=100м²)
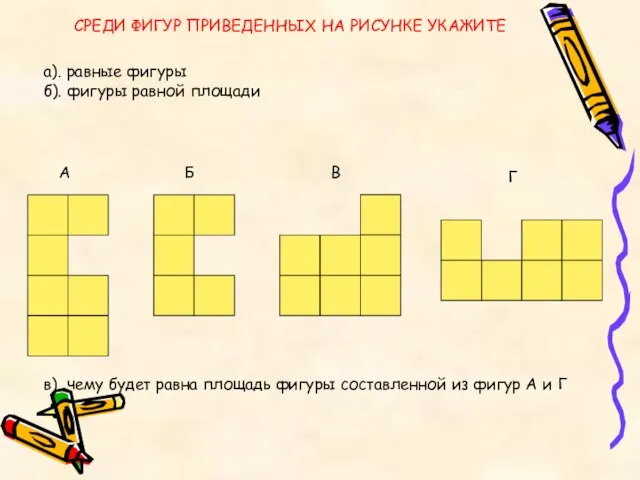
- 6. СРЕДИ ФИГУР ПРИВЕДЕННЫХ НА РИСУНКЕ УКАЖИТЕ а). равные фигуры б). фигуры равной площади в). чему будет
- 7. Решите ребус П ``` `` `````` ь
- 8. ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА РАВНА ПРОИЗВЕДЕНИЮ ЕГО СМЕЖНЫХ СТОРОН Дано: Доказать: ABCD-прямоугольник S=ab AB=b AD=a SABCD=S Доказательство: 1)
- 9. Площадь параллелограмма Дано: ABCD-параллелограмм Доказать: S=AD*BH Доказательство: трапеция ABCK составлена из параллелограмма и треугольника DCK. С
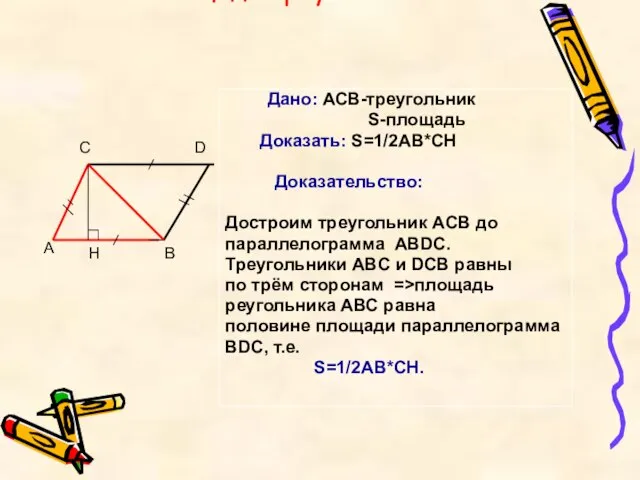
- 10. Площадь треугольника Дано: АСВ-треугольник S-площадь Доказать: S=1/2AB*CH Доказательство: Достроим треугольник ACB до параллелограмма ABDC. Треугольники ABC
- 11. Теорема Пифагора. Дано: Прямоугольный треугольник a, b-катеты, c-гипотенуза Доказать: c2 = a2 + b2 Доказательство: Достроим
- 12. Литература Л.С.Атанасян, В.Ф.Бутузов и другие, Геометрия: учебник для 7-9 классов А.В.Погорелов, Геометрия: учебник для 7-11 классов
- 14. Скачать презентацию







 ВодорастворимыеРастительныеМасла (ВРМ)
ВодорастворимыеРастительныеМасла (ВРМ) Областные особенности русского костюма
Областные особенности русского костюма Проект на тему: Фэн-шуй ( | ) в классной комнате. - презентация
Проект на тему: Фэн-шуй ( | ) в классной комнате. - презентация Панели стеновые CPL
Панели стеновые CPL Подготовка к ЕГЭ. Решение задач на движение
Подготовка к ЕГЭ. Решение задач на движение Презентация замороженных фруктовых пюре и ягод Dira
Презентация замороженных фруктовых пюре и ягод Dira Зеленый наряд нашего города
Зеленый наряд нашего города Техника квиллинг
Техника квиллинг «Атлас флоры и фауны Белого моря» это коллективная монография, подготовленная большой группой специалистов. Книга дает возможнос
«Атлас флоры и фауны Белого моря» это коллективная монография, подготовленная большой группой специалистов. Книга дает возможнос Текхнология блокчейн: инвестиции в будущее
Текхнология блокчейн: инвестиции в будущее Выгода открытия бизнеса в 2020 году
Выгода открытия бизнеса в 2020 году Изменение фоновых картинок в презентациях PowerPoint и текстовом редакторе Word
Изменение фоновых картинок в презентациях PowerPoint и текстовом редакторе Word Романтизм в русской живописи XIX века
Романтизм в русской живописи XIX века Развитие методов синтеза, исследование физико-химических и электрофизических свойств модифицированных наноуглеродных и фторугл
Развитие методов синтеза, исследование физико-химических и электрофизических свойств модифицированных наноуглеродных и фторугл Профи-digest
Профи-digest lecture_5
lecture_5 Виды сказуемых
Виды сказуемых Radiographic Interpretation of Infections of Jaws
Radiographic Interpretation of Infections of Jaws phpm2fa0e_ovosibirskaya-oblast
phpm2fa0e_ovosibirskaya-oblast Итоги 2-й четверти
Итоги 2-й четверти Математика-царица наук?
Математика-царица наук? Экономический смысл налогообложения
Экономический смысл налогообложения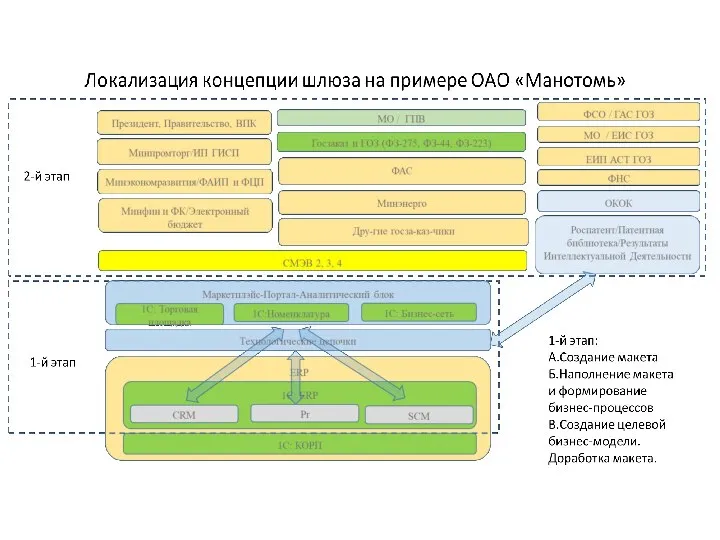 Локализация концепции шлюза на примере ОАО Манотомь
Локализация концепции шлюза на примере ОАО Манотомь Презентация на тему Справедливость и равенство
Презентация на тему Справедливость и равенство Protection of environment
Protection of environment Статусы пассажиров. Служебные пассажиры
Статусы пассажиров. Служебные пассажиры Буквы Ч и Щ в суффиксах имён существительных
Буквы Ч и Щ в суффиксах имён существительных Отдыхаем на отлично
Отдыхаем на отлично