ПЛОСКА СИСТЕМА ДОВІЛЬНО РОЗМІЩЕНИХ СИЛ

1. Приведення сили до точки
Будь - яку силу F, прикладену до тіла в точці А,
можна переносити паралельно лінії дії в будь-яку точку О,
приєднавши пару сил, момент якої рівний моменту
даної сили відносно нової точки її прикладання.
Рисунок 1
Рисунок 2
Рисунок 3

2. Приведення до точки плоскої системи
довільно розміщених сил
Довільна плоска система сил еквівалентна одній силі – рівнодійній системі і одній парі, момент якої рівний головному моменту.
Рівнодійна системи:
Головний момент системи:
Модуль головного вектора визначають за формулою:
Напрямок рівнодійної системи:

Рівнодійна довільної плоскої системи сил рівна головному вектору,
а відстань від центру приведення
до лінії дії рівнодійної
рівна відношенню головного моменту на модуль рівнодійної.
Приведення до точки плоскої системи
довільно розміщених сил

3. Теорема Варіньона
П'єр Варіньон (1654-1723) - французький математик і механік.
У 1725 році в Парижі було видано трактат Варіньона
«Нова механіка або статика», що представляє собою систематичний виклад вчення про складання і розкладанні сил, про моменти сил і правила оперування ними.
Цей виклад майже без змін зберігся в підручниках зі статики до нашого часу.
Момент рівнодійної довільної плоскої системи сил відносно будь-якої точки рівний алгебраїчній сумі моментів сил системи, взятих відносно тієї ж точки.
Цю рівність можна записати у вигляді:

4. Рівняння рівноваги і його різні форми
1.
2.
3.
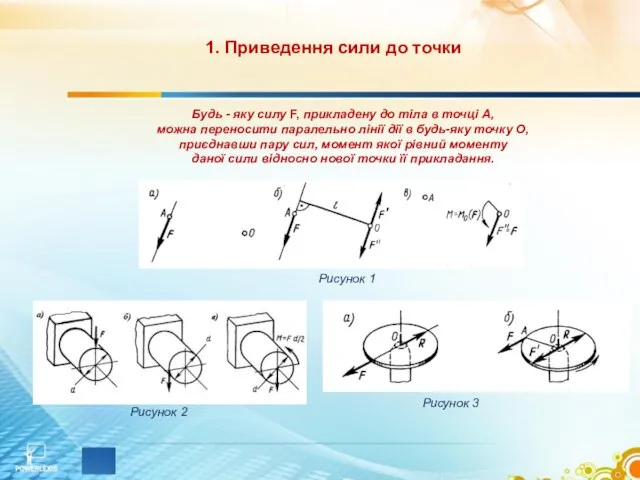
Для того, щоб тіло під дією плоскої системи довільно розміщених сил перебувало в рівновазі, необхідно і достатньо, щоб алгебраїчні суми проекцій усіх сил на дві взаємно перпендикулярні осі і моментів усіх сил відносно будь-якої точки в площині дії цих сил дорівнювали нулю.
Якщо довільна плоска система сил перебуває в рівновазі, то алгебраїчні суми моментів сил відносно двох будь-яких точок, а також проекцій сил на вісь, не перпендикулярну до прямої, яка проходить через ці точки, дорівнюють нулю.
Якщо довільна плоска система сил перебуває в рівновазі, то алгебраїчні суми моментів сил відносно будь-яких трьох точок, які не лежать на одній прямій, дорівнює нулю.

5. Балкові системи. Різновиди опор і види навантаження.

Різновиди опор і види навантаження.

Класифікація навантажень

6. Реальні в’язі. Тертя ковзання і його закони.
Реальні в’язі - в’язі з тертям
Ідеальні в’язі - в’язі без тертя

Тертя ковзання і його закони

Кут і конус тертя