отличница, но не спортсменка.
3. Существует треугольник, все углы которого тупые.
4. Сумма углов каждого треугольника равна 1800.
А) Все ученики нашего класса решили задачу.
В) В городе Томске есть сорокаэтажные здания.
С) Ни одно здание города Томска не имеет сорок этажей.
D) Существуют ученики в нашем классе, не решившие задачу.
E) Никто в нашем классе не решил задачу.
F) В городе Томске все здания сорокаэтажные.
[Ответ: (А, D),( В , С).]
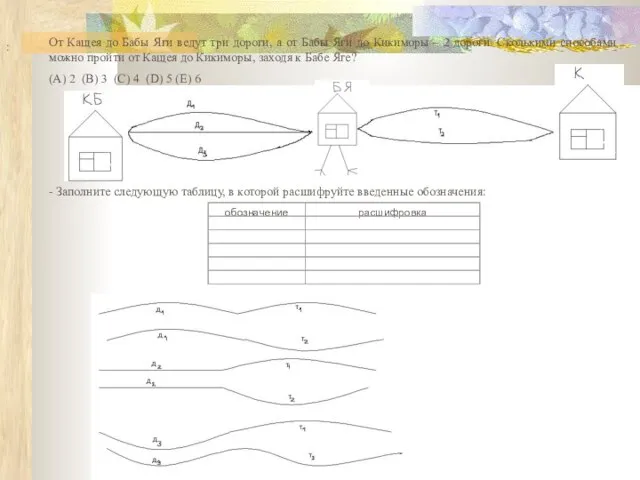
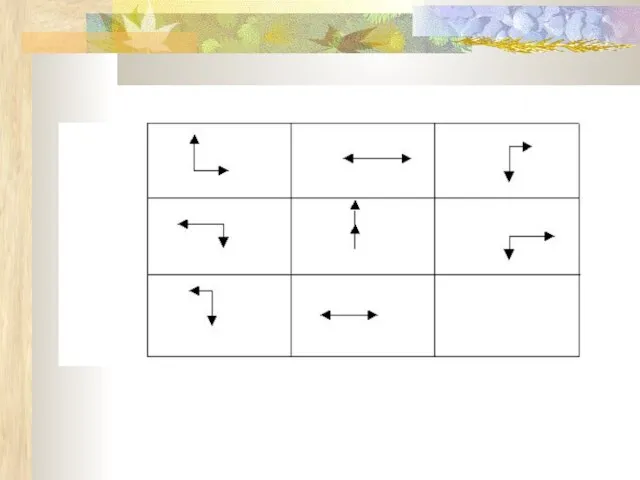
- Постройте по данной схеме отрицание следующих утверждений и в каждой паре определите, какое из них истинно.
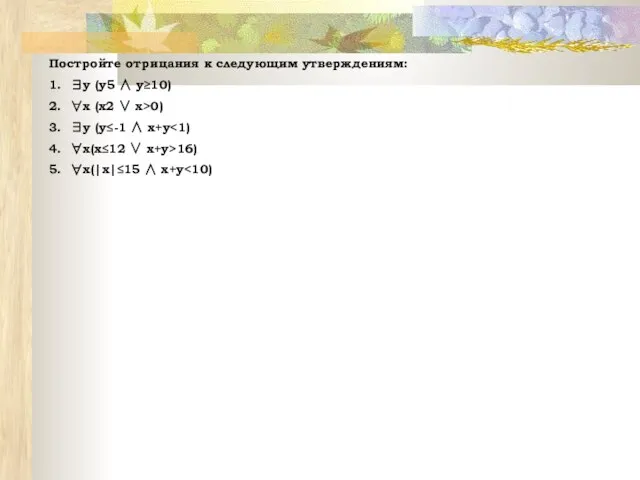
1. Все углы данного шестиугольника тупые.
2. Для каждого х из множества целых чисел выполняется неравенство х2>4.
3. Некоторые люди – дети.
4. По крайней мере для одного целого числа х имеет место х2-2х+1=0.
5. Все мужчины выше двух метров.
Все простые числа – четные
II.
III.
I.










 Маркетинговое планирование
Маркетинговое планирование Психологическая подготовка к всероссийской олимпиаде профессионального мастерства. 2021г
Психологическая подготовка к всероссийской олимпиаде профессионального мастерства. 2021г ЗНАЧЕНИЕ МИРОВОГО ОКЕАНА В ЖИЗНИ ЛЮДЕЙ
ЗНАЧЕНИЕ МИРОВОГО ОКЕАНА В ЖИЗНИ ЛЮДЕЙ Ночь искусств. Театр как вид искусства
Ночь искусств. Театр как вид искусства Герои Чернушки
Герои Чернушки Фотография авангарда
Фотография авангарда Здоровье – ни с чем не сравнимая ценность. 5 класс
Здоровье – ни с чем не сравнимая ценность. 5 класс На востоке встаёт луна, На западе гаснет солнце, А ветка вишни моей цветёт. Суворова Альбина 8 класс, школа 541
На востоке встаёт луна, На западе гаснет солнце, А ветка вишни моей цветёт. Суворова Альбина 8 класс, школа 541 Юные герои Первой мировой войны
Юные герои Первой мировой войны Методика проведения международных маркетинговых исследований Дисциплина: Международный маркетинг Преподаватель: профессор ка
Методика проведения международных маркетинговых исследований Дисциплина: Международный маркетинг Преподаватель: профессор ка Презентация на тему Скульптура Древнего Рима
Презентация на тему Скульптура Древнего Рима  Переобучение, повышение квалификации женщин, находящихся в отпуске по уходу за ребенком
Переобучение, повышение квалификации женщин, находящихся в отпуске по уходу за ребенком Международно-правовое регулирование охраны труда
Международно-правовое регулирование охраны труда Бандажна проходка
Бандажна проходка Дмитрий Иванович Мендилеев
Дмитрий Иванович Мендилеев Персоналии в отечественной социальной психологии
Персоналии в отечественной социальной психологии Презентация на тему Презентации Омар Хайям
Презентация на тему Презентации Омар Хайям Тепло из недр Земли
Тепло из недр Земли Успешный опыт использования поисковой интернет- рекламы в продажах садовой техники - ООО «Садторг» (www.dom-sad.ru, www.tehnosad.ru)www.dom-sad.ruwww.tehnos
Успешный опыт использования поисковой интернет- рекламы в продажах садовой техники - ООО «Садторг» (www.dom-sad.ru, www.tehnosad.ru)www.dom-sad.ruwww.tehnos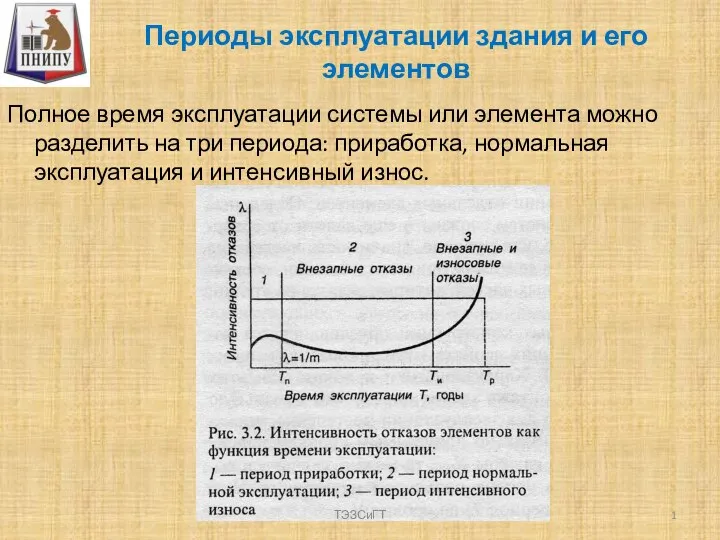 Периоды эксплуатации здания и его элементов
Периоды эксплуатации здания и его элементов Подборка телерекламы из Интернета по объекту рекламирования
Подборка телерекламы из Интернета по объекту рекламирования Когнитивные особенности младенца
Когнитивные особенности младенца Практика защиты авторских прав для произведений в интернете
Практика защиты авторских прав для произведений в интернете Презентация на тему Водные ресурсы мира (10 класс)
Презентация на тему Водные ресурсы мира (10 класс) Работа выполнена в рамках проекта «Повышение квалификаций различных категорий работников образования и формирование у них базов
Работа выполнена в рамках проекта «Повышение квалификаций различных категорий работников образования и формирование у них базов Компьютерный дизайн как профессия
Компьютерный дизайн как профессия БАСНИ- «КНИГА МУДРОСТИ САМОГО НАРОДА» (Н.В.ГОГОЛЬ)
БАСНИ- «КНИГА МУДРОСТИ САМОГО НАРОДА» (Н.В.ГОГОЛЬ) Производитель комплектующих для промышленной вентиляции
Производитель комплектующих для промышленной вентиляции