Погрешности преобразователей. Лекция 14

СТАТИЧЕСКАЯ ПЕРЕДАТОЧНАЯ ФУНКЦИЯ АЦП И ЦАП И
ПОГРЕШНОСТИ ПО ПОСТОЯННОМУ ТОКУ
Разрешающая способность АЦП или ЦАП может быть выражена несколькими различными способами: весом младшего разряда (LSB − Least Significant Bit, МЗР – младший значащий разряд), долей от полной шкалы размером в один миллион (ppm FS – part per million Full Scale – одна часть на миллион полной шкалы), милливольтами (мВ) и так далее.
Некоторые значения младшего значащего разряда (LSB) приведены в таблице 1.
Таблица 1. Квантование: значение младшего значащего бита (LSB)
*600 нВ - это тепловой шум в полосе частот 10кГц, возникающий на резисторе R=2.2 кОм при 25°C
Легко запомнить: 10-разрядное квантование при значении полной шкалы FS = 10,24В
соответствует LSB = 10,24 мВ,
точность 1000 ppm или 0.1%.
Все остальные значения можно вычислить умножением на
коэффициенты, равные степени числа 2.

На рисунке 1 представлена идеальная функция передачи однополярного 3-х разрядного ЦАП.
Рисунок 1 − Передаточная функция идеального 3-х разрядного ЦАП.
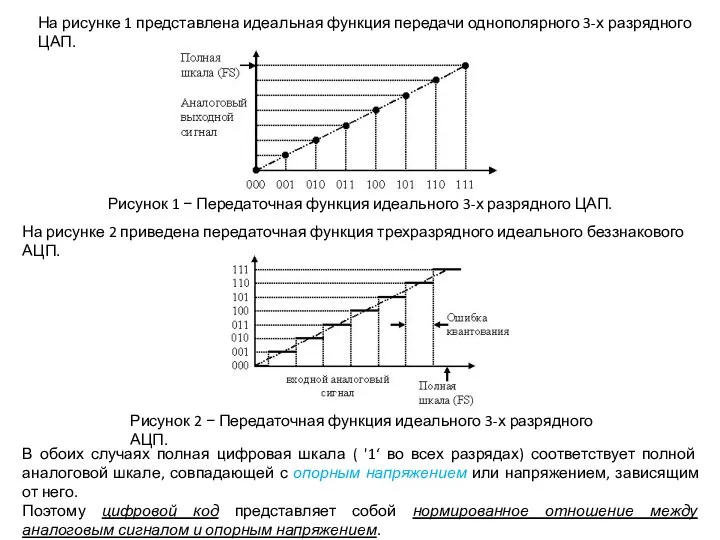
На рисунке 2 приведена передаточная функция трехразрядного идеального беззнакового АЦП.
Рисунок 2 − Передаточная функция идеального 3-х разрядного АЦП.
В обоих случаях полная цифровая шкала ( '1‘ во всех разрядах) соответствует полной аналоговой шкале, совпадающей с опорным напряжением или напряжением, зависящим от него.
Поэтому цифровой код представляет собой нормированное отношение между аналоговым сигналом и опорным напряжением.

Переход текущего выходного кода идеального АЦП к следующему цифровому коду происходит, начиная с напряжения, равного половине младшего разряда до напряжения, меньшего напряжения полной шкалы на половину младшего разряда.
Так как аналоговый сигнал на входе АЦП может принимать любое значение, а выходной цифровой сигнал является дискретным сигналом, то возникает ошибка между реальным входным аналоговым сигналом и соответствующим ему значением выходного цифрового сигнала.
Эта ошибка может достигать половины младшего разряда. Этот эффект известен как ошибка квантования или неопределенность преобразования. В устройствах, использующих сигналы переменного тока, эта ошибка квантования приводит к шуму квантования.
В настоящее время используются два типа биполярных АЦП:
— униполярный АЦП (более простой), на вход которого подается аналоговый сигнал с постоянной составляющей. Эта составляющая вводит смещение входного сигнала на величину, соответствующую единице старшего разряда (MSB). Во многих преобразователях можно переключать это напряжение или ток, для того чтобы использовать этот преобразователь как в режиме униполярного, так и в режиме биполярного преобразователя.
— знаковый АЦП (более сложный) и в нем кроме N информационных разрядов имеется дополнительный разряд, который показывает знак аналогового сигнала. Знаковые аналого-цифровые преобразователи применяются довольно редко, и используются в основном в составе цифровых вольтметров.

В АЦП и ЦАП различают четыре типа погрешностей:
две по постоянному току:
— погрешность смещения,
— погрешность усиления
и два типа погрешностей, связанных с линейностью.
— интегральная нелинейность и
— дифференциальная нелинейность.
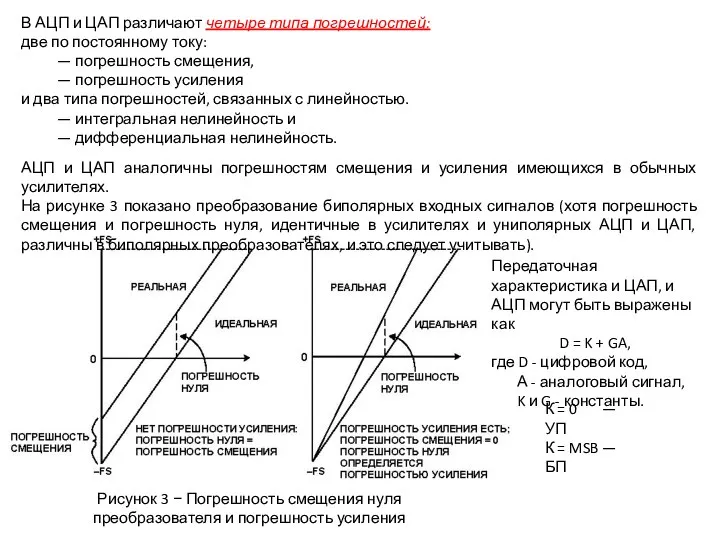
АЦП и ЦАП аналогичны погрешностям смещения и усиления имеющихся в обычных усилителях.
На рисунке 3 показано преобразование биполярных входных сигналов (хотя погрешность смещения и погрешность нуля, идентичные в усилителях и униполярных АЦП и ЦАП, различны в биполярных преобразователях, и это следует учитывать).
Рисунок 3 − Погрешность смещения нуля преобразователя и погрешность усиления
Передаточная характеристика и ЦАП, и АЦП могут быть выражены как
D = K + GA,
где D - цифровой код,
А - аналоговый сигнал,
K и G - константы.
К = 0 — УП
К = MSB — БП

Погрешность смещения преобразователя (аддитивная) — это величина, на которую фактическое значение коэффициента передачи K отличается от идеального значения. То есть это смещение всей передаточной характеристики влево или вправо относительно оси входного напряжения, как показано на рисуке 4 (в определение аддитивной погрешности АЦП намеренно включено смещение 1/2 LSB).
Рисунок 4 − Аддитивная погрешность
где Uвх.01 − значение входного напряжения, при котором происходит переход выходного кода из 0 в 1
Значения аддитивной погрешности указывается в милливольтах или в процентах от полной шкалы

Погрешность усиления — это величина, на которую коэффициент усиления G отличается от идеального значения.
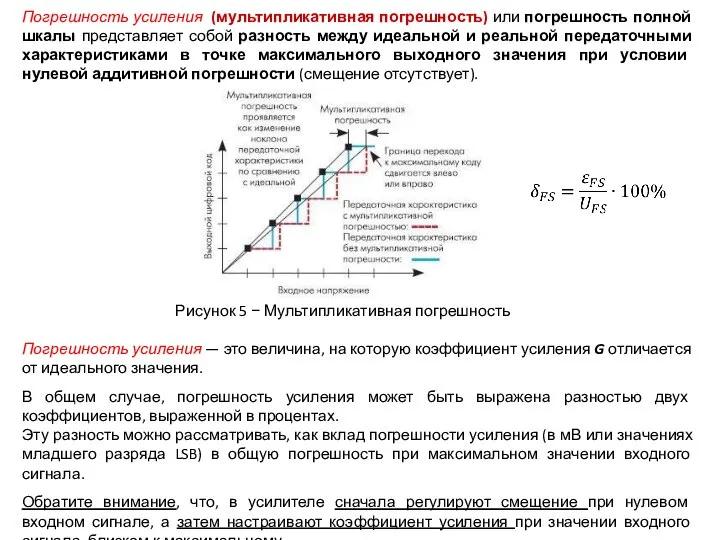
В общем случае, погрешность усиления может быть выражена разностью двух коэффициентов, выраженной в процентах.
Эту разность можно рассматривать, как вклад погрешности усиления (в мВ или значениях младшего разряда LSB) в общую погрешность при максимальном значении входного сигнала.
Обратите внимание, что, в усилителе сначала регулируют смещение при нулевом входном сигнале, а затем настраивают коэффициент усиления при значении входного сигнала, близком к максимальному.
Погрешность усиления (мультипликативная погрешность) или погрешность полной шкалы представляет собой разность между идеальной и реальной передаточными характеристиками в точке максимального выходного значения при условии нулевой аддитивной погрешности (смещение отсутствует).
Рисунок 5 − Мультипликативная погрешность

Интегральная нелинейность ЦАП и АЦП аналогична нелинейности усилителя и определяется как максимальное отклонение фактической характеристики передачи преобразователя от прямой линии.
В общем случае, она выражается в процентах от полной шкалы (но может представляться в значениях младших разрядов).
Существует два общих метода аппроксимации характеристики передачи:
— метод конечных точек (end point) (рисунок 6) и
— метод наилучшей прямой (best straight line) (рисунок 7).
Рисунок 6 − Метод измерения суммарной погрешности линейности – метод конечных точек
При использовании метода конечных точек измеряется отклонение произвольной точки характеристики (после коррекции усиления) от прямой, проведенной из начала координат. Таким образом в компании Analog Devices, Inc. измеряют значения интегральной нелинейности преобразователей, используемых в задачах измерения и управления (так как величина погрешности зависит от отклонения от идеальной характеристики, а не от произвольного "наилучшего приближения").

По методу наилучшего приближения через передаточную характеристику устройства проводят прямую линию, используя стандартные методы интерполяции кривой. После этого максимальное отклонение измеряется от построенной прямой.
Как правило, интегральная нелинейность, измеренная таким образом, учитывает только 50% нелинейности, оцененной методом конечных точек.
Метод наилучшей прямой дает более адекватный прогноз искажений в приложениях, имеющих дело с сигналами переменного тока. Он менее чувствителен к нелинейностям технических характеристик.
Это делает метод предпочтительным при указании впечатляющих технических характеристик в спецификации, но менее полезным для анализа реальных значений погрешностей.
Для приложений, имеющих дело с сигналами переменного тока, лучше определять гармонические искажения, чем нелинейность по постоянному току, так что для определения нелинейности преобразователя необходимость в использовании метода наилучшей прямой возникает довольно редко.
Рисунок 7 − Метод измерения суммарной погрешности линейности – метод наилучшей прямой

Другой тип нелинейности преобразователей — дифференциальная нелинейность (DNL).
DNL связана с нелинейностью кодовых переходов преобразователя (рисунок 8). В идеальном случае изменение на единицу младшего разряда цифрового кода точно соответствует изменению аналогового сигнала на величину единицы младшего разряда. В ЦАП изменение одного младшего разряда цифрового кода должно вызывать изменение сигнала на аналоговом выходе, в точности соответствующее величине младшего разряда. В то же время в АЦП при переходе с одного цифрового уровня на следующий значение сигнала на аналоговом входе должно измениться точно на величину, соответствующую младшему разряду цифровой шкалы.
Там, где изменение аналогового сигнала, соответствующее изменению единицы младшего разряда цифрового кода, больше или меньше этой величины, говорят об дифференциальной нелинейной (DNL) погрешности.
DNL-погрешность преобразователя обычно определяется как максимальное значение дифференциальной нелинейности, выявляемое на любом переходе.
Рисунок 8 − Метод определения дифференциальной нелинейности

Погрешность дифференциальной линейности определяет два важных свойства АЦП:
— монотонность характеристики преобразования и
— непропадание кодов.
Монотонность характеристики преобразования – возрастание (уменьшение) выходного напряжения ЦАП Uвых при возрастании (уменьшении) входного кода.
Если дифференциальная нелинейность больше относительного шага квантования h/UFS, то характеристика преобразователя немонотонна.
Непропадание кодов – свойство АЦП выдавать все возможные выходные коды при изменении входного напряжения от начальной до конечной точки диапазона преобразования.
При нормировании непропадания кодов указывается эквивалентная разрядность АЦП – максимальное количество разрядов АЦП, для которых не пропадают соответствующие им кодовые комбинации.

Если дифференциальная нелинейность ЦАП меньше, чем –1 LSB на любом переходе (рисунок 9), ЦАП называют немонотонным, и его характеристика передачи содержит один или несколько локальных максимумов или минимумов.
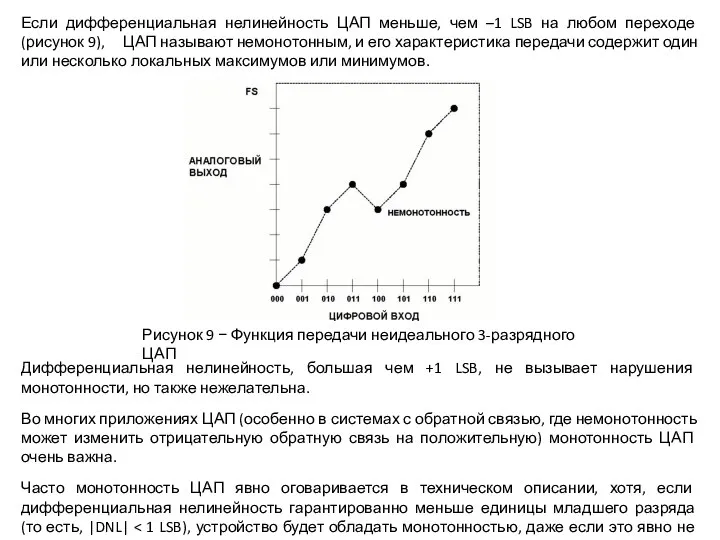
Дифференциальная нелинейность, большая чем +1 LSB, не вызывает нарушения монотонности, но также нежелательна.
Во многих приложениях ЦАП (особенно в системах с обратной связью, где немонотонность может изменить отрицательную обратную связь на положительную) монотонность ЦАП очень важна.
Часто монотонность ЦАП явно оговаривается в техническом описании, хотя, если дифференциальная нелинейность гарантированно меньше единицы младшего разряда (то есть, |DNL| < 1 LSB), устройство будет обладать монотонностью, даже если это явно не указывается.
Рисунок 9 − Функция передачи неидеального 3-разрядного ЦАП

Определение отсутствующих кодов (непропадание) сложнее, чем определение немонотонности.
Все АЦП характеризуются некоторым шумом перехода (transition noise), иллюстрируемым на рисунке 10 (этот шум можно представить как мелькание последней цифры цифрового вольтметра между соседними значениями).
По мере роста разрешающей способности диапазон входного сигнала, соответствующий уровню шума перехода, может достичь или даже превысить значение сигнала, соответствующее единице младшего разряда. В таком случае, особенно в сочетании с отрицательной DNL-погрешностью, может случиться так, что появятся некоторые (или даже все) коды, где шум перехода будет присутствовать во всем диапазоне значений входных сигналов.
Таким образом, возможно существование некоторых кодов, для которых не существует значения входного сигнала, при котором этот код гарантированно бы появился на выходе, хотя и может существовать некоторый диапазон входного сигнала, при котором иногда будет появляться этот код.
Температурная нестабильность − характеризуется температурными коэффициентами погрешности полной шкалы и погрешности смещения нуля.
Погрешности полной шкалы и смещения нуля могут быть устранены калибровкой (подстройкой).
Погрешности нелинейности простыми средствами устранить нельзя.
Рисунок 10 − Совместное действие шумов перехода кода и дифференциальной нелинейности

Рисунок 11 − Частотный спектр измеряемого сигнала. БПФ над выходными данными АЦП.
Нулевая гармоника (рисунок 11) соответствует основной частоте входного сигнала. Всё остальное представляет собой шум, который содержит гармонические искажения, тепловой шум, шум 1/f и шум квантования.
Некоторые составляющие шума генерируются самим АЦП, некоторые могут поступать на вход АЦП из внешних цепей.
Гармонические искажения, например, могут содержаться в измеряемом сигнале и одновременно генерироваться АЦП в процессе преобразования.
Динамические характеристики
Динамические характеристики АЦП обычно определяют с помощью методов спектрального анализа, например, по результатам выполнения быстрого преобразования Фурье (БПФ) над массивом выходных значений АЦП, соответствующих некоторому тестовому входному сигналу.

Шум квантования — это ошибка, возникающая при оцифровке аналогового сигнала. В зависимости от типа АЦП эта ошибка может возникать из-за округления (до определённого разряда) сигнала или усечения (отбрасывания младших разрядов) сигнала.
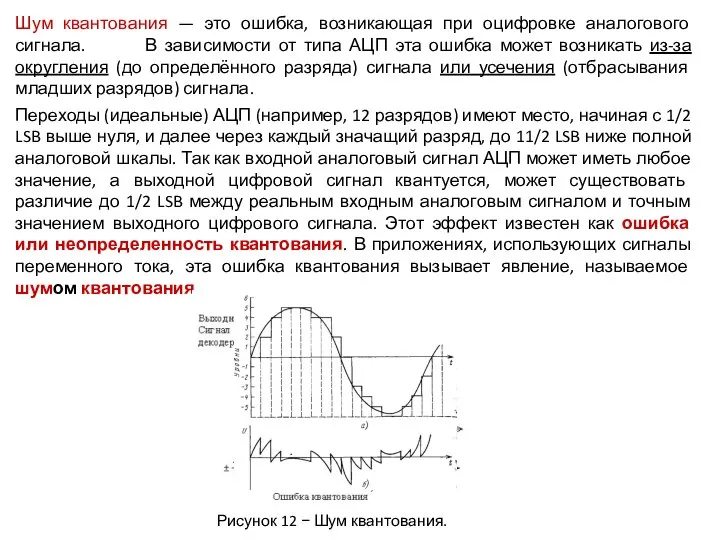
Переходы (идеальные) АЦП (например, 12 разрядов) имеют место, начиная с 1/2 LSB выше нуля, и далее через каждый значащий разряд, до 11/2 LSB ниже полной аналоговой шкалы. Так как входной аналоговый сигнал АЦП может иметь любое значение, а выходной цифровой сигнал квантуется, может существовать различие до 1/2 LSB между реальным входным аналоговым сигналом и точным значением выходного цифрового сигнала. Этот эффект известен как ошибка или неопределенность квантования. В приложениях, использующих сигналы переменного тока, эта ошибка квантования вызывает явление, называемое шумом квантования.
Рисунок 12 − Шум квантования.

Отношение "сигнал/шум"
Отношение "сигнал/шум" (SNR) – это отношение среднеквадратического значения величины входного сигнала к среднеквадратическому значению величины шума (за исключением гармонических искажений), выраженное в децибелах:
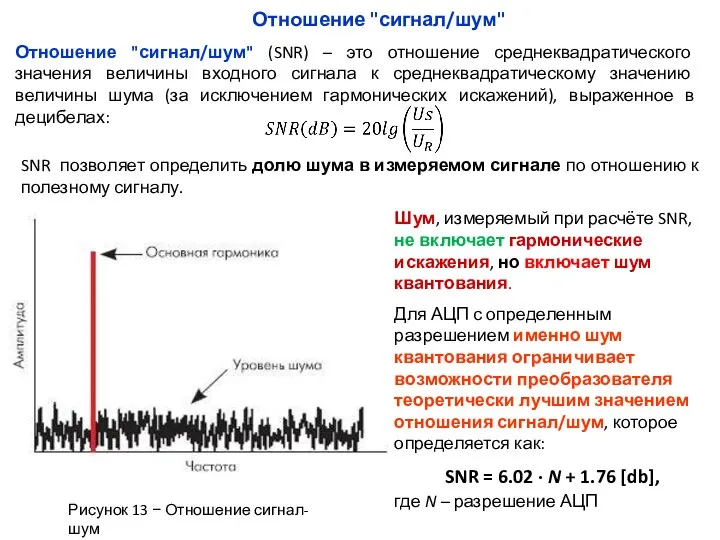
Рисунок 13 − Отношение сигнал-шум
Шум, измеряемый при расчёте SNR, не включает гармонические искажения, но включает шум квантования.
Для АЦП с определенным разрешением именно шум квантования ограничивает возможности преобразователя теоретически лучшим значением отношения сигнал/шум, которое определяется как:
SNR = 6.02 · N + 1.76 [db],
где N – разрешение АЦП
SNR позволяет определить долю шума в измеряемом сигнале по отношению к полезному сигналу.

Спектр шума квантования АЦП стандартных архитектур имеет равномерное распределение по частоте. Поэтому величина этого шума не может быть уменьшена путем увеличения времени преобразования и последующего усреднения результатов.
Шум квантования может быть снижен только путем проведения измерений с помощью АЦП большей разрядности.
Рисунок 14 − БПФ отражает гармонические искажения
Особенность сигма-дельта АЦП состоит в том, что спектр шума квантования у него распределен по частоте неравномерно − он смещен в сторону высоких частот.
Поэтому, увеличивая время измерения (и, соответственно, количество выборок измеряемого сигнала), накапливая и затем усредняя полученную выборку (фильтр нижних частот), можно получить результат измерений с более высокой точностью. Естественно, при этом общее время преобразования будет возрастать.