Показательная функция, ее свойства и график

Свойства показательной функции:
Функцию вида y=ax, где а>0, a≠1, х – любое число, называют показательной функцией.
Область определения показательной функции: D (y)=R – множество всех действительных чисел.
Область значений показательной функции: E (y)=R+ - множество всех положительных чисел.
Показательная функция y=ax возрастает при a>1.
Показательная функция y=ax убывает при 0

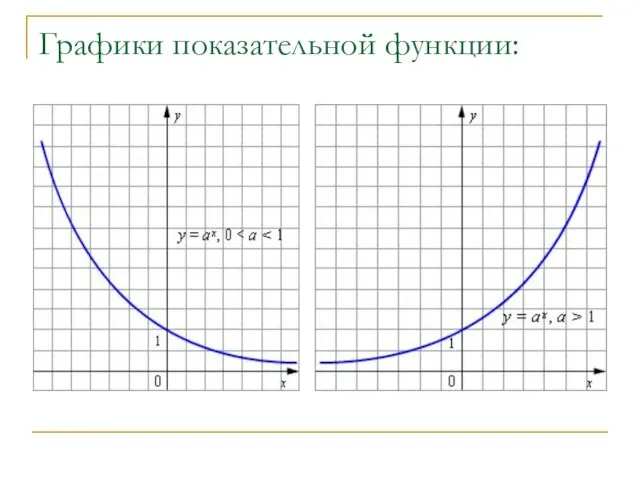
Графики показательной функции:

К общим свойствам показательной функции как при 0 < a < 1, так и при a > 1 относятся:

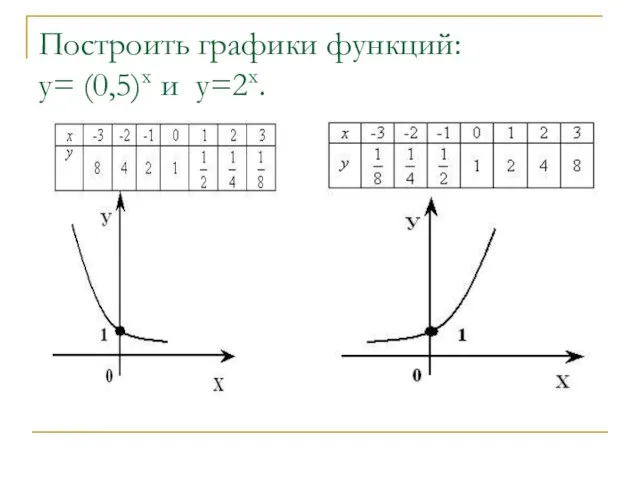
Построить графики функций:
у= (0,5)х и у=2х.

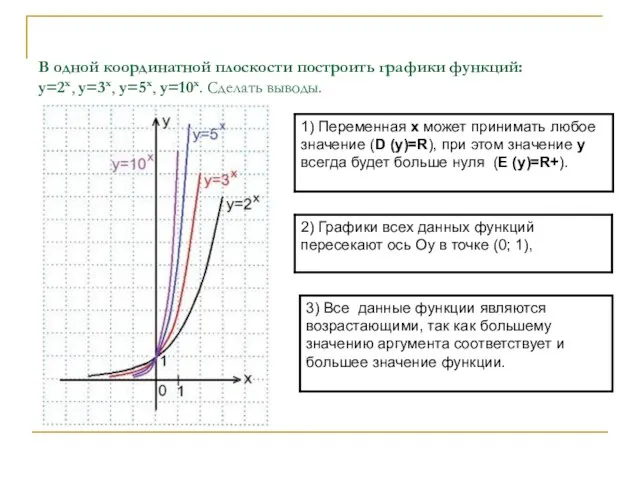
В одной координатной плоскости построить графики функций:
y=2x, y=3x, y=5x, y=10x. Сделать выводы.

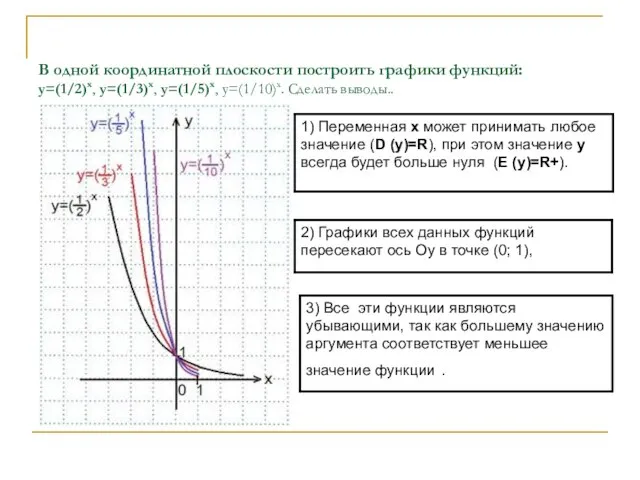
В одной координатной плоскости построить графики функций:
y=(1/2)x, y=(1/3)x, y=(1/5)x, y=(1/10)x. Сделать выводы..

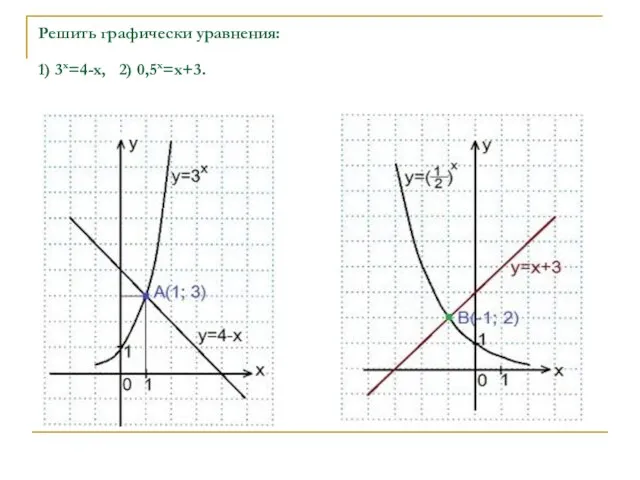
Решить графически уравнения:
1) 3x=4-x, 2) 0,5х=х+3.

Найти область значений функции: 1) y=-2x; 2) y=(1/3)x+1; 3) y=3x+1-5.