Содержание
- 2. Поле скорости по заданному полю вихрей и расхождения скорости
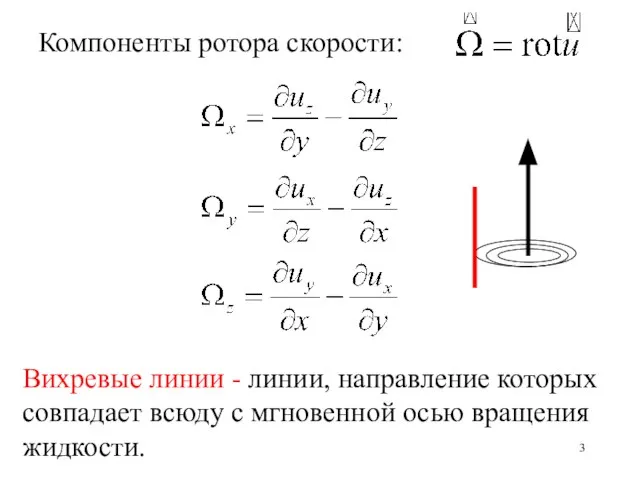
- 3. Компоненты ротора скорости: Вихревые линии - линии, направление которых совпадает всюду с мгновенной осью вращения жидкости.
- 4. Дифференциальное уравнение вихревых линий Если через каждую точку малой замкнутой кривой провести соответствующую вихревую линию, то
- 5. Задача Заданы распределения вихря и дивергенции скорости в любой точке жидкости, нормальная составляющая скорости на поверхности,
- 6. Предположения Жидкость заполняет все пространство, находится в покое на бесконечности. Заданы вихрь скорости Ω расхождение (дивергенция)
- 7. 5. На поверхностях разрыва нормальная составляющая Ω остается непрерывной Искомую скорость u будем рассматривать как сумму
- 8. Скорость задается уравнениями: существует
- 9. Для определения u1 получаем уравнение Пуассона Предположим, что функция Θ равна 0 всюду, кроме очень малой
- 10. По теореме Гаусса Т.е. объемный интеграл от расхождения вектора скорости равен потоку вектора скорости через поверхность
- 11. Пусть τ→0. Получаем картину течения от точечного источника в начале координат интенсивности 1. В силу симметрии
- 12. φ – функция только r, в сферических координатах нет зависимости от широты и долготы. Интегрируем:
- 13. Произвольная постоянная определяется из условия, что поток скорости через произвольную сферу с центром в начале координат
- 14. Получаем: Произвольная постоянная не влияет на величину скорости течения и может быть отброшена
- 15. Предположим, что интенсивность источника имеет значение q В этом случае
- 16. Если задано распределение источников Θ(ξ, η, ζ) Где r расстояние от точки N(x,y,z), где ищем поле
- 17. Решение системы
- 18. Определим вектор u2 для системы Удовлетворим второму уравнению, если положим где А – векторный потенциал. Тогда
- 19. Получаем уравнение: (Можно считать не нарушая общности)
- 21. Одна вихревая нить Несжимаемая жидкость, покоящаяся на бесконечности
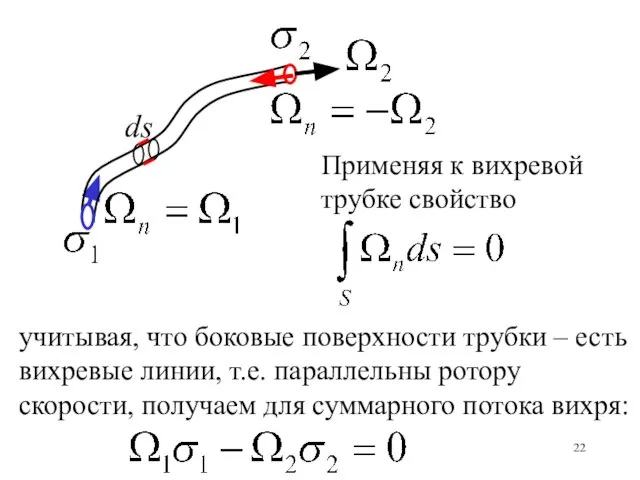
- 22. Применяя к вихревой трубке свойство учитывая, что боковые поверхности трубки – есть вихревые линии, т.е. параллельны
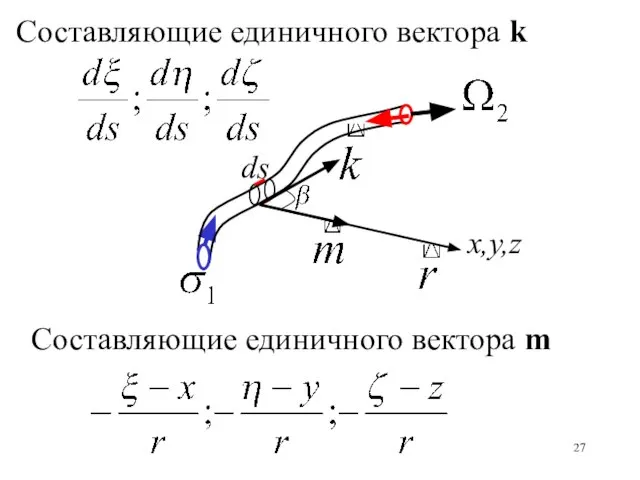
- 27. ds x,y,z Составляющие единичного вектора k Составляющие единичного вектора m
- 28. Вклад в величину скорости в точке (x,y,z) от элемента вихревой трубки ds определяется выражением:
- 29. Электродинамика: Сила, действующая на магнитный полюс в точке (x,y,z) от элемента проводника ds, по которому течет
- 30. Прямолинейные вихри плоское движение несжимаемая жидкость
- 31. Пусть движение происходит в плоскости х, у. Вихревые линии являются прямыми, параллельными оси z. ξ, η,
- 32. Скорость жидкости в точке (х, у) определяется: Считая ξ, η, (х, у, z) постоянными, интегрируем
- 33. Достаточно рассматривать движение на плоскости 0xy, причем вместо вихревой нити точку пересечения ее с плоскостью 0xy.
- 34. Найти комплексный потенциал для точечного вихря.
- 36. 2 вихря Две параллельные прямые вихревые нити в точках z1 и z2. Показать, что нити всегда
- 37. Комплексная сопряженная скорость
- 38. Скорость первого вихря в точке z1 (сам на себя не действует) Скорость второго вихря в точке
- 39. +
- 40. Получаем интеграл движения центра инерции системы двух вихрей Точка С (центр инерции) с координатами Остается неподвижной
- 41. Вычитаем из первого третье уравнение, из второго – четвертое.
- 42. Интегрируем и получаем: Расстояние между вихрями не меняется в процессе перемещения
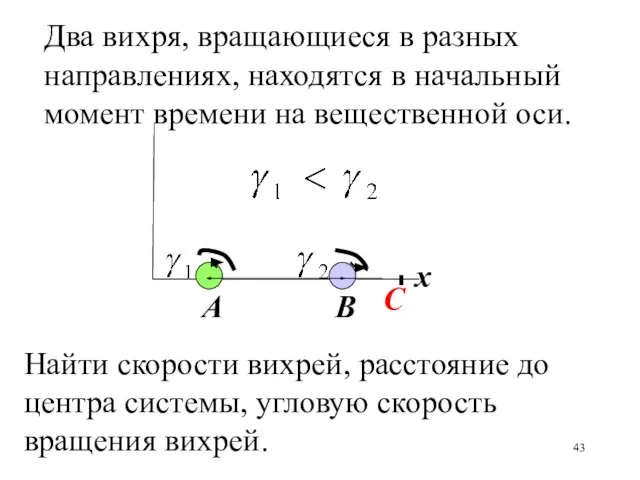
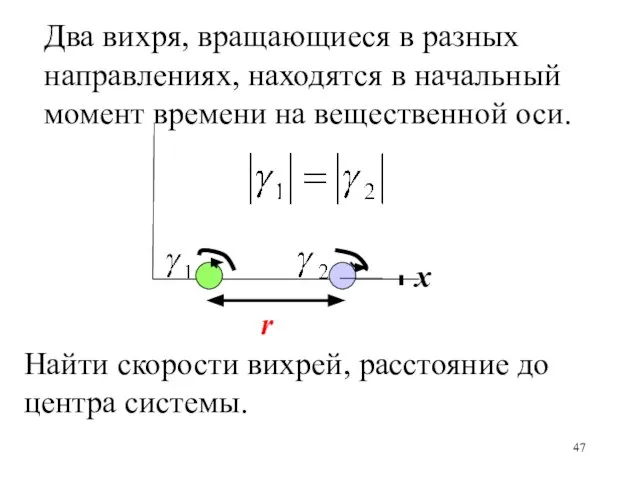
- 43. A B x С Два вихря, вращающиеся в разных направлениях, находятся в начальный момент времени на
- 44. Вихревая нить с координатами и циркуляцией γ сообщает жидкости в точке (х, у) скорость, компоненты которой
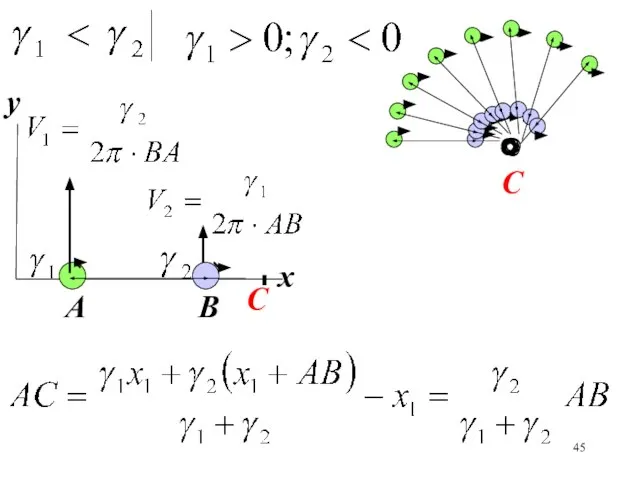
- 45. A B x y С С
- 46. Угловая скорость вращения вихрей вокруг центра С Где будет точка С, если вихри вращаются в одном
- 47. x r Два вихря, вращающиеся в разных направлениях, находятся в начальный момент времени на вещественной оси.
- 48. Скорость первого вихря в точке z1 (сам на себя не действует) Скорость второго вихря в точке
- 49. Отделяем вещественную часть от мнимой : Вихри перемещаются с постоянной скоростью, перпендикулярно прямой, соединяющей вихри в
- 50. Пример 1 Одна вихревая нить в точке (х,у), циркуляция скорости внутри бесконечно малого сечения имеет постоянное
- 51. х у r Центр одиночного вихря не смещается во времени.
- 52. Пример 2 Внутри круга радиуса а жидкость вращается как твердое тело с угловой скоростью ω. Определить
- 53. х у r На границе вихря скорость равна ω a. а
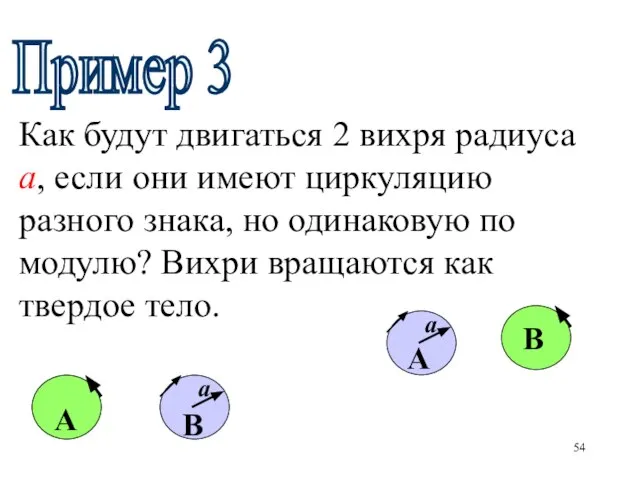
- 54. Как будут двигаться 2 вихря радиуса а, если они имеют циркуляцию разного знака, но одинаковую по
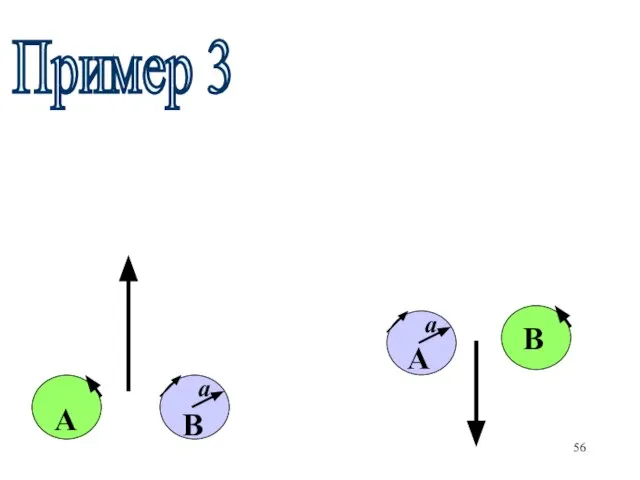
- 55. Движение двух вихрей с противоположным направлением вращения и С А АС=∞ V1=V2= Вихри двигаются по прямой
- 56. Пример 3 А а В а А В
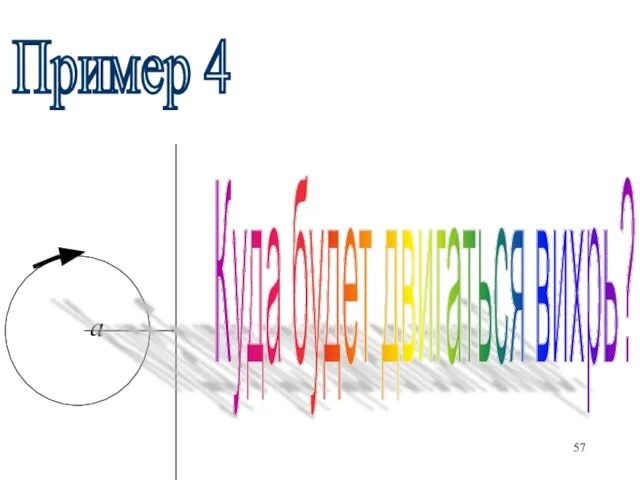
- 57. а Куда будет двигаться вихрь? Пример 4
- 58. Найти скорость перемещения вихря у твердой стенки
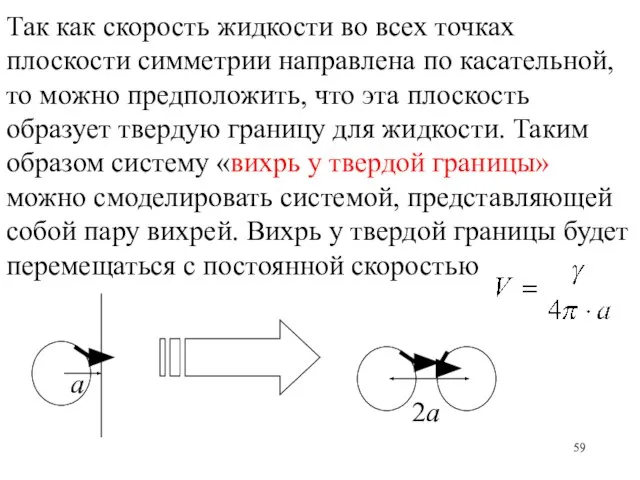
- 59. Так как скорость жидкости во всех точках плоскости симметрии направлена по касательной, то можно предположить, что
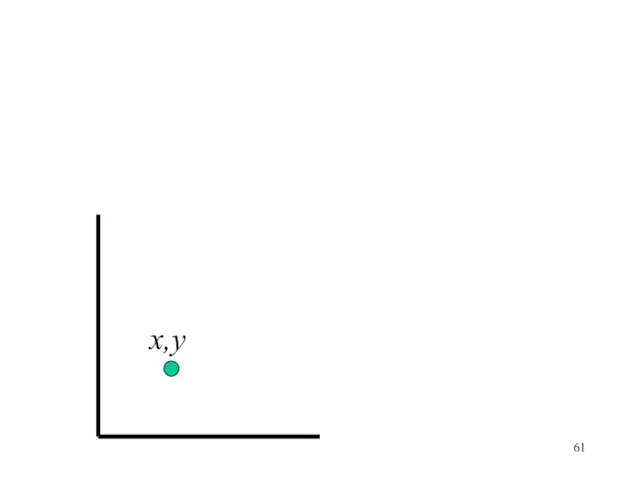
- 60. Пример 5 В точке с координатами х,у находится прямая вихревая нить. Жидкость ограничена твердыми стенками, образующими
- 61. x,y
- 62. Так как циркуляция скорости вихря постоянна, то течение стационарно. В этом случае траектория вихря совпадает с
- 63. x,y -x,y
- 64. Для того, чтобы описать влияние стенки, расположенной вдоль действительной оси, поместим вихри той же интенсивности, но
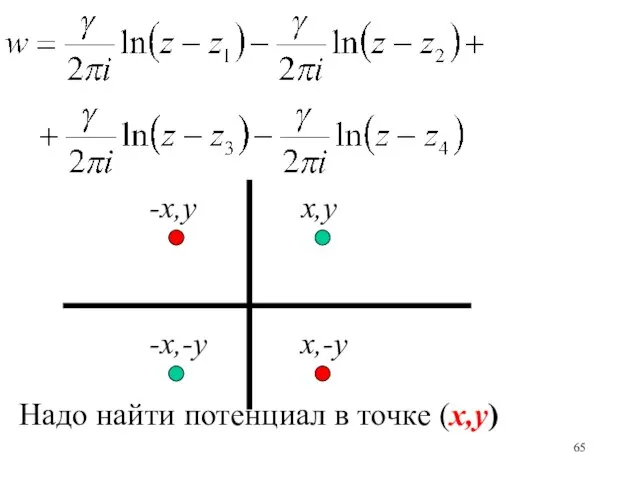
- 65. x,y -x,y x,-y -x,-y Надо найти потенциал в точке (x,y)
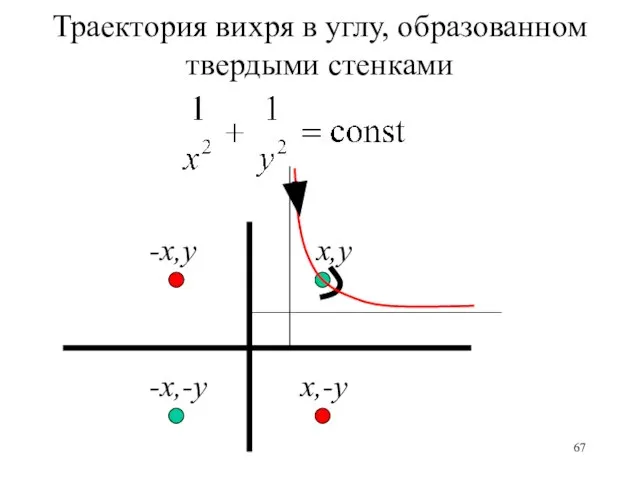
- 66. На линии тока ψ=const, т.е.
- 67. x,y -x,y x,-y -x,-y Траектория вихря в углу, образованном твердыми стенками
- 78. расположенных в точках z1,…, zn и имеющих интенсивности γ1, …, γn Комплексный потенциал Комплексная скорость Записать
- 79. Уравнение движения вихря в точке zp (k=p) Умножая на γp и суммируя по переменной p от
- 80. Следовательно Получаем Отделяем мнимую и действительную части
- 81. Если , то получаем интегралы движения центров инерции (следствие 1)
- 82. Следствие 2 Уравнение движения вихря в точке zp (k=p) Умножая на γp zp и суммируя по
- 83. Сумма моментов количеств движения масс γp относительно начала координат не меняется со временем (1) (2) (2)
- 84. (1)
- 85. Сумма моментов инерции масс γp относительно начала координат не меняется со временем
- 86. Умножая выражения скорости на и суммируя по переменной p от 1 до n, получаем еще один
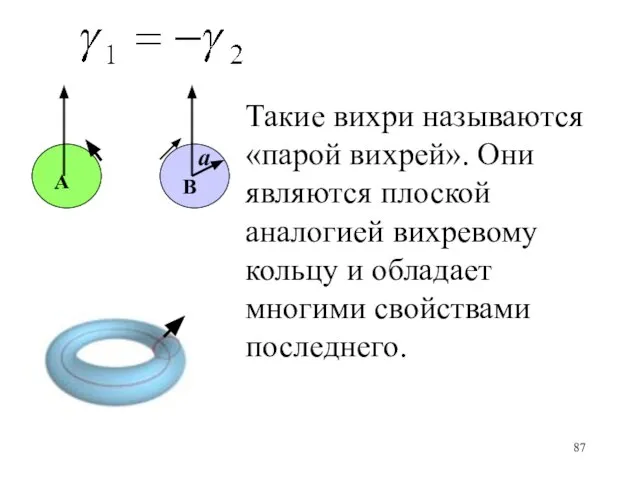
- 87. А а В Такие вихри называются «парой вихрей». Они являются плоской аналогией вихревому кольцу и обладает
- 88. Куда двигается кольцевой вихрь?
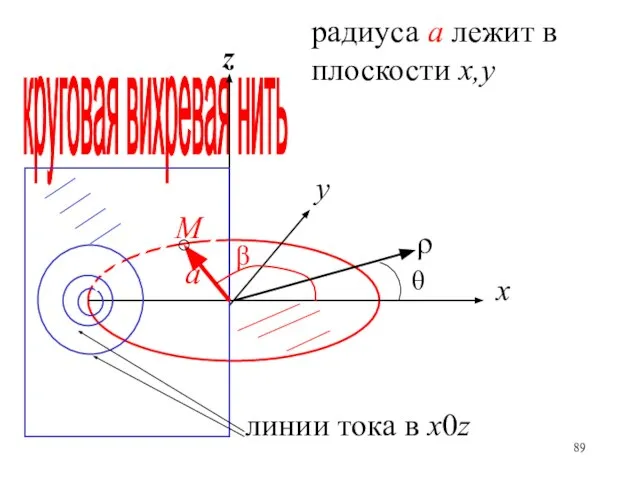
- 89. круговая вихревая нить радиуса а лежит в плоскости х,у
- 90. Координаты точки М на вихревой нити в декартовой системе (x, y, z) Расстояние от точки М
- 91. (1) Запишем компоненты скорости через векторный потенциал
- 93. Для векторного потенциала в точке x,y,z
- 94. Для плоскости x,y при θ=0 Вследствие симметрии задачи это справедливо для всех углов θ
- 96. Подставляем выражения векторного потенциала в (1) и находим компоненты скорости
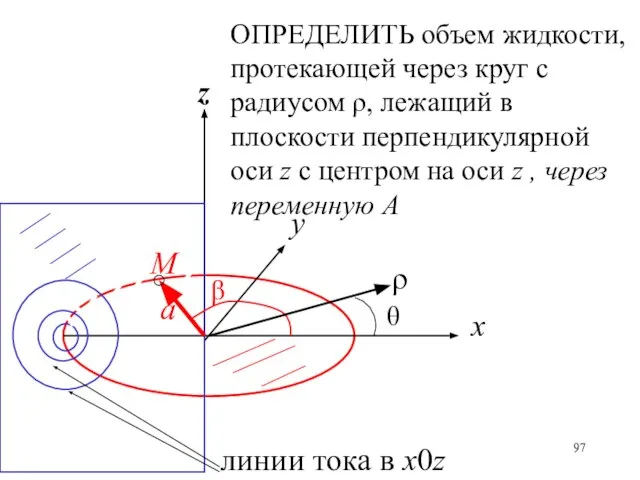
- 97. ОПРЕДЕЛИТЬ объем жидкости, протекающей через круг с радиусом ρ, лежащий в плоскости перпендикулярной оси z с
- 98. Объем жидкости, протекающей через круг с радиусом ρ, лежащим в плоскости перпендикулярной оси z с центром
- 99. ОПРЕДЕЛИТЬ скорость перемещения круговой вихревой нити
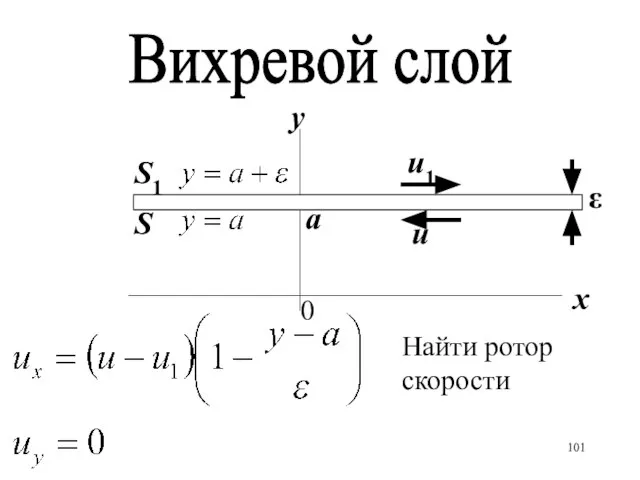
- 101. Вихревой слой 0 а S S1 x y ε u1 u Найти ротор скорости
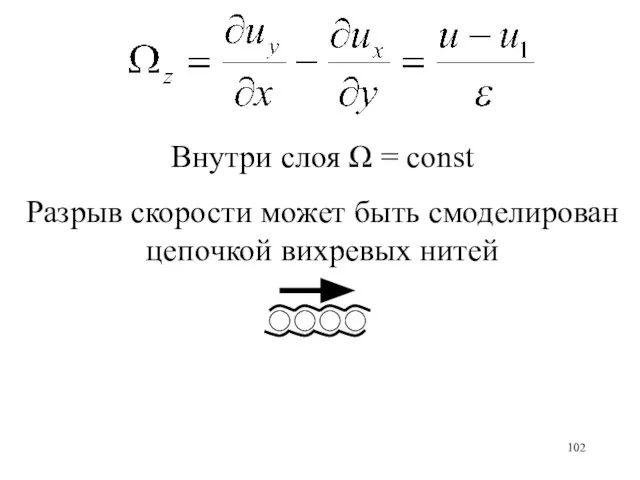
- 102. Внутри слоя Ω = const Разрыв скорости может быть смоделирован цепочкой вихревых нитей
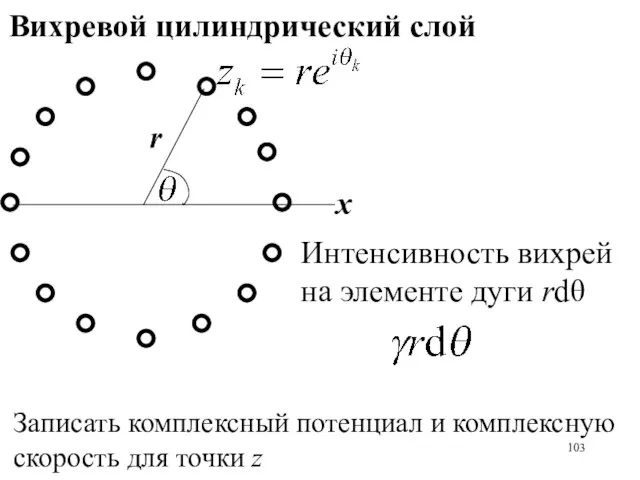
- 103. Вихревой цилиндрический слой x r Интенсивность вихрей на элементе дуги rdθ Записать комплексный потенциал и комплексную
- 104. Комплексный потенциал цилиндрического слоя в точке z Комплексная скорость Делим подинтегральное выражение на z, умножаем на
- 105. z рассматривается как постоянная при интегрировании
- 106. Если z внутри окружности, т.е. При изменении θ от 0 до 2π аргумент разности меняется на
- 107. Если z вне окружности, т.е. При изменении θ от 0 до 2π конец вектора обходит замкнутый
- 108. Комплексная скорость движения нет внутри цилиндра вне цилиндра движение описывается воздействием вихревой нити интенсивности 2πrγ, расположенной
- 109. 2 3 КОНТРОЛЬНАЯ РАБОТА
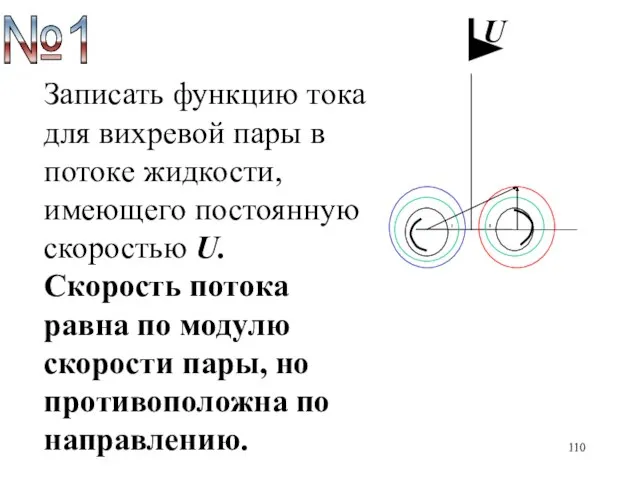
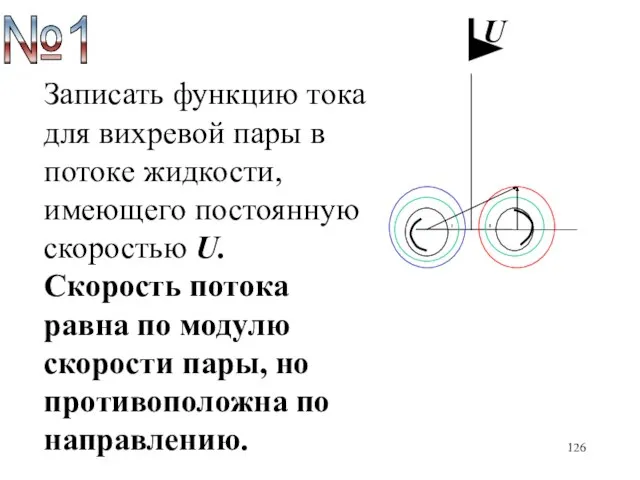
- 110. U Записать функцию тока для вихревой пары в потоке жидкости, имеющего постоянную скоростью U. Скорость потока
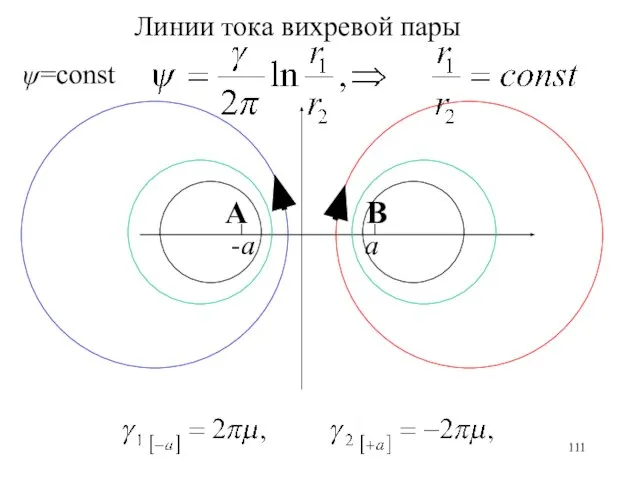
- 111. ψ=const Линии тока вихревой пары А В
- 112. Функция тока для течения, имеющего постоянную скорость вдоль оси ординат
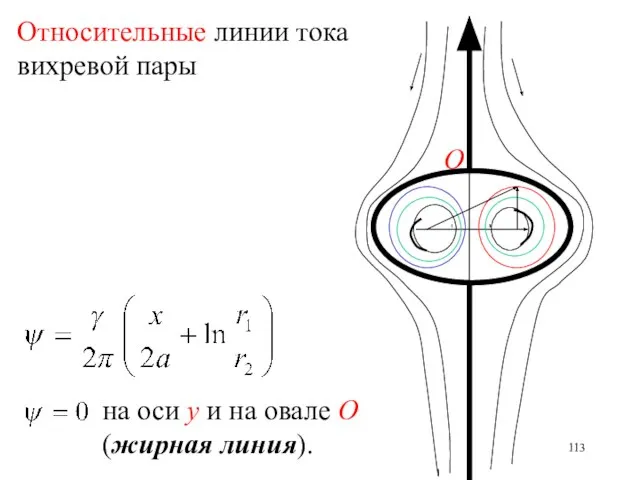
- 113. Относительные линии тока вихревой пары О на оси у и на овале О (жирная линия).
- 114. Жидкость внутри овала О движется вместе с вихрями. Жидкость вне овала О обтекает этот овал как
- 115. Найти в ортогональной системе координат уравнения линий тока для 1) случая двух вихрей одинаковой интенсивности 2)
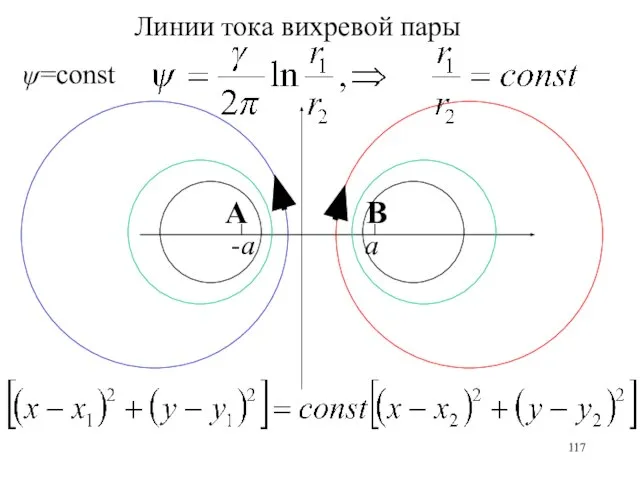
- 116. На линии тока z2 z1
- 117. ψ=const Линии тока вихревой пары А В
- 118. №3
- 119. При обтекании цилиндра жидкостью, его поверхность должна быть линией тока, а ψ=const. Пусть в центре цилиндра
- 120. При обтекании цилиндра жидкостью, его поверхность должна быть линией тока, а ψ=const. Пусть в центре цилиндра
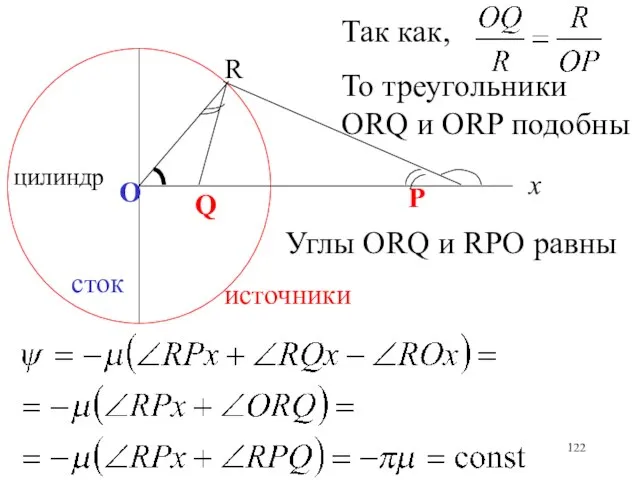
- 122. х цилиндр Р О Q R источники сток Так как, То треугольники ORQ и ORP подобны
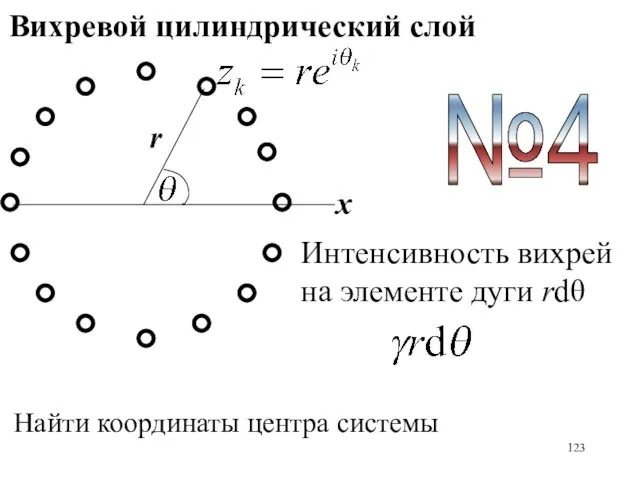
- 123. Вихревой цилиндрический слой x r Интенсивность вихрей на элементе дуги rdθ Найти координаты центра системы №4
- 124. Интенсивность твердотельно вращающихся вихрей такова, что тангенциальные составляющие скорости в точках соприкосновения равны Найти координаты центра
- 125. РЕШЕНИЯ
- 126. U Записать функцию тока для вихревой пары в потоке жидкости, имеющего постоянную скоростью U. Скорость потока
- 127. Найти в ортогональной системе координат уравнения линий тока для 1) случая двух вихрей одинаковой интенсивности 2)
- 129. Скачать презентацию
















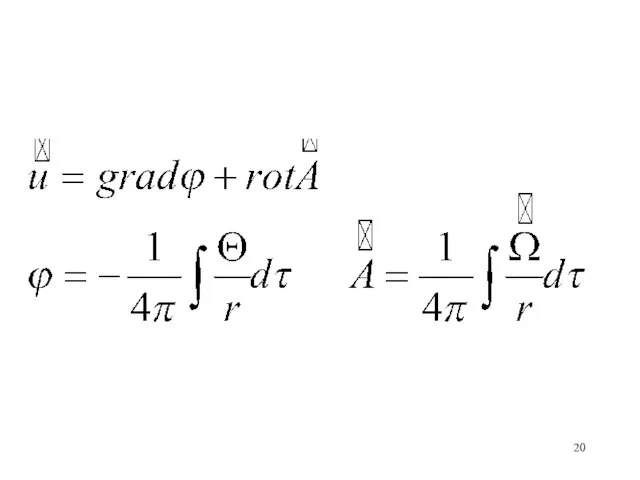
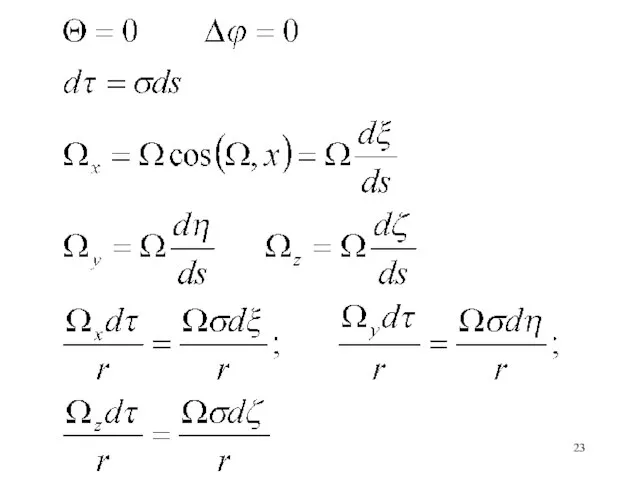
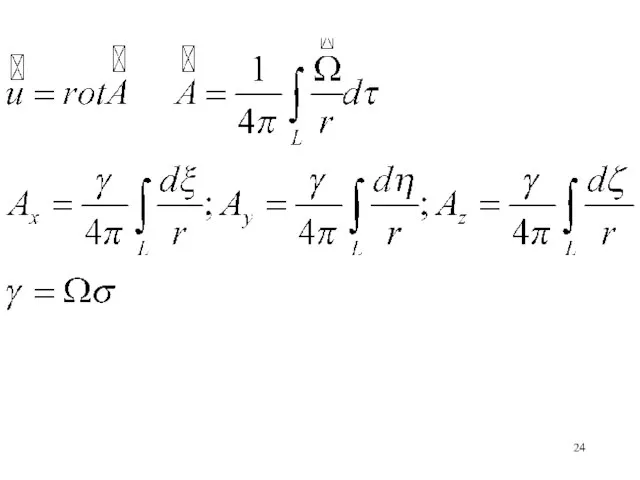
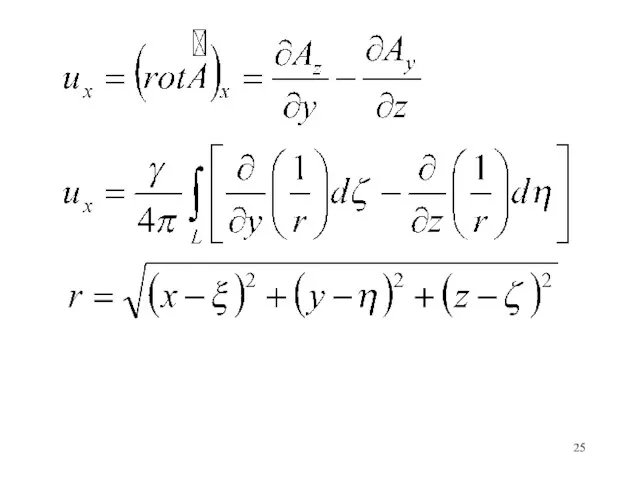
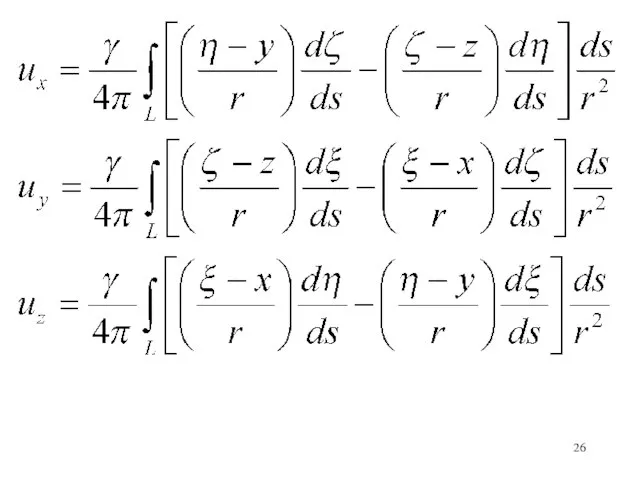






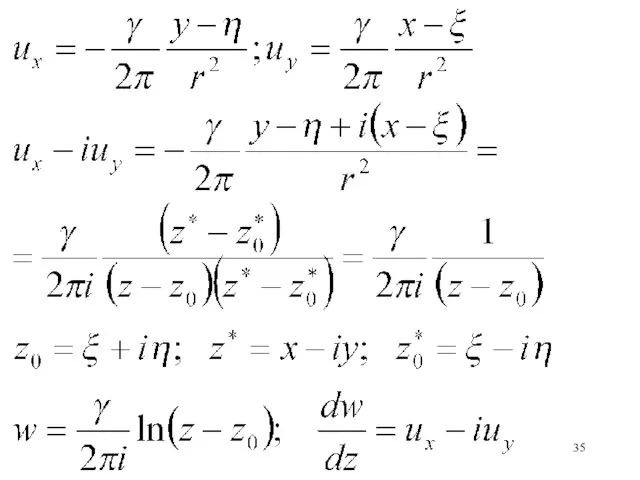

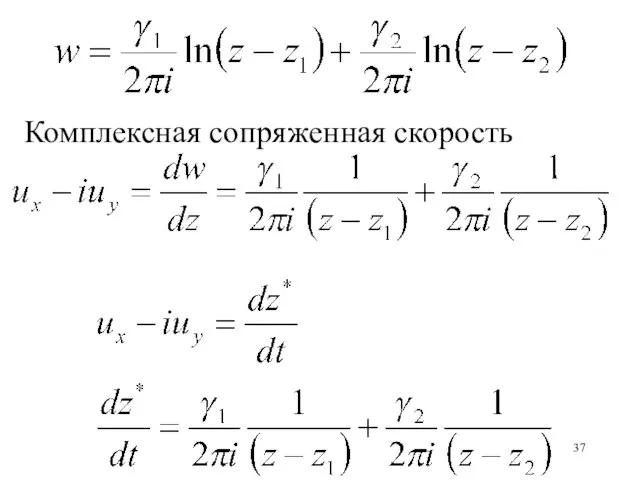

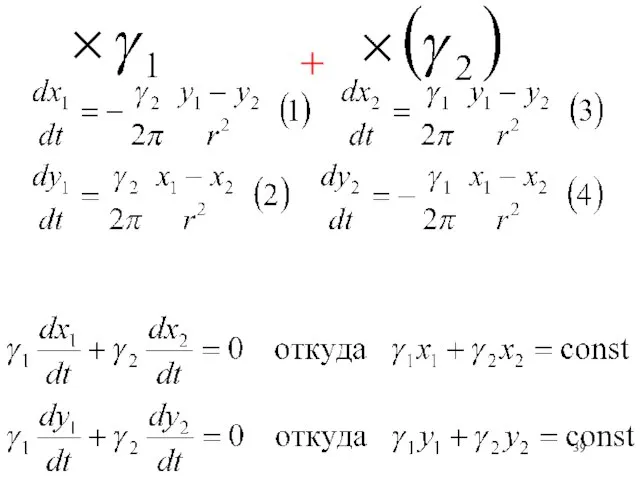















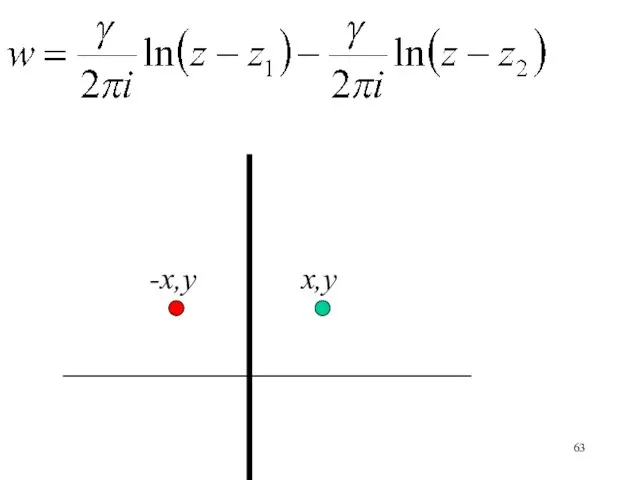

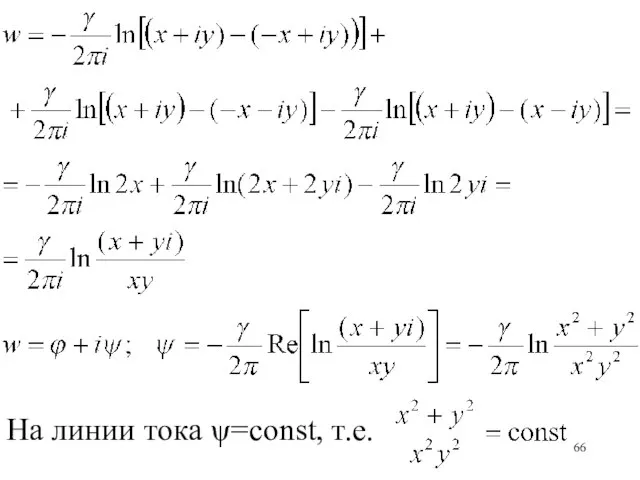






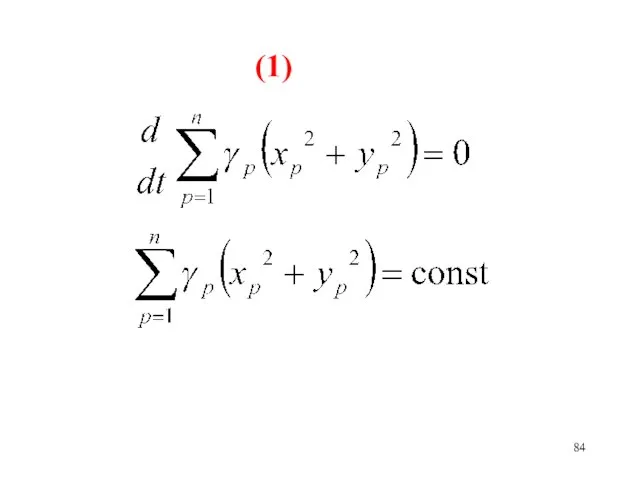





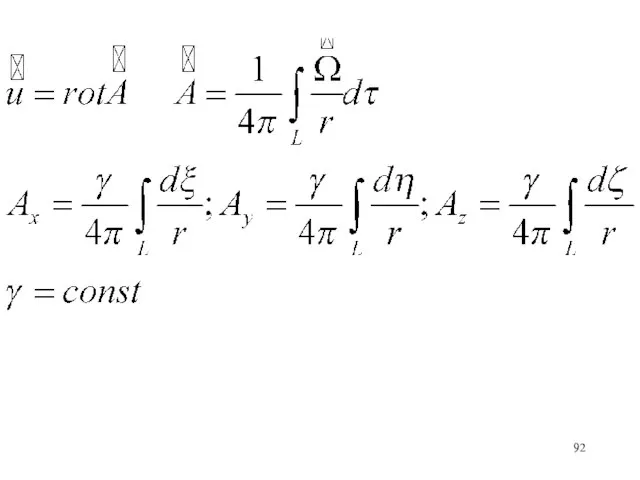


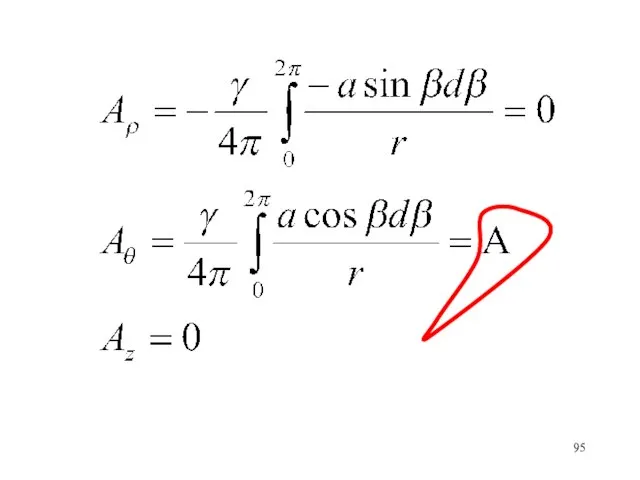



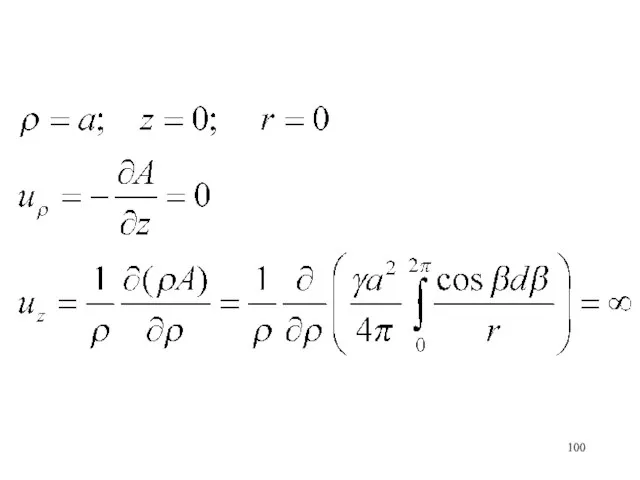









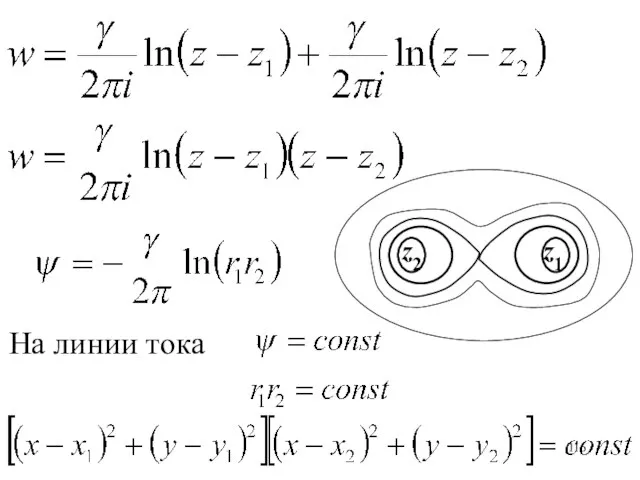



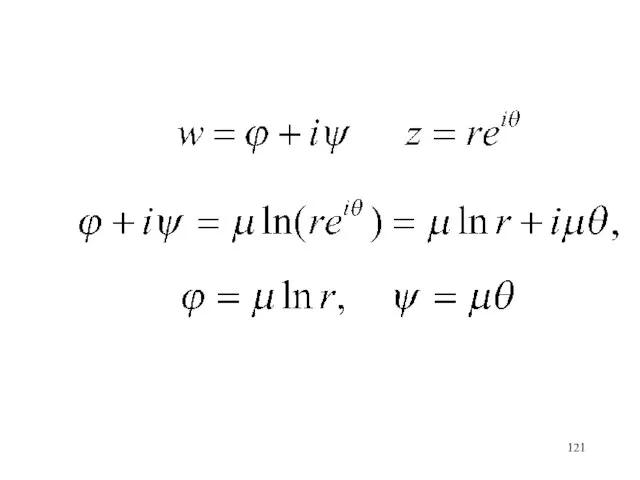



 Учебный Центр БИТ
Учебный Центр БИТ Торф
Торф Представление корректирующих сведений персонифицированного учета
Представление корректирующих сведений персонифицированного учета Voľba študijného odboru
Voľba študijného odboru Технология .NET Remoting
Технология .NET Remoting Награды в сфере нанотехнологий
Награды в сфере нанотехнологий Global Trading St. Petersburg
Global Trading St. Petersburg Калькуляция
Калькуляция Python_-_задача_на_пару__HiNjSk
Python_-_задача_на_пару__HiNjSk Музыка эпохи классицизма
Музыка эпохи классицизма Международная транспортная инфраструктура, региональная интеграция и развитие (на примере Украины)
Международная транспортная инфраструктура, региональная интеграция и развитие (на примере Украины) Формирование международной проектной команды для выполнения многоцелевого проекта в области ИТ. Игорь Ковалев Директор по ИТ про
Формирование международной проектной команды для выполнения многоцелевого проекта в области ИТ. Игорь Ковалев Директор по ИТ про Оплата частями от Target Finance
Оплата частями от Target Finance AutoProcessor UPGRADED Integration
AutoProcessor UPGRADED Integration Гидромеханические установки. Цилиндроконический гидроциклон. (Лекция 5)
Гидромеханические установки. Цилиндроконический гидроциклон. (Лекция 5) Old English Grammar
Old English Grammar Равновесие тел
Равновесие тел Казахские национальные блюда
Казахские национальные блюда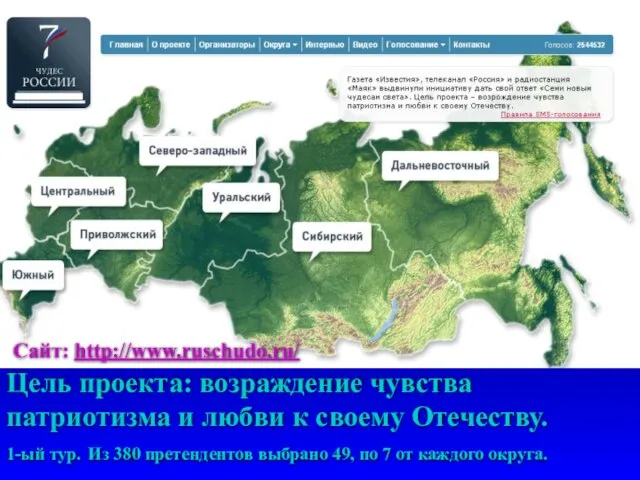 Сайт: http://www.ruschudo.ru/ Цель проекта: возраждение чувства патриотизма и любви к своему Отечеству.1-ый тур. Из 380 претендентов выбрано 49,
Сайт: http://www.ruschudo.ru/ Цель проекта: возраждение чувства патриотизма и любви к своему Отечеству.1-ый тур. Из 380 претендентов выбрано 49,  «Виды речевых нарушений у дошкольников»
«Виды речевых нарушений у дошкольников» Maxim Calujac
Maxim Calujac Проектирование образовательных кейсов с использованием дистанционных технологий
Проектирование образовательных кейсов с использованием дистанционных технологий Геополитика Узбекистана
Геополитика Узбекистана Юдина Татьяна Владимировна
Юдина Татьяна Владимировна Презентация на тему Различные группы антибиотиков: характеристика, получение, применение
Презентация на тему Различные группы антибиотиков: характеристика, получение, применение  Использование технологии развития критического мышления на уроке английского языка по теме:«Телевидение: за и против».
Использование технологии развития критического мышления на уроке английского языка по теме:«Телевидение: за и против». Пейзаж в линейной перспективе
Пейзаж в линейной перспективе игра
игра