Содержание
- 2. Понятие вектора Вектор – отрезок, для которого указано, какой из его концов считается началом, а какой
- 3. Понятие вектора Под длиной ненулевого вектора понимают длину отрезка АВ. Обозначение: | |, |a| Длина нулевого
- 4. Коллинеарность векторов Ненулевые вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
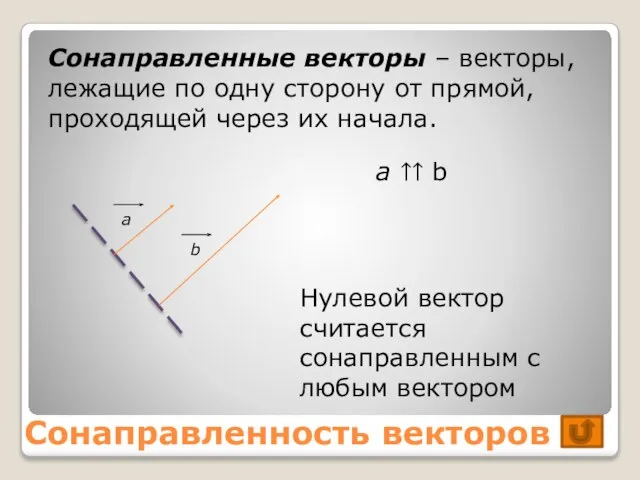
- 5. Сонаправленность векторов Сонаправленные векторы – векторы, лежащие по одну сторону от прямой, проходящей через их начала.
- 6. Противоположная направленность векторов Противоположно направленные векторы – векторы, лежащие по разные стороны от прямой, проходящей через
- 7. Равенство векторов М N
- 8. Противоположность векторов Вектора называются противоположными, если они противоположно направленны и их длины равны.
- 9. Проверь себя! ОТВЕТЫ
- 10. ОТВЕТЫ да; нет, могут быть противоположно направленными; да; нет, вектора могут иметь разную длину; да.
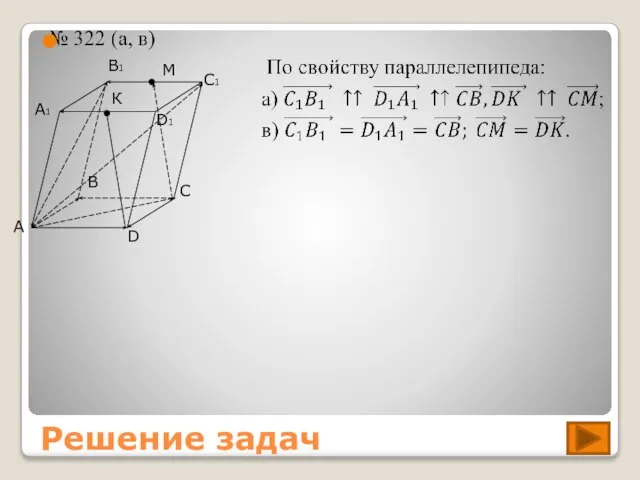
- 11. Решение задач D A B C M N K
- 12. Решение задач M К
- 13. Домашнее задание § 1 (с. 84-85), № 320 (б), 321 (а), 322 (б), 326 (а, б).
- 15. Скачать презентацию










 Занятие 1
Занятие 1 Пролегомены к теории языка
Пролегомены к теории языка Метод проектов в работе учителя
Метод проектов в работе учителя Искусство и власть: их влияние друг на друга и взаимодействие
Искусство и власть: их влияние друг на друга и взаимодействие Орфографическая диктовка
Орфографическая диктовка "О вреде курения"
"О вреде курения" Изменения 2012 в трудовом законодательстве
Изменения 2012 в трудовом законодательстве Россия в XVII веке
Россия в XVII веке Что_будет_с_рынком_недвижимости_часть_2
Что_будет_с_рынком_недвижимости_часть_2 Ваш текст. Шаблон
Ваш текст. Шаблон Покрытия Caparol для промышленных полов со специальными требованиями
Покрытия Caparol для промышленных полов со специальными требованиями ПРЕЗЕНТАЦИЯ ПО ПСИХОЛОГИИ
ПРЕЗЕНТАЦИЯ ПО ПСИХОЛОГИИ ЕДИНЫЙ ГОСУДАРСТВЕННЫЙ ЭКЗАМЕНЛИТЕРАТУРА2 часть
ЕДИНЫЙ ГОСУДАРСТВЕННЫЙ ЭКЗАМЕНЛИТЕРАТУРА2 часть Создание мультимедийных презентаций
Создание мультимедийных презентаций Стиль Luxe purism
Стиль Luxe purism Живые существа. Группы живых существ (3 класс)
Живые существа. Группы живых существ (3 класс) Макроэкономическая политика
Макроэкономическая политика Белорусская жемчужина в коллекции Козелл-Поклевских
Белорусская жемчужина в коллекции Козелл-Поклевских Организация деятельности социально-педагогического и медико-психологического центра на основе народных традиций
Организация деятельности социально-педагогического и медико-психологического центра на основе народных традиций Презентация на тему Подтип Позвоночные Рыбы
Презентация на тему Подтип Позвоночные Рыбы  Семантика орнаментальных узоров ханты и манси
Семантика орнаментальных узоров ханты и манси HYDE PARK
HYDE PARK Тамбовский вклад в русскую культуру в первой половине 19 века
Тамбовский вклад в русскую культуру в первой половине 19 века Краткая информация по рынку агрострахования в 2010 годуwww.agroins.com.ua Ирина ГринюкЗаместитель руководителя Проекта“Развитие агро
Краткая информация по рынку агрострахования в 2010 годуwww.agroins.com.ua Ирина ГринюкЗаместитель руководителя Проекта“Развитие агро Творческий проект «Сердце из роз»
Творческий проект «Сердце из роз» Классный час «Поговорим о доброте»
Классный час «Поговорим о доброте» Бизнес-симулятор
Бизнес-симулятор Портфолио – профессиональный портрет библиотекаря образовательного учреждения
Портфолио – профессиональный портрет библиотекаря образовательного учреждения