Содержание
- 2. доцент кафедры математического образования Батан Любовь Федоровна учитель математики первой квалификационной категории МОУ лицей № 176
- 3. Аннотация Урок алгебры рекомендован для учащихся 10 класса, обучающихся по учебнику «Алгебра и математический анализ» для
- 4. Актуальность Данная тема является очень важной и значимой, т. к. в материалах ЕГЭ большое внимание уделяется
- 5. Тип урока Урок закрепления изученного материала в форме самостоятельной групповой работы по карточкам Оборудование: Smart-доска; Сканер;
- 6. Цели урока Для учителя Для ученика
- 7. Цели урока Обобщить и закрепить свои знания и умения при построении графика функции с помощью ее
- 8. Цели урока Систематизировать, обобщить и расширить знания и умения учащихся при построении графиков функций. Развивать умения
- 9. Задачи урока Формировать устойчивый интерес к математике через дифференцированный подход к учащимся. Вовлекать каждого ученика в
- 10. Содержание урока Вводная беседа. Устная работа. Самостоятельная работа в группах. Обобщение. Итог. Историческая справка. Рефлексия.
- 11. На уроке мы должны закрепить и обобщить свои знания и умения при построении графика функции с
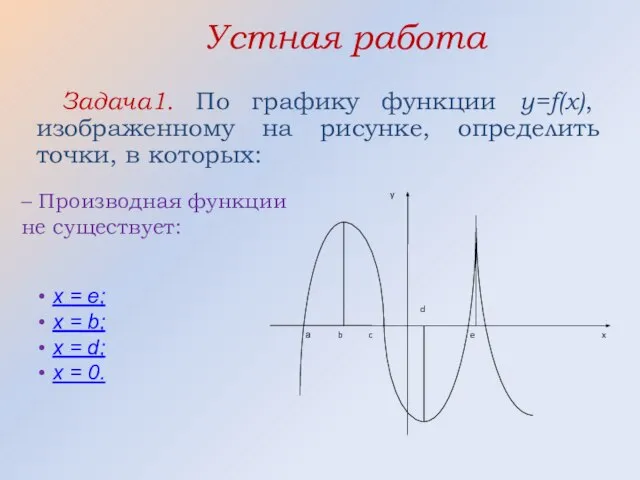
- 12. Устная работа Задача1. По графику функции y=f(x), изображенному на рисунке, определить точки, в которых: – Производная
- 13. Устная работа Задача1. По графику функции y=f(x), изображенному на рисунке, определить точки, в которых: – Производная
- 14. Устная работа Задача1. По графику функции y=f(x), изображенному на рисунке, определить: – Точки максимума функции: x
- 15. Устная работа Задача1. По графику функции y=f(x), изображенному на рисунке, определить: – промежутки убывания функции: [b;d]
- 16. Устная работа Задача1. По графику функции y=f(x), изображенному на рисунке, определить: – Промежутки возрастания функции: [b;d]
- 17. Отлично! Далее
- 18. Подумай ещё!
- 19. Отлично! Далее
- 20. Подумай ещё!
- 21. Отлично! Далее
- 22. Подумай ещё!
- 23. Отлично! Далее
- 24. Подумай ещё!
- 25. Отлично! Далее
- 26. Подумай ещё!
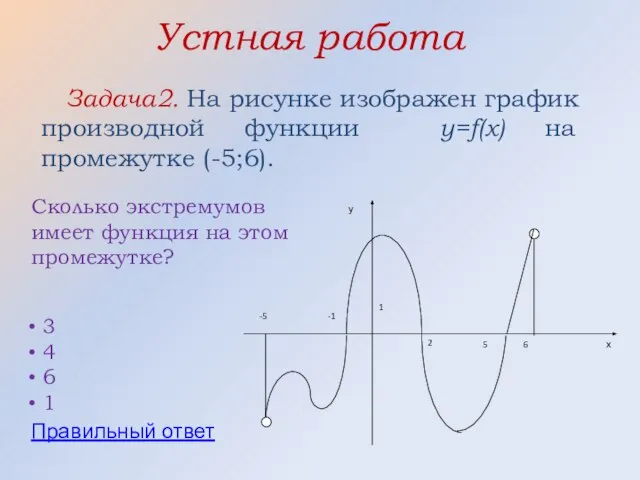
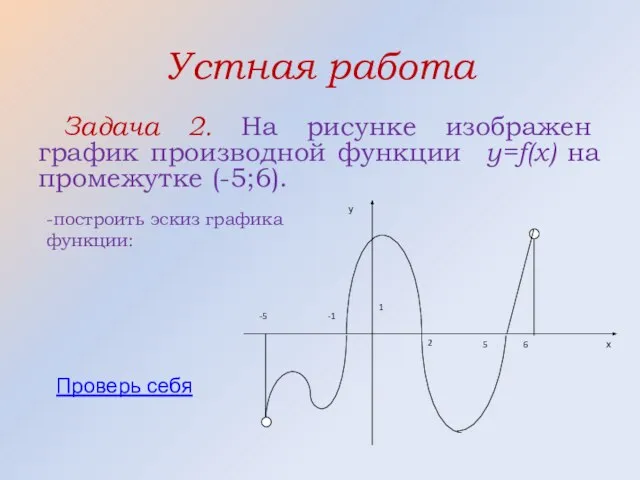
- 27. Устная работа Задача2. На рисунке изображен график производной функции y=f(x) на промежутке (-5;6). Сколько экстремумов имеет
- 28. Правильный ответ 3
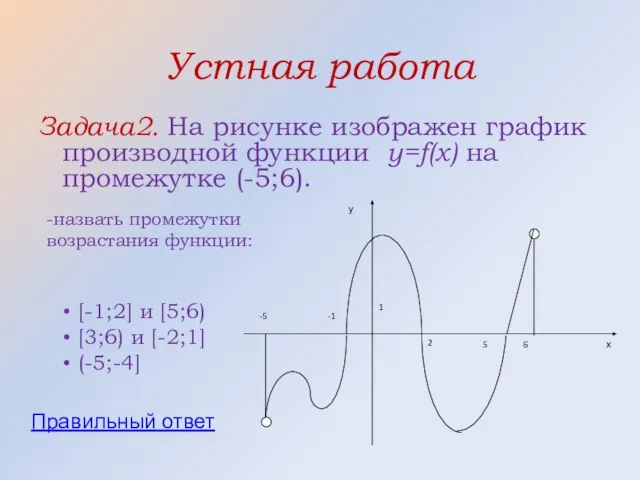
- 29. Устная работа Задача2. На рисунке изображен график производной функции y=f(x) на промежутке (-5;6). -назвать промежутки возрастания
- 30. Правильный ответ [-1;2] и [5;6)
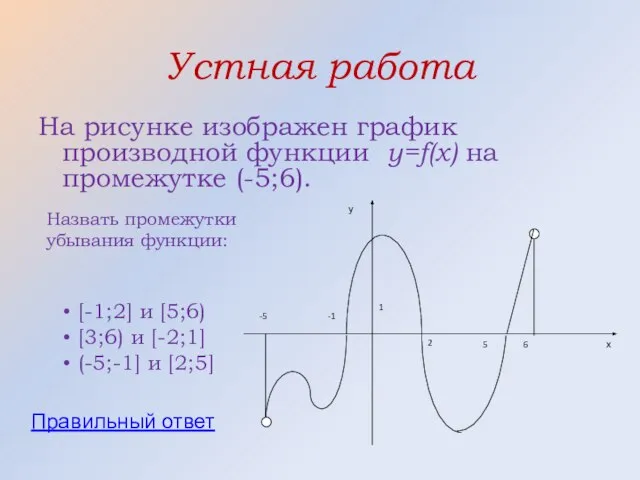
- 31. Устная работа На рисунке изображен график производной функции y=f(x) на промежутке (-5;6). Назвать промежутки убывания функции:
- 32. Правильный ответ (-5;-1] и [2;5]
- 33. Устная работа Задача 2. На рисунке изображен график производной функции y=f(x) на промежутке (-5;6). -построить эскиз
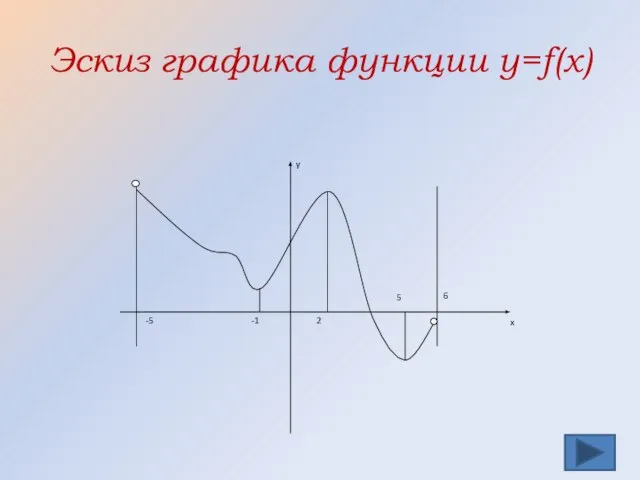
- 34. Эскиз графика функции y=f(x)
- 35. Устная работа Задача3. Найти асимптоты графика функции Проверь себя
- 36. Ответ х=2 – вертикальная асимптота у=х – наклонная асимптота
- 37. Самостоятельная работа учащихся Класс делится на 3 группы. Каждая группа учащихся получает задание на карточке. Первая
- 38. Уровни базовый уровень основной уровень продвинутый уровень
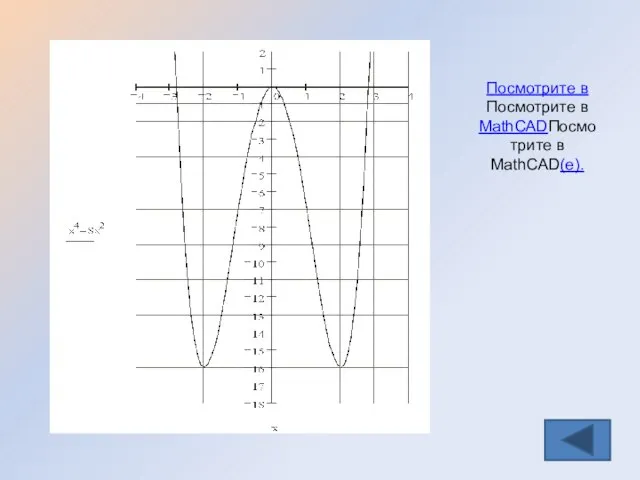
- 39. Задание группе 1 Базовый уровень: Исследовать функцию и построить ее график у = x4 – 8x2
- 40. Задание группе 2 Основной уровень: Исследовать функцию и построить ее график Проверь себя Назад Справка
- 41. Задание группе 3 Продвинутый уровень: Исследовать функцию и построить ее график Проверь себя Назад Справка
- 42. Вспомните план исследования: 1.Область определения функции. 2.Множество значений функции. 3.Чётность. 4.Периодичность. 5.Первая производная: по ней определяются
- 43. Вспомните план исследования: 1.Область определения функции. 2.Множество значений функции. 3.Чётность. 4.Периодичность. 5.Первая производная: по ней определяются
- 44. Вспомните план исследования: 1.Область определения функции. 2.Множество значений функции. 3.Чётность. 4.Периодичность. 5.Первая производная: по ней определяются
- 45. Проверь себя Замечаем, что функция четная и ее график симметричен оси ОУ, достаточно исследовать ее на
- 46. Посмотрите в Посмотрите в MathCADПосмотрите в MathCAD(е).
- 47. Ответить, используя график, на вопросы: 1. Сколько критических точек имеет функция ? 2. Чему равна точка
- 48. Ответить, используя график, на вопросы: 1. Сколько критических точек имеет функция ? ( 3 ) 2.
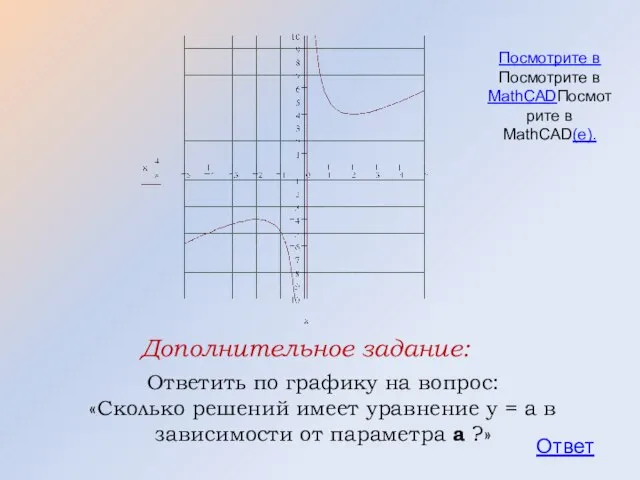
- 49. Ответить по графику на вопрос: «Сколько решений имеет уравнение у = а в зависимости от параметра
- 50. Ответ: Если а = ± 4, то одно решение. Если |а| > 4, то два решения.
- 51. Обобщение Графики функций можно строить «по точкам». Однако при таком способе построения можно пропустить важные особенности
- 52. Итог Вот что сказал Декарт по поводу методов: «Под методом же я разумею точные и простые
- 53. Математика развивалась стремительно, но без понятия производной многие исследования не имели смысла. В 1679 году Пьер
- 54. Исследуя функцию с помощью производной, я научился находить : Область определения функции; Определять четность функции; Критические
- 55. Спасибо за урок До свидания!!! Удачи вам!!!
- 57. Скачать презентацию

























![Правильный ответ [-1;2] и [5;6)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/319335/slide-29.jpg)
![Правильный ответ (-5;-1] и [2;5]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/319335/slide-31.jpg)



















 Паспорт объекта сети Харьковская региональная дирекция
Паспорт объекта сети Харьковская региональная дирекция Презентация на тему Средства для борьбы с насекомыми
Презентация на тему Средства для борьбы с насекомыми Задачи и методы современной психологии
Задачи и методы современной психологии Подходы к моделированию ГРА
Подходы к моделированию ГРА Технология продуктивного чтения или формирование типа правильной читательской деятельности
Технология продуктивного чтения или формирование типа правильной читательской деятельности Заработать в интернете без вложений и без продаж
Заработать в интернете без вложений и без продаж Понятие стратегического менеджмента
Понятие стратегического менеджмента Ультразвуковой уровнемер на микроконтроллере PIC16F628
Ультразвуковой уровнемер на микроконтроллере PIC16F628 Роза из бумаги
Роза из бумаги ОАО «Противокарстовая и береговая защита» 606019, Нижегородская обл., г.Дзержинск, ул.Гастелло, 10/15 Тел./факс (8313) 25-98-01 E-mail:
ОАО «Противокарстовая и береговая защита» 606019, Нижегородская обл., г.Дзержинск, ул.Гастелло, 10/15 Тел./факс (8313) 25-98-01 E-mail:  Готовимся к части С
Готовимся к части С EBG Customer Training Map
EBG Customer Training Map Виды и назначение технологических карт
Виды и назначение технологических карт Учредитель: Администрация Городского округа «Город Волжск». Адрес:425000, ул. Коммунистическая, д.1.
Учредитель: Администрация Городского округа «Город Волжск». Адрес:425000, ул. Коммунистическая, д.1. Презентация на тему Русь и Золотая Орда (6 класс)
Презентация на тему Русь и Золотая Орда (6 класс) Анализ системы подготовки и аттестации кадров предприятия туризма. Задание 5
Анализ системы подготовки и аттестации кадров предприятия туризма. Задание 5 Нетрадиционная техника рисования граттаж Праздничный салют
Нетрадиционная техника рисования граттаж Праздничный салют сочинение
сочинение Проект « Профессии наших родителей»
Проект « Профессии наших родителей» Натюрморт
Натюрморт Ц у н а м и
Ц у н а м и Публичная презентация результатов педагогической деятельностии инновационной работыучителя начальных классов МКОУ «Лицей се
Публичная презентация результатов педагогической деятельностии инновационной работыучителя начальных классов МКОУ «Лицей се Психологический климат в семье (8 класс)
Психологический климат в семье (8 класс) Игры с залом PowerPoint
Игры с залом PowerPoint Кулинарный поединок
Кулинарный поединок Food rap
Food rap ЗУП КОРП: реализованная функциональность и выпуск конфигурации Докладчик: Лохтин Т.О.
ЗУП КОРП: реализованная функциональность и выпуск конфигурации Докладчик: Лохтин Т.О. Правила судейства игры Баскетбол
Правила судейства игры Баскетбол