Содержание
- 2. Проверка домашней работы № 198а x y -1
- 3. № 200в
- 4. Устно
- 5. 22.02.2010г. Формулы дифференцирования. Значения функции в данной точке:
- 6. Значения производной функции в этой точке:
- 7. Производная суммы равна сумме производных.
- 8. Лемма: Если функция f дифференцируема в точке х, то она непрерывна в этой точке.
- 9. Постоянный множитель можно выносить за знак производной.
- 12. Решение упражнений № 208б,г № 209а Самостоятельно с последующей проверкой № 209в № 209г
- 16. Скачать презентацию

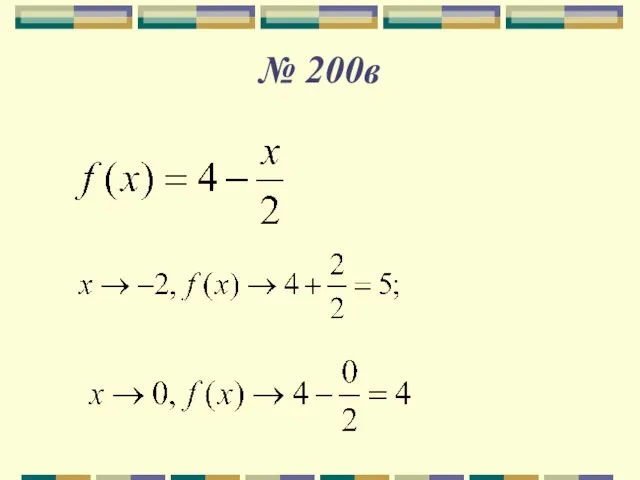






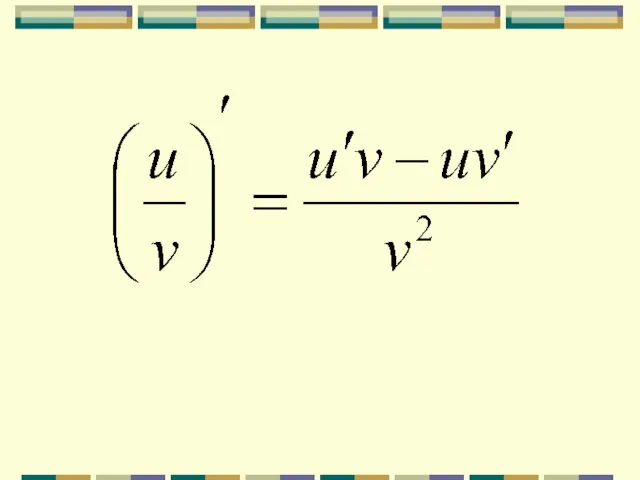
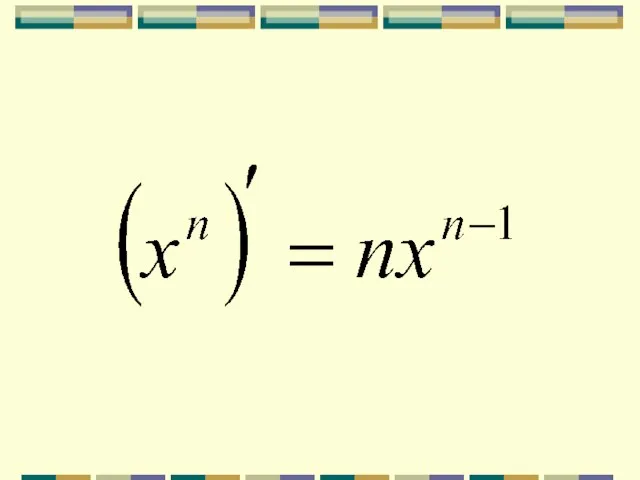



 Lluvia
Lluvia Жужжалочка. Дидактическая игра для автоматизации звука Ж в словах
Жужжалочка. Дидактическая игра для автоматизации звука Ж в словах УД ПСИХОЛОГИЯ
УД ПСИХОЛОГИЯ Храмы России
Храмы России Оптическая микроскопия
Оптическая микроскопия Менеджмент
Менеджмент Кондитерский отдел
Кондитерский отдел Органы и службы стандартизации РФ
Органы и службы стандартизации РФ Вышел зайчик погулять Художник – В. Сергеев
Вышел зайчик погулять Художник – В. Сергеев Знакомство с точкой
Знакомство с точкой Состояние и задачи управления проектами в строительстве
Состояние и задачи управления проектами в строительстве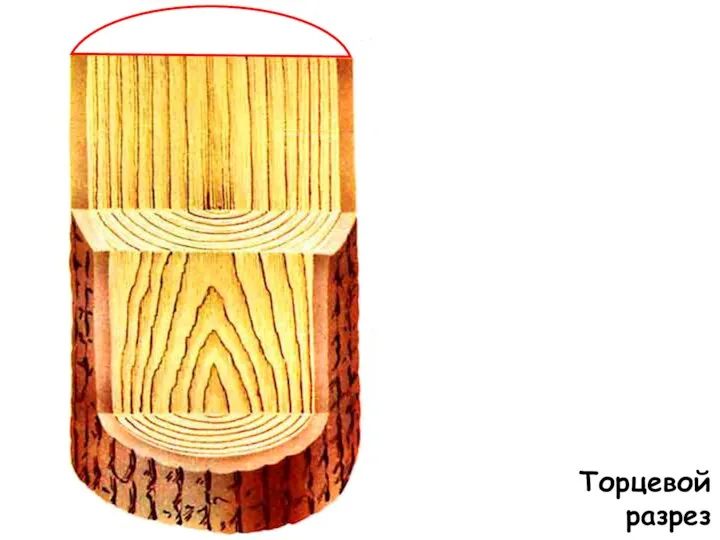 Торцевой разрез. Материаловедение
Торцевой разрез. Материаловедение чайные истории
чайные истории Шпаргалка юного покупателя
Шпаргалка юного покупателя Учебно-методический комплекс "Живая география" Живая география - учебно-методический комплекс, позволяющий использовать геоинфор
Учебно-методический комплекс "Живая география" Живая география - учебно-методический комплекс, позволяющий использовать геоинфор Классификация реакций
Классификация реакций Организация хранения документов Архивного фонда Российской Федерации и других архивных документов
Организация хранения документов Архивного фонда Российской Федерации и других архивных документов Трансляция – биосинтез белка на рибосоме
Трансляция – биосинтез белка на рибосоме Инновационный подход к жизни
Инновационный подход к жизни DaCoPAn Software Engineering Project - Система динамической визуализации событий работы протоколов при обмене данными между двумя сетевыми ЭВМ — D
DaCoPAn Software Engineering Project - Система динамической визуализации событий работы протоколов при обмене данными между двумя сетевыми ЭВМ — D Урок – размышление по рассказу К.Г. Паустовского «Телеграмма»
Урок – размышление по рассказу К.Г. Паустовского «Телеграмма» Путешествие в мир животных
Путешествие в мир животных СПАСИБО, АЗБУКА!
СПАСИБО, АЗБУКА! Rave Cosmology Today Dying, Death & Bardo . RC3.8
Rave Cosmology Today Dying, Death & Bardo . RC3.8 Основные закономерности развития информационного пространства
Основные закономерности развития информационного пространства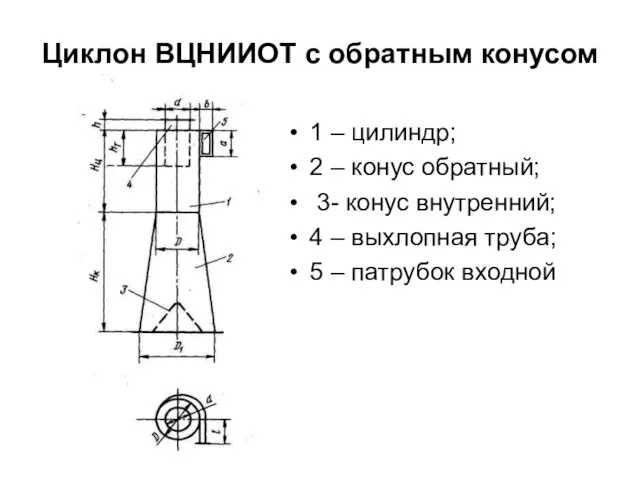 Циклон ВЦНИИОТ с обратным конусом
Циклон ВЦНИИОТ с обратным конусом  Квантовые компьютеры
Квантовые компьютеры Разработать рекламную кампанию в стиле шоу для молодежного интернет-издания Пи-Пермь (бюджет студенческой редакции)
Разработать рекламную кампанию в стиле шоу для молодежного интернет-издания Пи-Пермь (бюджет студенческой редакции)