Содержание
- 2. © ElVisti Правило Парето Анаизируя общественные процессы, Парето рассматривал социальную среду как пирамиду, наверху которой находятся
- 3. © ElVisti Распределение Парето Распределение доходов по Парето описывается уравнением: N = A /Х p+1, где
- 4. © ElVisti Интерпретации правила Парето Замеченное правило применимо и в очень многих областях и сформулировал правило,
- 5. © ElVisti Цена 5 процентов качества Если предположить, что идеальная система имеет 100% необходимых функций, а
- 6. © ElVisti О переходе количества в качество Если система достигла 99% своей идеальной функциональности, то дальнейшие
- 7. © ElVisti Буква S технологического прогресса В то же время, реализация новых подходов приводит к появлению
- 8. © ElVisti Буква S развития интернет-технологий В качестве примера этой закономерности можно привести развитие сети Интернет,
- 9. © ElVisti Законы Зипфа При статистическом описании распределения слов по частоте их употребления в тексте (как,
- 10. © ElVisti Законы Зипфа Зипф сформулировал еще одну закономерность, состоящую в том, что частота и количество
- 11. © ElVisti Закономерность Брэдфорда Основной смысл закономерности С. Брэдфорда заключается в следующем: если научные журналы расположить
- 12. © ElVisti Закон Хипса В компьютерной лингвистике эмпирический закон Хипса связывает объем документа с объемом словаря
- 13. © ElVisti Прогноз Мура и информационная сфера Прогноз Мура родился как прогноз развития технологии микросхем. В
- 14. © ElVisti Прогноз Мура и информационная сфера Сегодня прогноз Мура распространяется на все большее количество областей.
- 16. Скачать презентацию
Слайд 2© ElVisti
Правило Парето
Анаизируя общественные процессы, Парето рассматривал социальную среду как пирамиду,
© ElVisti
Правило Парето
Анаизируя общественные процессы, Парето рассматривал социальную среду как пирамиду,

Вильфредо Парето
Слайд 3© ElVisti
Распределение Парето
Распределение доходов по Парето описывается уравнением:
N =
© ElVisti
Распределение Парето
Распределение доходов по Парето описывается уравнением:
N =

где Х – величина дохода, N - численность людей с доходом, равным или выше Х, A и p - коэффициенты уравнения.
В математической статистике это распределение получило имя Парето, при этом естественные ограничения на коэффициенты: Х ≥1, p > 0.
Распределение Парето обладает свойством устойчивости, т.е. сумма двух случайных переменных, имеющих распределение Парето, также будет иметь это распределение.
Определение
распределения
Парето в
математической
статистике*:
__________
*Источник:
Википедия
Слайд 4© ElVisti
Интерпретации правила Парето
Замеченное правило применимо и в очень многих
© ElVisti
Интерпретации правила Парето
Замеченное правило применимо и в очень многих

При реализации систем массового обслуживания, в том числе и поисковых систем, необходимо учитывать то, что наиболее сложным функциональным возможностям системы, на реализацию которых ушло 80 и более процентов трудозатрат будут использоваться не более, чем 20% пользователей данной системы.
Слайд 5© ElVisti
Цена 5 процентов качества
Если предположить, что идеальная система имеет
© ElVisti
Цена 5 процентов качества
Если предположить, что идеальная система имеет

Это утверждение можно также рассматривать как следствие закона Парето в интерпретации причина-следствие. Повысить функциональность системы, работающей в 90% предельных возможностей, до 95% (следствие) потребует удвоения усилилий (причины). Конечно же соотношение 90-95 весьма приблизительно, но тенденция прекрасно видна по типовой диаграмме Парето или графику соответствующей функции распределения.
Проявления эффекта 5% на практике встречаются повсеместно. Например, при появлении новых поисковых систем в Интернете. Казалось бы, вновь появившаяся система вот-вот должна превзойти такие бренды, как Yahoo! или Google и осталось совсем немного, 5-10% функциональности, можно прогнозировать, что скорее всего этого не произойдет, ведь понадобятся еще капиталовложения, превосходящие уже вложенные средства на создание "рабочей модели" новой системы.
Слайд 6© ElVisti
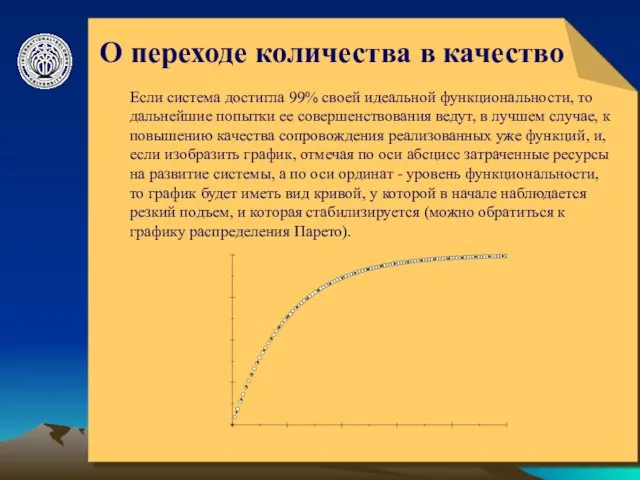
О переходе количества в качество
Если система достигла 99% своей идеальной
© ElVisti
О переходе количества в качество
Если система достигла 99% своей идеальной
Слайд 7© ElVisti
Буква S технологического прогресса
В то же время, реализация новых
© ElVisti
Буква S технологического прогресса
В то же время, реализация новых

В реальной жизни бывают случаи, когда после длительного процесса стабилизации происходит резкий взлет этой кривой выше уровня 100%, т.е. график принимает вид перевернутой буквы S. С чем же может быть связан такой подъем, когда функциональность резко превышает "идеальную" 100-процентную? Этот феномен обычно бывает связан с появлением новых подходов и взглядов на ставшие уже традиционными устоявшиеся процессы.
Слайд 8© ElVisti
Буква S развития
интернет-технологий
В качестве примера этой закономерности можно
© ElVisti
Буква S развития
интернет-технологий
В качестве примера этой закономерности можно

Несмотря на то, что существовали такие информационные службы, как Usenet, Ftp, Gopher, до 90-х годов Сеть решала свои главные задачи, обеспечивая электронную связь между научными, общественными, государственными организациями и частными лицами. К этому времени Интернет существовал уже свыше 15-ти лет и стабилизировалась в своем развитии, в частности, по числу абонентов.
Феномен появления и развития Web-технологий привел к тому, что за следующие 10 лет сеть Интернет стала крупнейшим информационным ресурсом в мире, число абонентов которой превысило миллиард человек.
Слайд 9© ElVisti
Законы Зипфа
При статистическом описании распределения слов по частоте их употребления
© ElVisti
Законы Зипфа
При статистическом описании распределения слов по частоте их употребления

Джордж Зипф экспериментально показал, что распределение слов естественного языка подчиняется закону, который можно сформулировать следующим образом. Если к какому-либо достаточно большому тексту составить список всех встретившихся в нем слов, а затем отранжировать эти слова в порядке убывания частоты их встречаемости в тексте, то для любого слова произведение его ранга и частоты встречаемости будет величиной постоянной: f * r = c, где f - частота встречаемости слова в тексте; r - ранг слова в списке; с - эмпирическая постоянная величина. Для русского и украинского языков коэффициенты Зипфа составляю приблизительно 0,06-0,07.
Слайд 10© ElVisti
Законы Зипфа
Зипф сформулировал еще одну закономерность, состоящую в том,
© ElVisti
Законы Зипфа
Зипф сформулировал еще одну закономерность, состоящую в том,
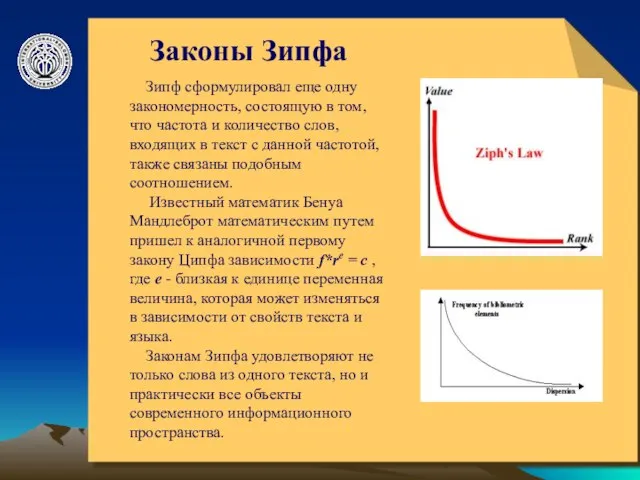
Известный математик Бенуа Мандлеброт математическим путем пришел к аналогичной первому закону Ципфа зависимости f*re = c , где e - близкая к единице переменная величина, которая может изменяться в зависимости от свойств текста и языка.
Законам Зипфа удовлетворяют не только слова из одного текста, но и практически все объекты современного информационного пространства.
Слайд 11© ElVisti
Закономерность Брэдфорда
Основной смысл закономерности С. Брэдфорда заключается в
© ElVisti
Закономерность Брэдфорда
Основной смысл закономерности С. Брэдфорда заключается в

P3 : P2 = P2 : P1 = N,
где P1 - число журналов в 1-й зоне, P2 - во 2-й, P3 - число журналов в 3-й зоне. Закономерность Брэдфорда изначально рассматривалась как специфический случай распределения Зипфа для системы периодических изданий по науке и технике. Исходя из реалий развития сети Интернет, ее можно рассматривать как закономерность, относящуюся к ранговому распределению Web-сайтов, относительно вхождения в них Web-страниц, релевантных некоторой области знаний.
Слайд 12© ElVisti
Закон Хипса
В компьютерной лингвистике эмпирический закон Хипса связывает объем
© ElVisti
Закон Хипса
В компьютерной лингвистике эмпирический закон Хипса связывает объем

v(n) = Knβ,
где v – это объем словаря уникальных слов, составленный из текста, который состоит из n уникальных слов. K и β – обусловленные эмпирически параметры. Для европейских языков K принимает значение от 10 до100, а β - от 0.4 до 0.6.
Закон Хипса справедлив не только для уникальных слов, но и для многих других информационных объектов, описываемых не экспоненциальной, а степенной зависимостью.
Слайд 13© ElVisti
Прогноз Мура и информационная сфера
Прогноз Мура родился как
© ElVisti
Прогноз Мура и информационная сфера
Прогноз Мура родился как

Гордон Мур,
www.intel.com
Слайд 14© ElVisti
Прогноз Мура и информационная сфера
Сегодня прогноз Мура распространяется
© ElVisti
Прогноз Мура и информационная сфера
Сегодня прогноз Мура распространяется

Развитие коммуникационных возможностей приводит к росту количества доступной информации, в частности в Интернет. С другой стороны, увеличение объемов доступного контента способствует росту инновационной деятельности, все больше знаний, необходимых для исследовательских работ, публикуется в Сети, тем самым, способствуя технологическому прогрессу, на котором основывается прогноз Мура.
 Классификация методов и технологий обучения в ВУЗе
Классификация методов и технологий обучения в ВУЗе Манипуляция
Манипуляция Казанский монастырь
Казанский монастырь ВЕСНЯНІ КВІТИ
ВЕСНЯНІ КВІТИ Уполномоченный орган по защите прав субъектов персональных данных
Уполномоченный орган по защите прав субъектов персональных данных Инструменты и приборы
Инструменты и приборы Учебный план профильного обучения Методические аспекты составления в условиях перехода
Учебный план профильного обучения Методические аспекты составления в условиях перехода Рефлексивная деятельность -основа развития профессиональной компетентности учителя
Рефлексивная деятельность -основа развития профессиональной компетентности учителя The healthy way of life
The healthy way of life ОЦЕНКА КАЧЕСТВА ОТЧЕТНОЙ ДОКУМЕНТАЦИИ ПО ОНКОЛОГИИСТАТИСТИЧЕСКИЙ УЧЕТ И ОТЧЕТНОСТЬ В УЧРЕЖДЕНИЯХ ОНКОЛОГИЧЕСКОГО ПРОФИЛЯ
ОЦЕНКА КАЧЕСТВА ОТЧЕТНОЙ ДОКУМЕНТАЦИИ ПО ОНКОЛОГИИСТАТИСТИЧЕСКИЙ УЧЕТ И ОТЧЕТНОСТЬ В УЧРЕЖДЕНИЯХ ОНКОЛОГИЧЕСКОГО ПРОФИЛЯ Проценты
Проценты Деревья (2 класс)
Деревья (2 класс) Цикл уроков по разделу Антарктида
Цикл уроков по разделу Антарктида Международное право и документы о защите жертв вооруженных конфликтов
Международное право и документы о защите жертв вооруженных конфликтов Риск-менеджмент. Лекция №4
Риск-менеджмент. Лекция №4 Преобразования на Руси в области культуры при Петре 1
Преобразования на Руси в области культуры при Петре 1 Гендерные расстройства. Основные понятия
Гендерные расстройства. Основные понятия Деловые бумаги
Деловые бумаги 5 раунд
5 раунд pril1
pril1 Океанариум.
Океанариум. концепция_львы-лисы_мм
концепция_львы-лисы_мм Методика совершенствования технической подготовленности юных конькобежцев с учетом возрастного развития двигательной функции
Методика совершенствования технической подготовленности юных конькобежцев с учетом возрастного развития двигательной функции Филиал кафедры уголовного права и уголовного процесса
Филиал кафедры уголовного права и уголовного процесса Система управления технологическими процессами и информационные технологии в кафе Express pizza
Система управления технологическими процессами и информационные технологии в кафе Express pizza Мое любимое дело - общение с людьми
Мое любимое дело - общение с людьми Автоматизированная диспетчерская служба такси
Автоматизированная диспетчерская служба такси Великие изобретения человечества
Великие изобретения человечества