ПРАВИЛЬНЫЕ МНОГОГРАННИКИ

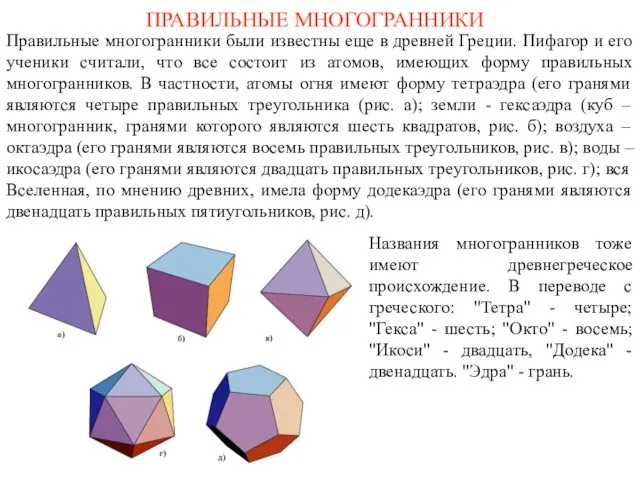
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
Правильные многогранники были известны еще в древней Греции. Пифагор и его ученики считали, что все состоит из атомов, имеющих форму правильных многогранников. В частности, атомы огня имеют форму тетраэдра (его гранями являются четыре правильных треугольника (рис. а); земли - гексаэдра (куб – многогранник, гранями которого являются шесть квадратов, рис. б); воздуха – октаэдра (его гранями являются восемь правильных треугольников, рис. в); воды – икосаэдра (его гранями являются двадцать правильных треугольников, рис. г); вся Вселенная, по мнению древних, имела форму додекаэдра (его гранями являются двенадцать правильных пятиугольников, рис. д).
Названия многогранников тоже имеют древнегреческое происхождение. В переводе с греческого: "Тетра" - четыре; "Гекса" - шесть; "Окто" - восемь; "Икоси" - двадцать, "Додека" - двенадцать. "Эдра" - грань.

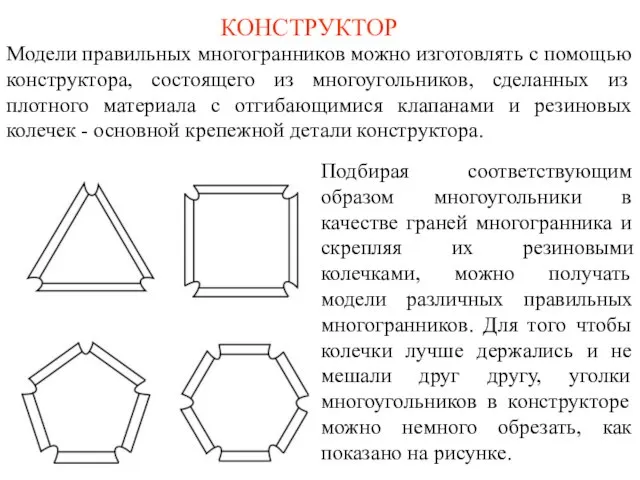
КОНСТРУКТОР
Модели правильных многогранников можно изготовлять с помощью конструктора, состоящего из многоугольников, сделанных из плотного материала с отгибающимися клапанами и резиновых колечек - основной крепежной детали конструктора.
Подбирая соответствующим образом многоугольники в качестве граней многогранника и скрепляя их резиновыми колечками, можно получать модели различных правильных многогранников. Для того чтобы колечки лучше держались и не мешали друг другу, уголки многоугольников в конструкторе можно немного обрезать, как показано на рисунке.

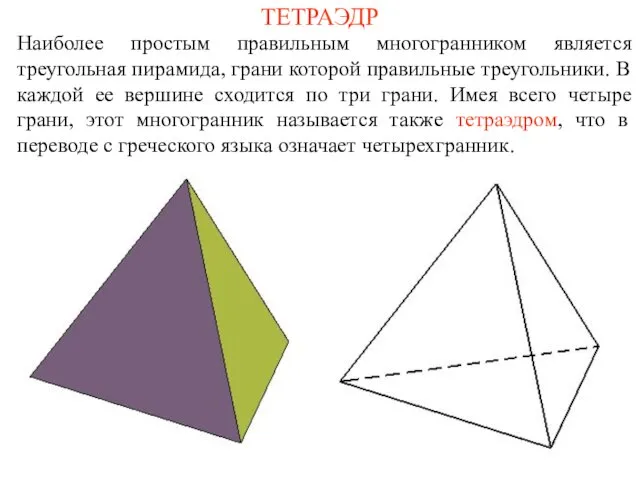
ТЕТРАЭДР
Наиболее простым правильным многогранником является треугольная пирамида, грани которой правильные треугольники. В каждой ее вершине сходится по три грани. Имея всего четыре грани, этот многогранник называется также тетраэдром, что в переводе с греческого языка означает четырехгранник.

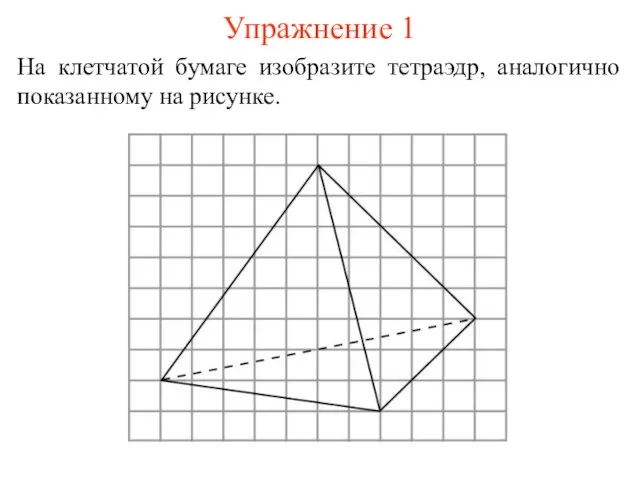
Упражнение 1
На клетчатой бумаге изобразите тетраэдр, аналогично показанному на рисунке.

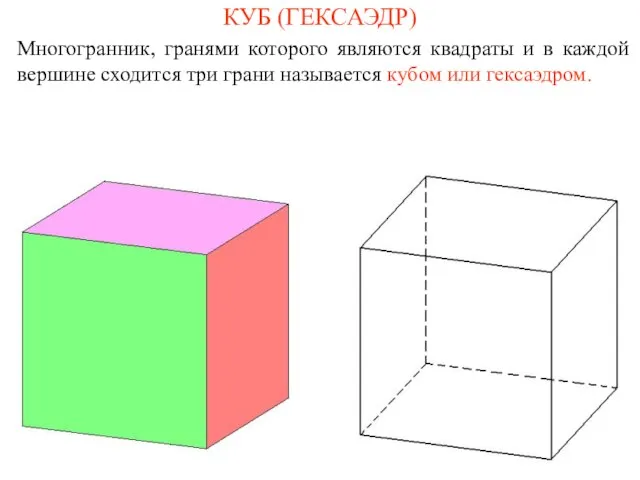
КУБ (ГЕКСАЭДР)
Многогранник, гранями которого являются квадраты и в каждой вершине сходится три грани называется кубом или гексаэдром.

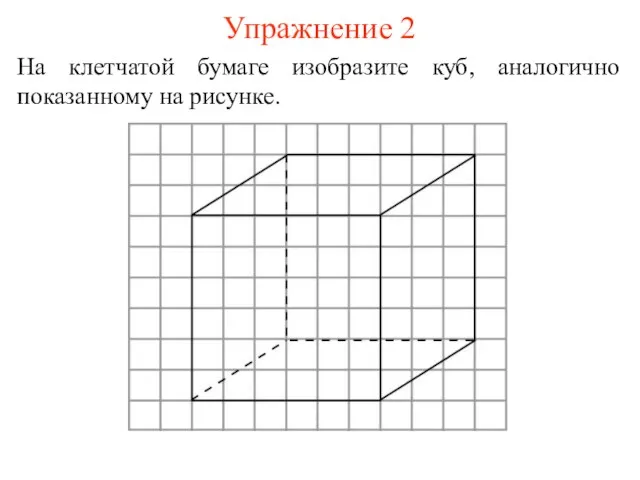
Упражнение 2
На клетчатой бумаге изобразите куб, аналогично показанному на рисунке.

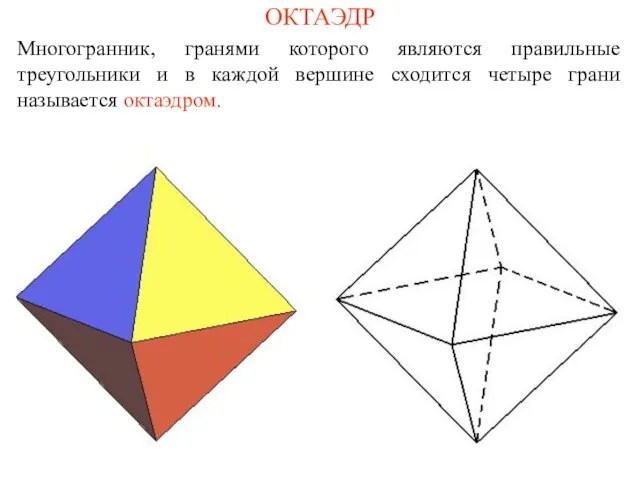
ОКТАЭДР
Многогранник, гранями которого являются правильные треугольники и в каждой вершине сходится четыре грани называется октаэдром.

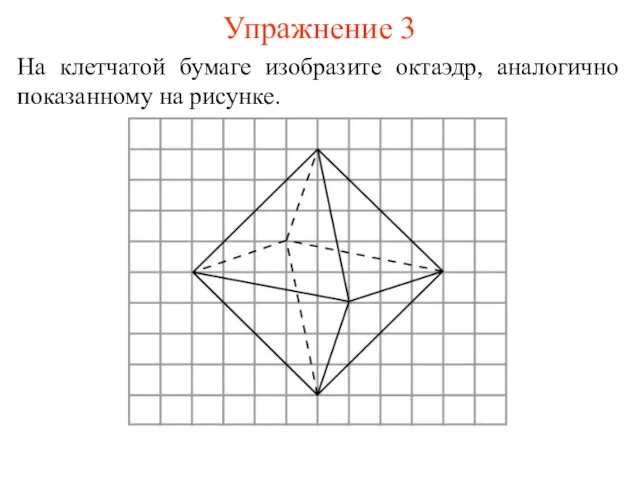
Упражнение 3
На клетчатой бумаге изобразите октаэдр, аналогично показанному на рисунке.

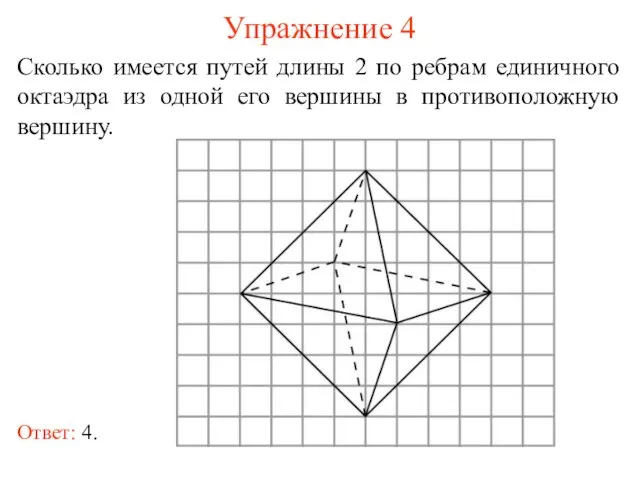
Упражнение 4
Сколько имеется путей длины 2 по ребрам единичного октаэдра из одной его вершины в противоположную вершину.
Ответ: 4.

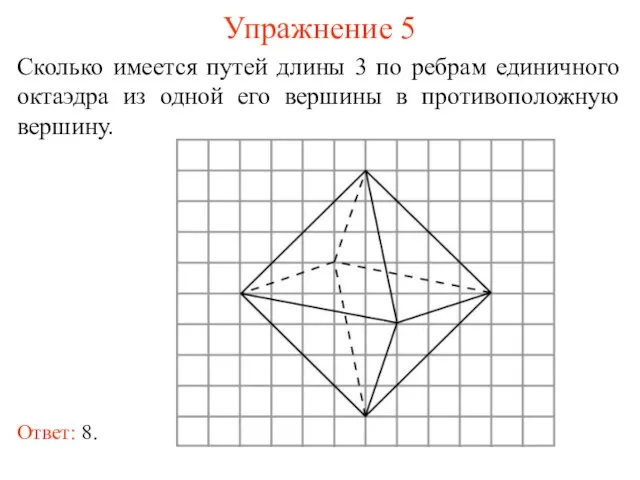
Упражнение 5
Сколько имеется путей длины 3 по ребрам единичного октаэдра из одной его вершины в противоположную вершину.
Ответ: 8.

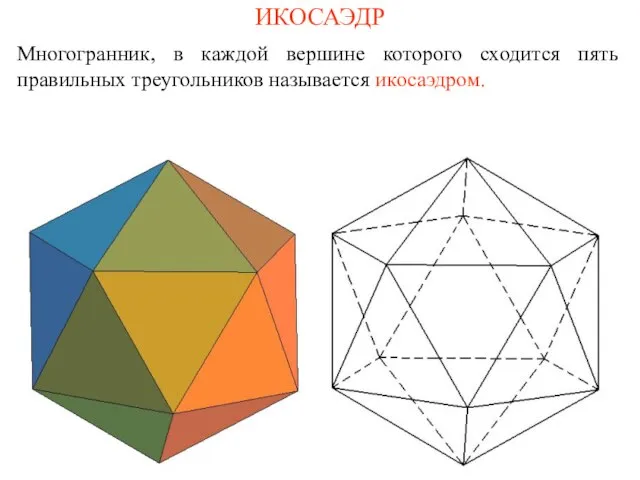
ИКОСАЭДР
Многогранник, в каждой вершине которого сходится пять правильных треугольников называется икосаэдром.

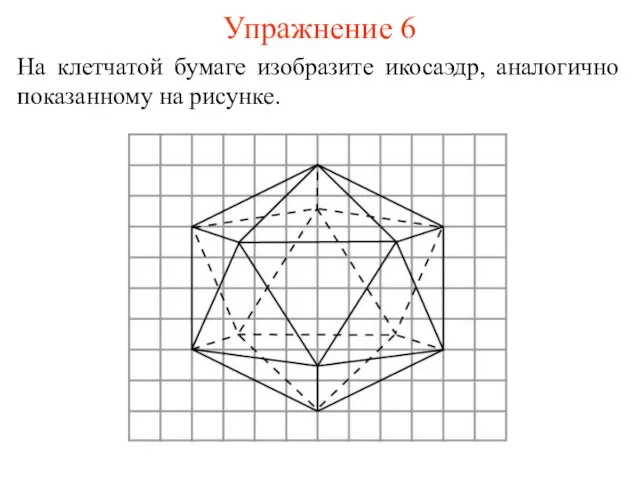
Упражнение 6
На клетчатой бумаге изобразите икосаэдр, аналогично показанному на рисунке.

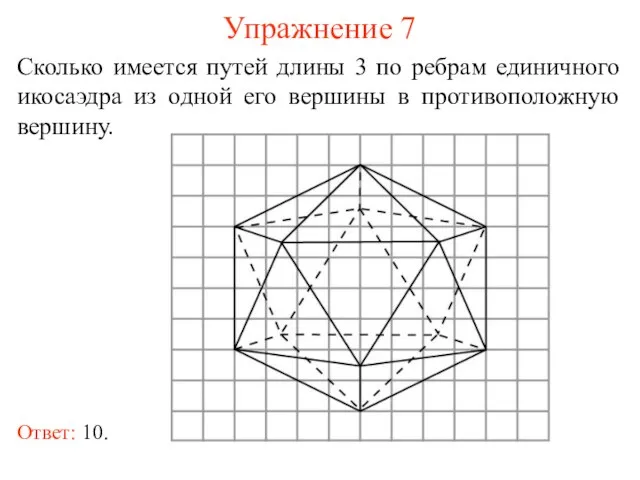
Упражнение 7
Сколько имеется путей длины 3 по ребрам единичного икосаэдра из одной его вершины в противоположную вершину.
Ответ: 10.

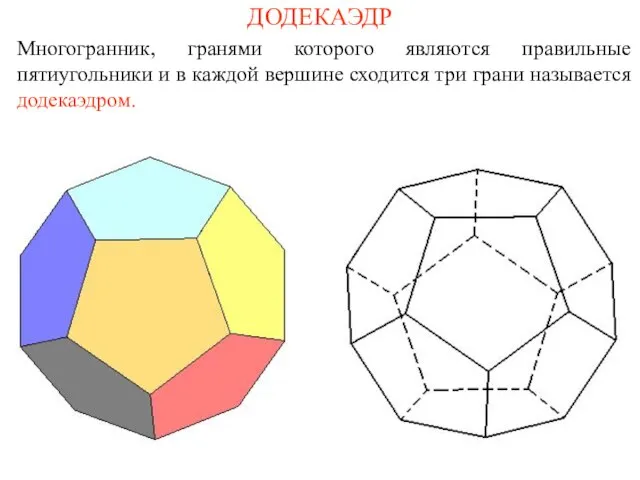
ДОДЕКАЭДР
Многогранник, гранями которого являются правильные пятиугольники и в каждой вершине сходится три грани называется додекаэдром.

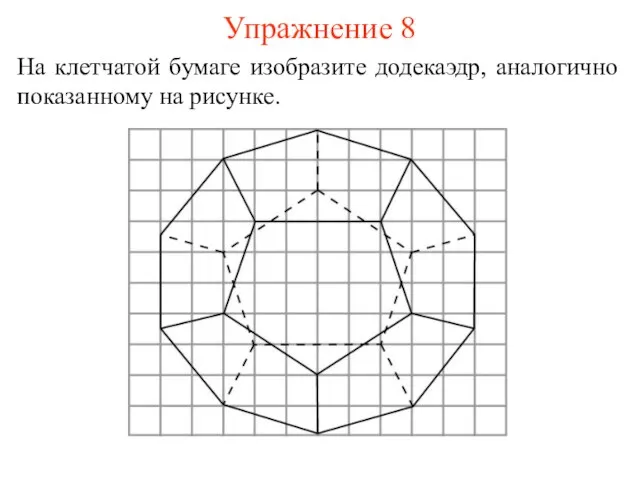
Упражнение 8
На клетчатой бумаге изобразите додекаэдр, аналогично показанному на рисунке.

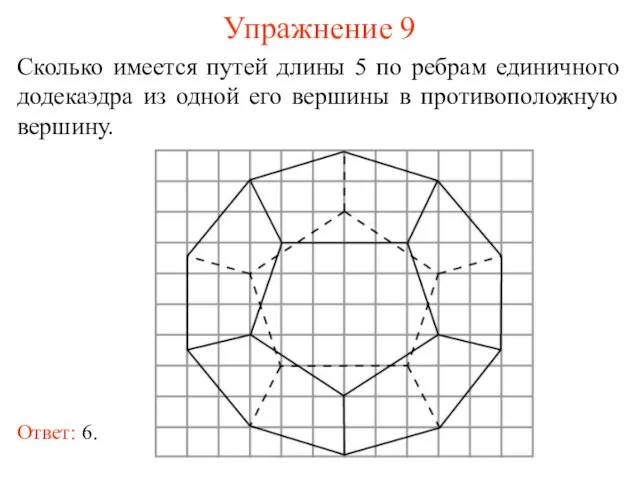
Упражнение 9
Сколько имеется путей длины 5 по ребрам единичного додекаэдра из одной его вершины в противоположную вершину.
Ответ: 6.

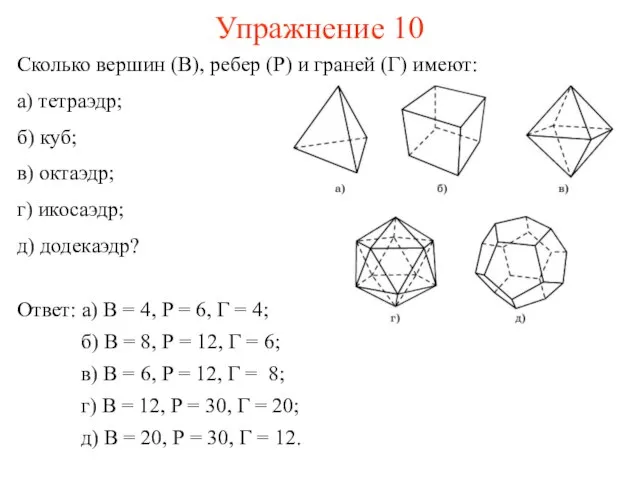
Упражнение 10
Сколько вершин (В), ребер (Р) и граней (Г) имеют:
а) тетраэдр;
б) куб;
в) октаэдр;
г) икосаэдр;
д) додекаэдр?
Ответ: а) В = 4, Р = 6, Г = 4;
б) В = 8, Р = 12, Г = 6;
в) В = 6, Р = 12, Г = 8;
г) В = 12, Р = 30, Г = 20;
д) В = 20, Р = 30, Г = 12.

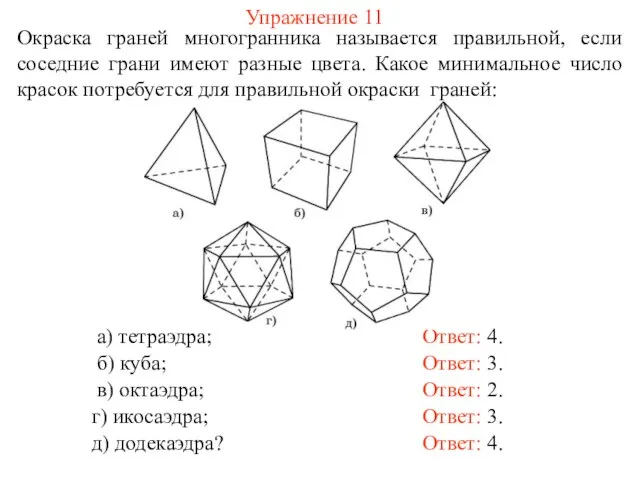
Упражнение 11
Окраска граней многогранника называется правильной, если соседние грани имеют разные цвета. Какое минимальное число красок потребуется для правильной окраски граней:
Ответ: 4.
а) тетраэдра;
б) куба;
в) октаэдра;
г) икосаэдра;
д) додекаэдра?
Ответ: 3.
Ответ: 2.
Ответ: 3.
Ответ: 4.

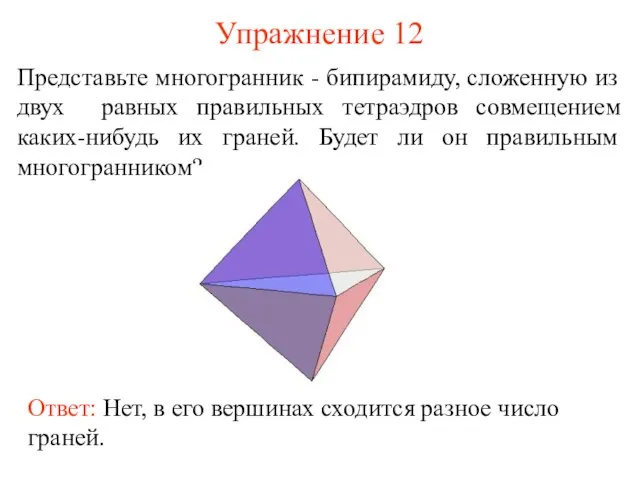
Упражнение 12
Представьте многогранник - бипирамиду, сложенную из двух равных правильных тетраэдров совмещением каких-нибудь их граней. Будет ли он правильным многогранником?
Ответ: Нет, в его вершинах сходится разное число граней.

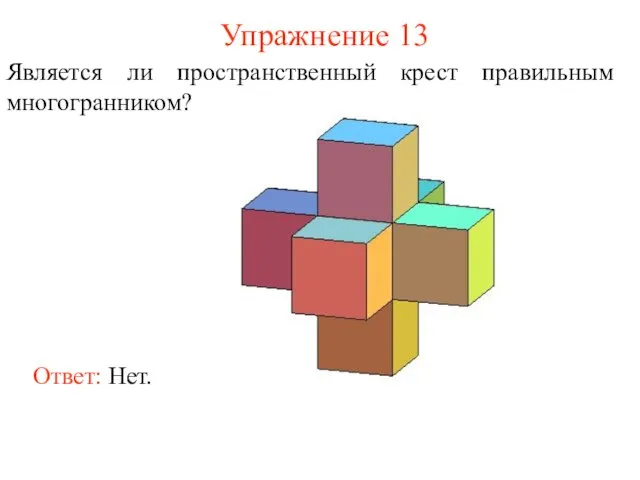
Упражнение 13
Является ли пространственный крест правильным многогранником?
Ответ: Нет.

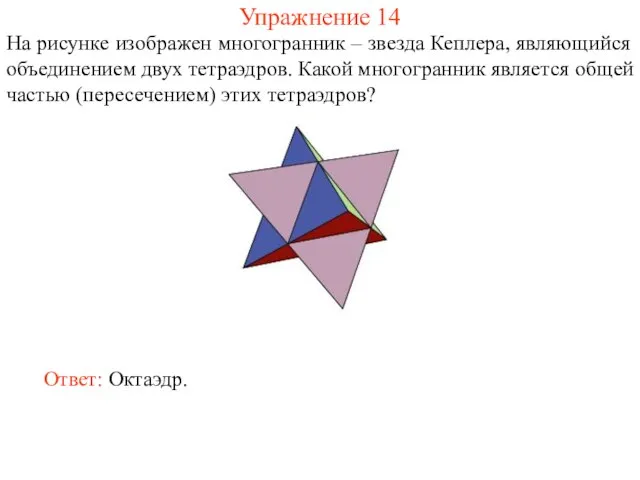
Упражнение 14
На рисунке изображен многогранник – звезда Кеплера, являющийся объединением двух тетраэдров. Какой многогранник является общей частью (пересечением) этих тетраэдров?
Ответ: Октаэдр.

Упражнение 15
Сколько тетраэдров изображено на рисунке?
Ответ: Пять.

Упражнение 16
Сколько кубов изображено на рисунке?
Ответ: Три.

Упражнение 17
Сколько октаэдров изображено на рисунке?
Ответ: Три.

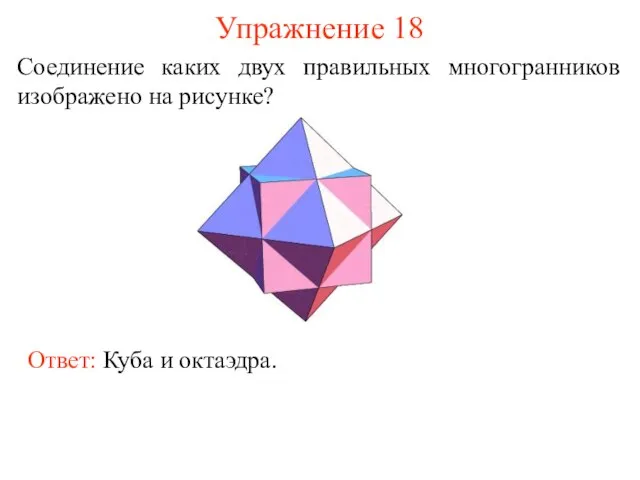
Упражнение 18
Соединение каких двух правильных многогранников изображено на рисунке?
Ответ: Куба и октаэдра.

Упражнение 19
Соединение каких двух правильных многогранников изображено на рисунке?
Ответ: Икосаэдра и додекаэдра.

Упражнение 20
Соединение каких двух правильных многогранников изображено на рисунке?
Ответ: Два икосаэдра.

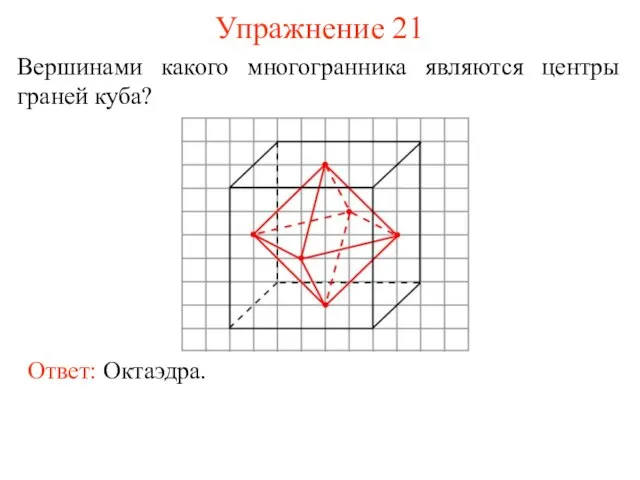
Упражнение 21
Вершинами какого многогранника являются центры граней куба?

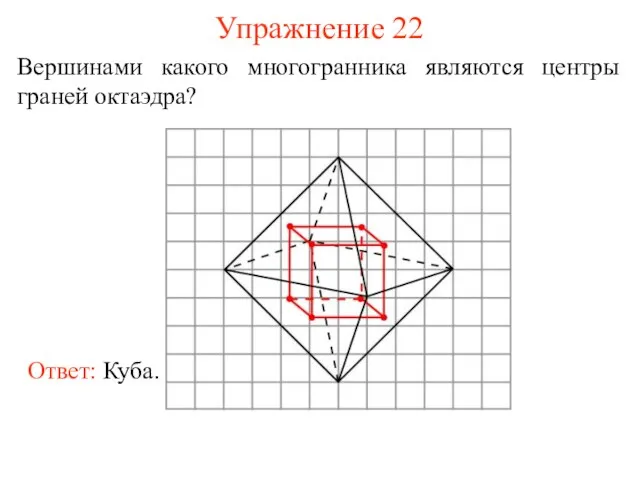
Упражнение 22
Вершинами какого многогранника являются центры граней октаэдра?

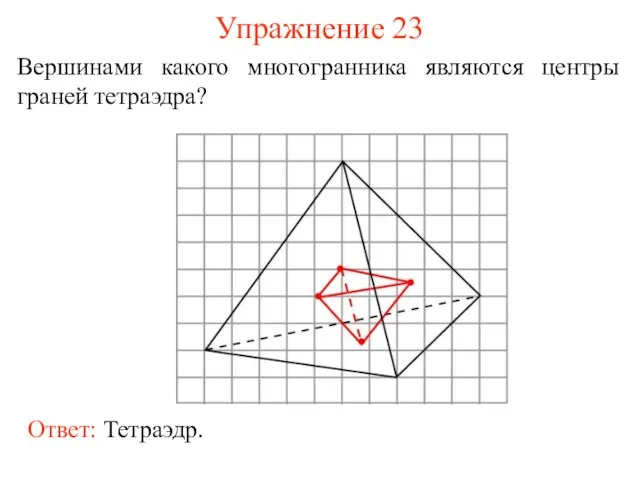
Упражнение 23
Вершинами какого многогранника являются центры граней тетраэдра?

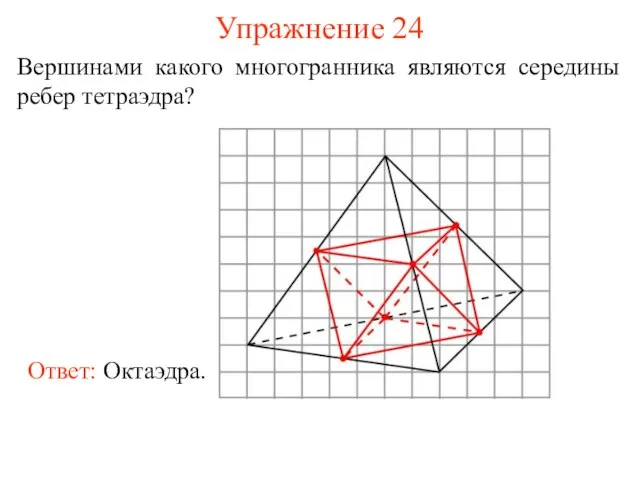
Упражнение 24
Вершинами какого многогранника являются середины ребер тетраэдра?

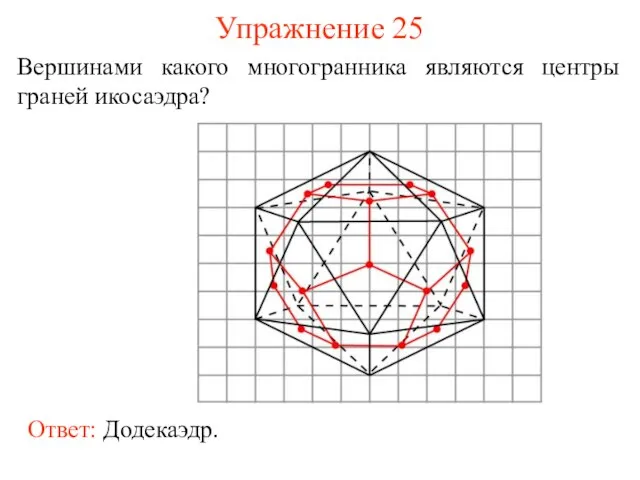
Упражнение 25
Вершинами какого многогранника являются центры граней икосаэдра?

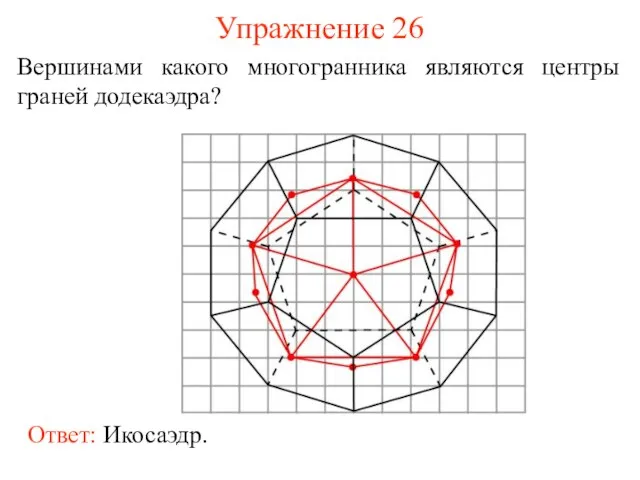
Упражнение 26
Вершинами какого многогранника являются центры граней додекаэдра?

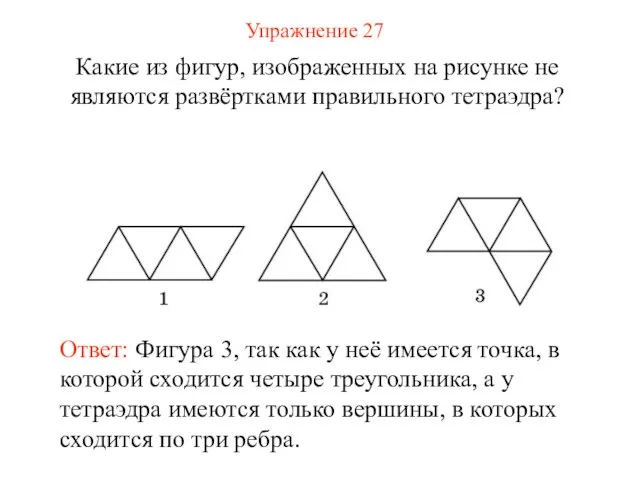
Упражнение 27
Какие из фигур, изображенных на рисунке не являются развёртками правильного тетраэдра?
Ответ: Фигура 3, так как у неё имеется точка, в которой сходится четыре треугольника, а у тетраэдра имеются только вершины, в которых сходится по три ребра.

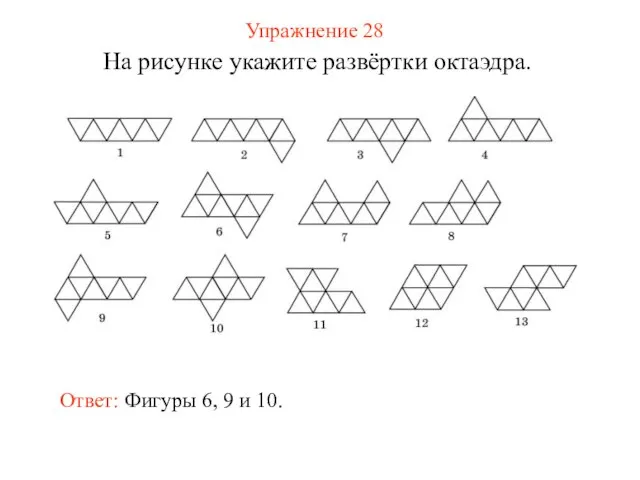
Упражнение 28
На рисунке укажите развёртки октаэдра.
Ответ: Фигуры 6, 9 и 10.

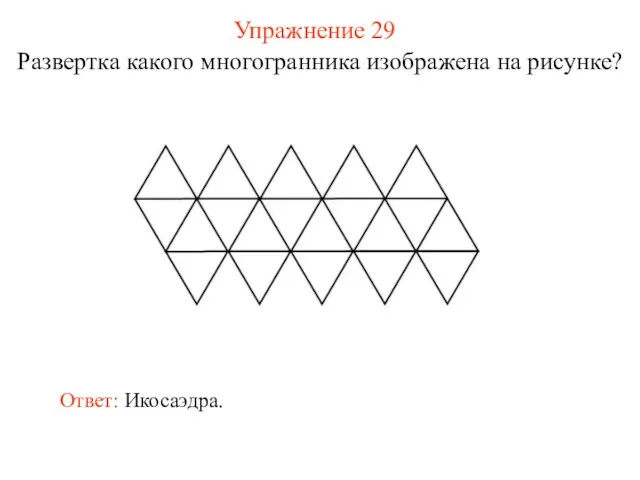
Упражнение 29
Развертка какого многогранника изображена на рисунке?
Ответ: Икосаэдра.

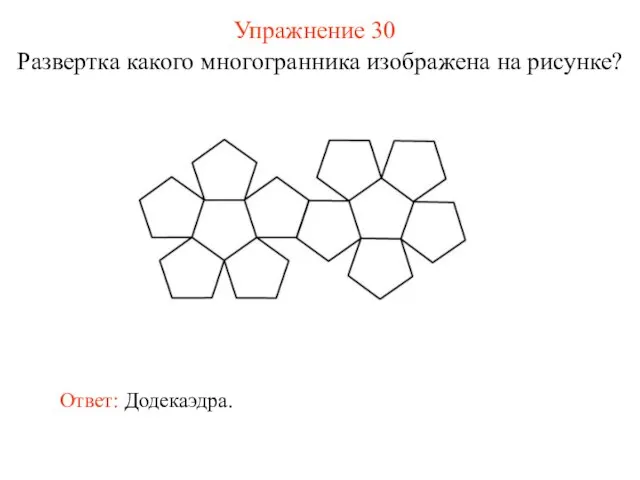
Упражнение 30
Развертка какого многогранника изображена на рисунке?
Ответ: Додекаэдра.

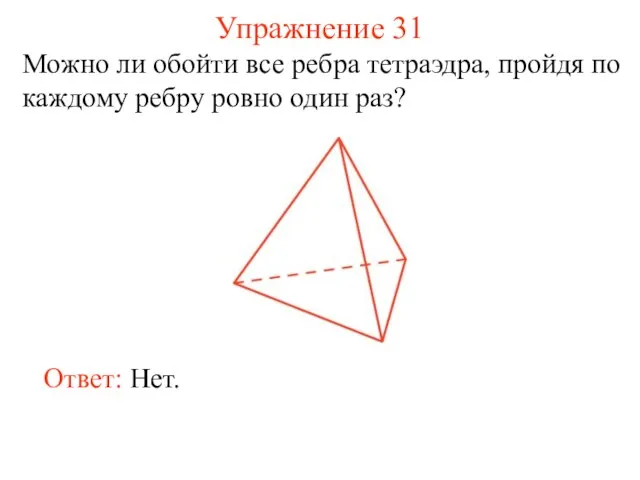
Упражнение 31
Можно ли обойти все ребра тетраэдра, пройдя по каждому ребру ровно один раз?
Ответ: Нет.

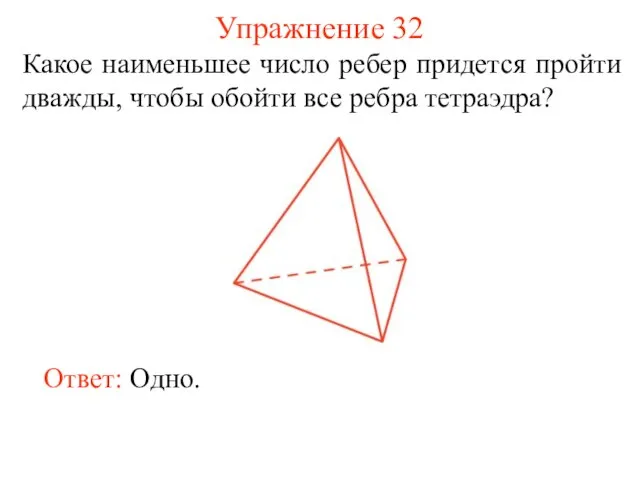
Упражнение 32
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра тетраэдра?
Ответ: Одно.

Упражнение 33
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра тетраэдра и вернуться в исходную вершину?
Ответ: Два.

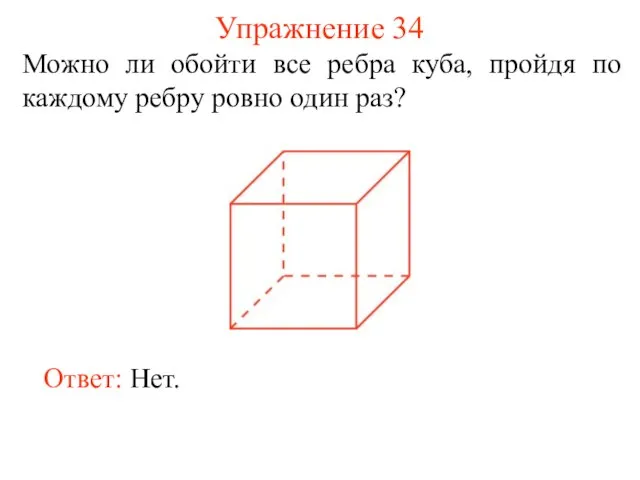
Упражнение 34
Можно ли обойти все ребра куба, пройдя по каждому ребру ровно один раз?
Ответ: Нет.

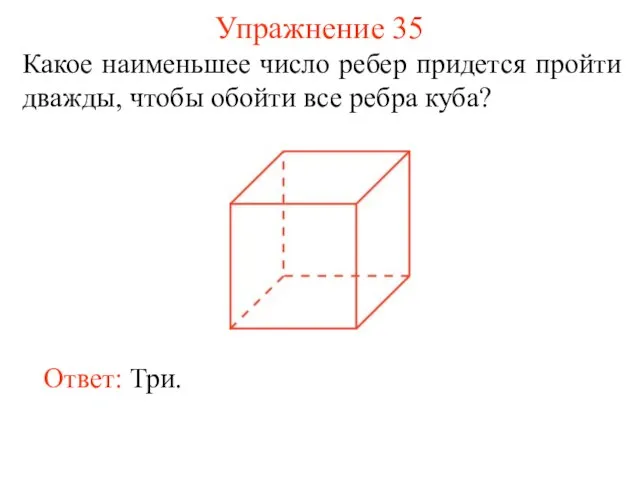
Упражнение 35
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра куба?
Ответ: Три.

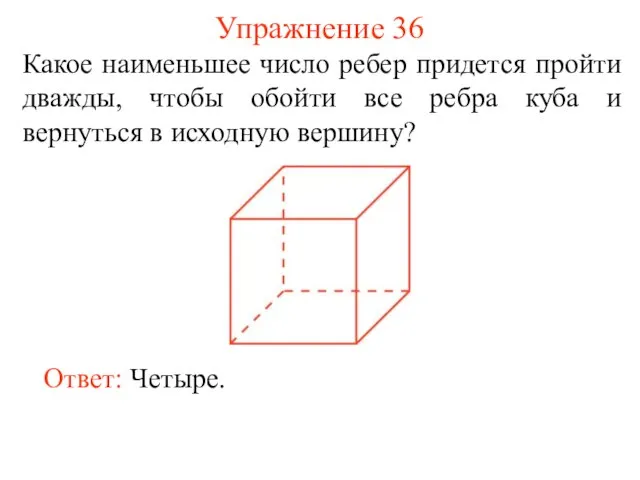
Упражнение 36
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра куба и вернуться в исходную вершину?
Ответ: Четыре.

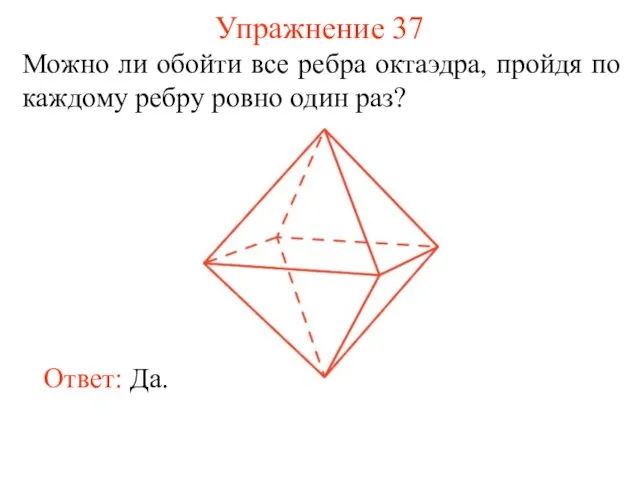
Упражнение 37
Можно ли обойти все ребра октаэдра, пройдя по каждому ребру ровно один раз?
Ответ: Да.

Упражнение 38
Можно ли обойти все ребра икосаэдра, пройдя по каждому ребру ровно один раз?
Ответ: Нет.

Упражнение 39
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра икосаэдра?
Ответ: Пять.

Упражнение 40
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра икосаэдра и вернуться в исходную вершину?
Ответ: Шесть.

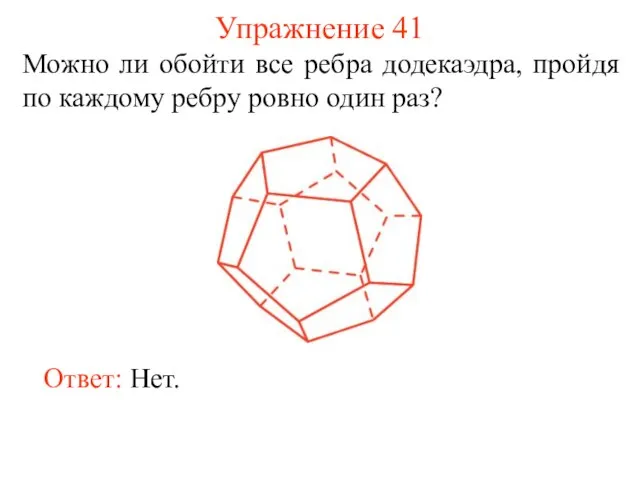
Упражнение 41
Можно ли обойти все ребра додекаэдра, пройдя по каждому ребру ровно один раз?
Ответ: Нет.

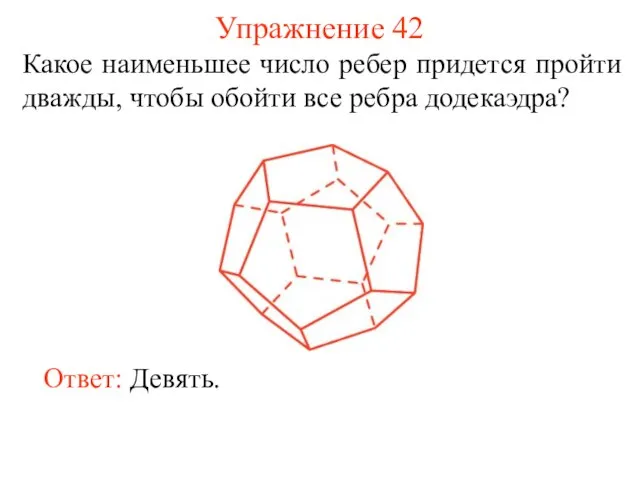
Упражнение 42
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра додекаэдра?
Ответ: Девять.

Упражнение 43
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра додекаэдра и вернуться в исходную вершину?
Ответ: Десять.