Правило умножения Если элемент А можно выбрать m способами, а элемент В можно выбрать n способами, то пару А и В можно выбрать m*n с
Содержание
- 2. Устный счет Вычислить:
- 3. Вычислите:
- 4. Перестановки Размещения Сочетания
- 5. Размещения Размещением элементов из множества Е={а1,...,аn} по k называется упорядоченное подмножество из k элементов, принадлежащих Е.
- 6. Размещение с повторениями Размещение из n элементов множества Е={a1, ..., an} по k - всякая конечная
- 7. Перестановки Перестановки из n элементов - частный случай размещения при k=n. Перестановками называют размещения без повторений
- 8. Сочетания Сочетанием элементов из Е={a1, ..., an} по k называется упорядоченное подмножество из k элементов, принадлежащих
- 9. Простейшие комбинации
- 10. 9.57 В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для
- 11. 9.58 В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать
- 12. 9.62 В классе учатся 16 мальчиков и 12 девочек. Для уборки территории требуется выделить четырех мальчиков
- 13. Задача 1 Сколькими способами могут разместиться 4 пассажира в 4-хместной каюте? 24 4 16
- 14. Задача 2. Четыре человека обменялись рукопожатиями. Сколько было всего рукопожатий? 4 6 8
- 15. Задача 3. Сколько бригад по 3 человек в каждой можно составить из 7 человек для отправки
- 16. Задача 4. Определить число диагоналей 5-тиугольника. 10 5 20
- 17. Задача 5. Сколькими способами могут быть распределены золотая и серебряная медали по итогам олимпиады, если число
- 18. Задача 6. В школьной столовой на обед приготовили в качестве вторых блюд мясо, котлеты и рыбу.
- 19. Задача 7. Трое господ при входе в ресторан отдали швейцару свои шляпы, а при выходе получили
- 20. Проверочная работа 1 вариант 1. Из шести врачей поликлиники двух необходимо отправить на курсы повышения квалификации.
- 22. Скачать презентацию


















 По морям. По волнам
По морям. По волнам Пословицы и поговорки.
Пословицы и поговорки.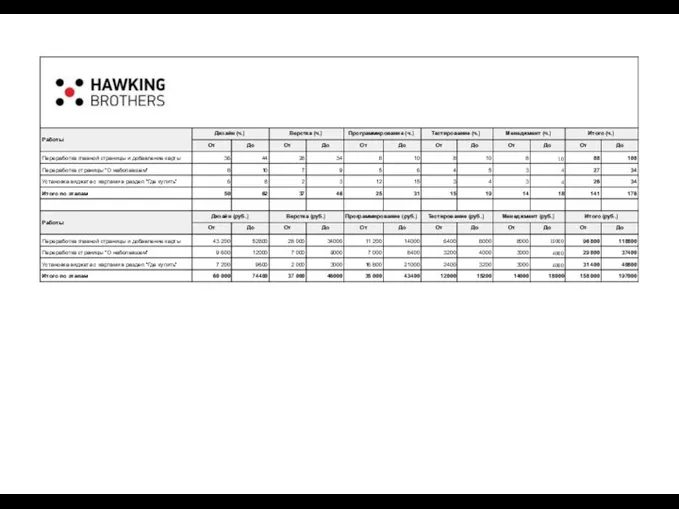 Переработка главной страницы и добавление карты
Переработка главной страницы и добавление карты Критский бык
Критский бык The Great Kremlin Palace
The Great Kremlin Palace  Иван Александрович Гончаров(1812 – 1891)
Иван Александрович Гончаров(1812 – 1891) Формирование адаптивной средычерез использование здоровьесберегающих технологий
Формирование адаптивной средычерез использование здоровьесберегающих технологий Именные библиотеки за рубежом
Именные библиотеки за рубежом Правовые режимы различных категорий земельного фонда
Правовые режимы различных категорий земельного фонда Маркетинговые исследования Исследования в интернете
Маркетинговые исследования Исследования в интернете Почему скисает молоко (4 класс)
Почему скисает молоко (4 класс) Кафедра информационных технологий (КИТ)
Кафедра информационных технологий (КИТ) Платье Feel like a women, wear a dress!
Платье Feel like a women, wear a dress! «1С-Битрикс: Управление сайтом»ПродуктыВозможности сотрудничества
«1С-Битрикс: Управление сайтом»ПродуктыВозможности сотрудничества Всероссийский физкультурно-спортивный комплекс Готов к труду и обороне (ГТО)
Всероссийский физкультурно-спортивный комплекс Готов к труду и обороне (ГТО) канцелярия
канцелярия Акция «Вахта памяти»
Акция «Вахта памяти» Live Краски жизни
Live Краски жизни  Проектная деятельность как форма организации работы с учащимися
Проектная деятельность как форма организации работы с учащимися Кубань – наш общий дом
Кубань – наш общий дом ГУО Сырмежский учебно-педагогический комплекс детский сад – базовая школа
ГУО Сырмежский учебно-педагогический комплекс детский сад – базовая школа Что такое косметика для гурманов? Собрание эксклюзивных средств ISHI из отборного шоколада, высших сортов винограда и редких трюфел
Что такое косметика для гурманов? Собрание эксклюзивных средств ISHI из отборного шоколада, высших сортов винограда и редких трюфел Иванова Нина Борисовна учитель биологии МБОУ «Себежская средняя общеобразователь- ная школа» г.Себеж
Иванова Нина Борисовна учитель биологии МБОУ «Себежская средняя общеобразователь- ная школа» г.Себеж Предложение фирмы «Проектика» по производству и поставке торгового оборудования Рязань 2012 Россия, 390029, г.Рязань, ул.Чкалова, 68А Тел
Предложение фирмы «Проектика» по производству и поставке торгового оборудования Рязань 2012 Россия, 390029, г.Рязань, ул.Чкалова, 68А Тел Управление проектами. Прогнозирование
Управление проектами. Прогнозирование Технологии идентификации
Технологии идентификации Презентация на тему Пожары и взрывы
Презентация на тему Пожары и взрывы немецкое качество российского производства
немецкое качество российского производства