Содержание
- 2. Сила тяжести. Вес Под действием силы притяжения все тела падают на Землю с одинаковым относительно поверхности
- 3. Закон всемирного тяготения Когда великие предшественники Ньютона, в частности Галилей, изучали равноускоренное движение тел, падающих на
- 4. На склоне своих дней Исаак Ньютон рассказал, как это произошло: он гулял по яблоневому саду в
- 5. В «Математических началах натуральной философии» Ньютона есть рисунок под номером 213, замечательный тем, что при всей
- 6. Что случится, если камень бросать все быстрее? Не забудьте, что поверхность Земли кривая. Камень может вылететь
- 7. Ньютон спросил себя: притягивает ли Земля людей так же, как Луну («так же» значит обратно пропорционально
- 8. Желая подтвердить свою теорию тяготения подобными расчетами, Ньютон их аккуратно проделал и... получил сильнейшее несовпадение цифр.
- 9. где G = 6,67∙10–11 Н∙м2/кг2 – гравитационная постоянная. Этот закон справедлив также для сферически симметричных тел
- 10. Относительно этого закона нужно сделать несколько важных замечаний. Во-первых, его действие в явной форме распространяется на
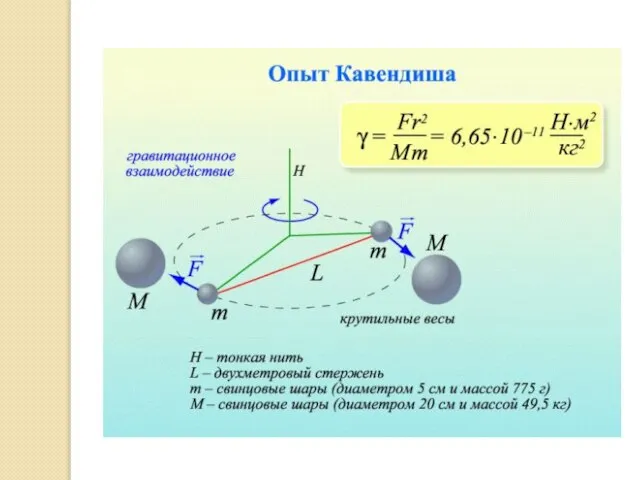
- 11. Опыт Кавендиша Если существует притяжение между любыми двумя объектами, то должна существовать и возможность измерить силу,
- 13. Определив из этого опыта величину G и зная силу притяжения Земли, можно было косвенно определить ее
- 14. Основные труды Кавендиша относятся к химии газов и различным разделам экспериментальной физики. В 1766 г. Кавендиш
- 15. Закон всемирного тяготения был открыт задолго до Исаака Ньютона. К сожалению, всем его открывшим до него
- 16. Вообразите, что могущественное притяжение Солнца почему-либо в самом деле исчезло и Земле предстоит печальная участь навсегда
- 17. И вся эта колоссальная сила проявляется лишь в том, что, искривляя путь движения Земли, каждую секунду
- 18. Ярким примером роли закона всемирного тяготения для науки является история открытия планеты Нептун. В 1781 г.
- 19. Джон Кауч Адамс (1819–1892), британский математик и астроном, внес вклад в теорию движения Луны и рассчитал
- 20. Вид на Нептун с его спутника Тритона
- 21. Что же еще следует из закона тяготения? Наблюдая за спутниками Юпитера, можно понять все законы их
- 22. Причина расхождения оказалась очень естественной и красивой: дело в том, что необходимо какое-то время, чтобы увидеть
- 23. В солнечной системе законы Ньютона абсолютно верны. Но верны ли они на расстояниях, больших, чем относительно
- 24. Сравнивая с «фиксированной» звездой, мы видим, что ось пары повернулась, т. е. звезды ходят одна вокруг
- 25. Здесь показано одно из красивейших небесных зрелищ — шаровые звездные скопления. Каждая точка — это звезда.
- 26. Рассмотрим типичную галактику Форма ее явственно указывает на стремление ее вещества стянуться. Конечно, доказать, что здесь
- 27. Это облака галактик, подобные звездному скоплению. Стало быть, и галактики притягиваются между собой на таких расстояниях,
- 28. Что такое тяготение? Почему закон тяготения так прост? Что можно сказать о причине этого? До сих
- 29. Предлагались многие механизмы тяготения. Интересно рассмотреть один из них, ибо до него время от времени додумывались
- 30. Что же плохо в этом механизме? Неверны те выводы, которые из него следуют. Появляется новая забота:
- 31. Эйнштейн выдвинул доводы, что невозможно посылать сигналы быстрее скорости света; закон тяготения, таким образом, должен быть
- 32. Согласно теории тяготения Эйнштейна в любой конечной области пространство-время окажется искривленным – неевклидовым. Сумма углов треугольника
- 33. «Флатла́ндия» - роман Эдвина Э. Эбботта, который вышел в свет в 1884 году. Этот научно-фантастический роман
- 34. Затем Квадрату снится, что Сфера посещает его снова для того, чтобы представить ему Пойнтландию. Точка (единственный
- 35. В основу ОТО Эйнштейна положены два постулата. Принцип эквивалентности сил инерции и сил гравитации. (Этот факт
- 36. Анализируя этот мысленный эксперимент и тот факт, что любые массы притягиваются всегда, Эйнштейн пришел к мысли,
- 37. И, наконец, сопоставим тяготение с другими теориями. В последние годы выяснилось, что любая масса обязана своим
- 38. Приливы и отливы Под влиянием притяжения Луны и Солнца происходят периодические поднятия и опускания поверхности морей
- 39. Гравитационное воздействие Земли на Луну и наоборот довольно велико. При этом Землю и Луну уже нельзя
- 40. В открытом море подъем водной поверхности во время прилива не превышает 1 м. Значительно большей величины
- 42. В устьях рек приливные волны распространяются вверх по течению, уменьшают скорость течения и могут изменить его
- 44. Благодаря вращению Луны по орбите вокруг Земли между двумя последовательными приливами или двумя отливами в данном
- 46. В наше время приливная энергия в основном превращается в электрическую энергию на приливных электростанциях и вливается
- 48. Скачать презентацию
Слайд 2Сила тяжести. Вес
Под действием силы притяжения все тела падают на Землю с
Сила тяжести. Вес
Под действием силы притяжения все тела падают на Землю с

Это означает, что в системе отсчета, связанной с Землей, на любое тело массы m действует сила
называемая силой тяжести.
Согласно обобщенному закону Галилея, все тела в одном и том же поле тяготения падают с одинаковым ускорением. Следовательно, в данном месте Земли ускорение свободного падения одинаково для всех тел. Оно изменяется вблизи поверхности Земли с широтой в пределах от 9,780 м/с2 на экваторе до 9,832 м/с2 на полюсах. Это обусловлено суточным вращением Земли вокруг своей оси и отличием экваториального и полярного радиусов Земли (соответственно 6378 и 6357 км).
Так как различие значений g невелико, ускорение свободного падения, которое используется при решении практических задач, принимается равным 9,81 м/с2. А Землю принимают за однородный шар радиуса R.
Слайд 3Закон всемирного тяготения
Когда великие предшественники Ньютона, в частности Галилей, изучали равноускоренное движение
Закон всемирного тяготения
Когда великие предшественники Ньютона, в частности Галилей, изучали равноускоренное движение

Когда другие ученые, например Иоганн Кеплер, изучали движение небесных тел, они полагали что в небесных сферах действуют совсем иные законы движения, нежели законы, управляющие движением здесь, на Земле.
Все аргументы, касающиеся движения небесных тел, до Ньютона сводились в основном к тому, что небесные тела, будучи совершенными, движутся по круговым орбитам в силу своего совершенства, поскольку окружность — суть идеальная геометрическая фигура. Таким образом, выражаясь современным языком, считалось, что имеются два типа гравитации, и это представление устойчиво закрепилось в сознании людей того времени. Все считали, что есть земная гравитация, действующая на несовершенной Земле, и есть гравитация небесная, действующая на совершенных небесах.
Слайд 4На склоне своих дней Исаак Ньютон рассказал, как это произошло: он гулял
На склоне своих дней Исаак Ньютон рассказал, как это произошло: он гулял

Поскольку Ньютон в это самое время работал над законами движения он уже знал, что яблоко упало под действием силы тяжести.
Знал он и о том, что Луна не просто висит в небе, а вращается по орбите вокруг Земли, и, следовательно, на нее воздействует какая-то сила, которая удерживает ее от того, чтобы сорваться с орбиты и улететь по прямой прочь, в открытый космос.
Тут ему и пришло в голову, что, возможно, это одна и та же сила заставляет и яблоко падать на землю, и Луну оставаться на околоземной орбите.
Слайд 5В «Математических началах натуральной философии» Ньютона есть рисунок под номером 213, замечательный
В «Математических началах натуральной философии» Ньютона есть рисунок под номером 213, замечательный

Продолжая эти рассуждения, Ньютон приходит к выводу, что если бы не сопротивление воздуха, то по достижении достаточной скорости траектория сделается такой, что камень может вообще никогда не достигнуть поверхности Земли, а станет двигаться вокруг нее, «подобно тому, как планеты описывают в небесном пространстве свои орбиты». Нельзя не вспомнить этой цитаты особенно сейчас, после многочисленных запусков искусственных спутников и космических кораблей.
Слайд 6Что случится, если камень бросать все быстрее? Не забудьте, что поверхность Земли
Что случится, если камень бросать все быстрее? Не забудьте, что поверхность Земли

Может ли такое быть? Да. Хотя камень падает, но и Земля искривляется, вот и получается падение «вокруг» Земли. Надо только узнать, на каком расстоянии поверхность Земли окажется на s=4,9 м ниже горизонта. На рисунке изображена Земля с ее радиусом (R=6370 км) и путь камня (окружность).
Пролетая по горизонтали за 1 секунду расстояние x, камень опускается
на расстояние s. Из подобия треугольников легко получить
x2=(2R-s)s, откуда находим x=7900 м = 7,9 км.
Слайд 7Ньютон спросил себя: притягивает ли Земля людей так же, как Луну («так
Ньютон спросил себя: притягивает ли Земля людей так же, как Луну («так

Можно возразить, что Луна вообще не падает. Но если бы на Луну не действовала сила, она бы унеслась по прямой линии, а на самом деле она обращается по круговой орбите; следовательно, она падает с того места, где она должна была бы быть, если бы сила на нее не действовала.
Зная радиус орбиты Луны (около 384 000 км) и время ее оборота вокруг Земли (около 29 дней), можно подсчитать, сколько она проходит за 1 сек и затем на сколько за это время она падает. Оказывается, что это расстояние примерно равно 1,36 мм. Это хорошо укладывается в закон обратных квадратов, потому что радиус Земли 6370 км, и если на этом расстоянии тела, падая, проходят в первую секунду 4,9 м, то на расстоянии в 384 тыс. км, т. е. в 60 раз дальше от центра Земли, они должны падать на 1/3600 от 4,9 м, или как раз на 1,36 мм.
Слайд 8Желая подтвердить свою теорию тяготения подобными расчетами, Ньютон их аккуратно проделал и...
Желая подтвердить свою теорию тяготения подобными расчетами, Ньютон их аккуратно проделал и...

Шестью годами позже новые измерения радиуса Земли показали, что принятое в ту пору астрономами расстояние до Луны было неверным.
Услышав об этом, Ньютон провел новый расчет с исправленными цифрами и получил уже превосходное совпадение.
Мысль, что Луна «падает», несколько смущает; почему же она тогда не приближается? Эта мысль настолько интересна, что заслуживает дальнейшего пояснения: Луна «падает» в том смысле, что отклоняется от прямой линии, по которой она бы двигалась, не будь больше никаких сил.
Слайд 9где G = 6,67∙10–11 Н∙м2/кг2 – гравитационная постоянная.
Этот закон справедлив также для сферически симметричных
где G = 6,67∙10–11 Н∙м2/кг2 – гравитационная постоянная.
Этот закон справедлив также для сферически симметричных

Слайд 10Относительно этого закона нужно сделать несколько важных замечаний.
Во-первых, его действие в
Относительно этого закона нужно сделать несколько важных замечаний.
Во-первых, его действие в

Во-вторых, ничтожная для небольших масс сила тяготения становится весьма ощутимой, когда речь идет о колоссальных массах небесных тел. Так, даже Нептун, очень далекая от нас планета, медленно кружащаяся почти на краю солнечной системы, шлет нам свой «привет» притяжением Земли с силой 18 миллионов тонн!
Слайд 11Опыт Кавендиша
Если существует притяжение между любыми двумя объектами, то должна существовать и
Опыт Кавендиша
Если существует притяжение между любыми двумя объектами, то должна существовать и

Трудность столь простого по идее опыта заключается в крайней слабости, незаметности сил. Проводить его следует с исключительной осторожностью: сначала выкачать из аппарата воздух, убедиться, что нигде нет электрических зарядов и т. д., и только тогда можно попытаться измерить силу. Впервые она была измерена английским ученым Генри Кавендишем с помощью специальных «крутильных весов».
Опыт доказал, что существует сила, действующая между двумя большими закрепленными свинцовыми шарами и двумя меньшими (тоже из свинца); в опыте шары размещались на концах коромысла, висящего на очень тонкой упругой нити. Измеряя, насколько закрутится нить, можно было узнать величину силы и убедиться, что она обратно пропорциональна квадрату расстояния.
Слайд 13Определив из этого опыта величину G и зная силу притяжения Земли, можно
Определив из этого опыта величину G и зная силу притяжения Земли, можно

Коэффициент G оказался равным
6,670*10-11 ньютон*м2/кг2.
Трудно преувеличить силу влияния теории тяготения, ее величественных успехов на историю науки. Вместо царивших в прежние века неуверенности, сомнений, неполноты знаний, бесконечных споров и парадоксов перед людьми предстал новый закон во всей своей четкости и простоте.
Как важно было то, что все луны, все планеты, все звезды подчиняются столь простому правилу! Но еще важнее то, что человек оказался в состоянии понять это правило и предсказывать на будущее пути планет!
Это определило быстрый, успешный рост науки в последующие годы; у людей появилась надежда, что и в других явлениях мира прячутся такие же простые закономерности.
Слайд 14Основные труды Кавендиша относятся к химии газов и различным разделам экспериментальной физики.
Основные труды Кавендиша относятся к химии газов и различным разделам экспериментальной физики.

В 1781 г. Кавендиш определил состав воздуха, а в 1784 г., сжигая водород, установил химический состав воды, опровергнув представления об её элементарности.
Кавендиш ввёл в науку понятие электрического потенциала, исследовал зависимость ёмкости электрического конденсатора от среды, изучал взаимодействие электрических зарядов, предвосхитив закон Ш. Кулона. Он впервые сформулировал понятие теплоёмкости. В 1790 г. Кавендиш сконструировал крутильные весы и измерил с их помощью силу притяжения двух сфер, подтвердив закон всемирного тяготения, а также определил гравитационную постоянную, массу и среднюю плотность Земли.
Кавендиш Генри(1731 – 1810)
Унаследовав в 1773 г. от своего дяди крупное состояние, Кавендиш тратил почти все доходы на проведение экспериментов; в своем доме в Лондоне он устроил лабораторию, где собрал лучшие приборы и инструменты того времени.
Слайд 15Закон всемирного тяготения был открыт задолго до Исаака Ньютона. К сожалению, всем
Закон всемирного тяготения был открыт задолго до Исаака Ньютона. К сожалению, всем

— Где на земном шаре сила земного тяготения наибольшая?
— В кресле, возле телевизора.
Чем массивней мышцы станут
От зарядок по утрам,
Тем сильнее к ним потянет
Юных девушек и дам.
Физики шутят…
Слайд 16Вообразите, что могущественное притяжение Солнца почему-либо в самом деле исчезло и Земле
Вообразите, что могущественное притяжение Солнца почему-либо в самом деле исчезло и Земле

Вы можете представить себе – здесь необходима фантазия, – что инженеры решили, так сказать, заменить невидимые цепи притяжения материальными связями, т. е. попросту задумали соединить Землю с Солнцем крепкими стальными канатами, которые должны удерживать земной шар на круговом пути в его беге вокруг Солнца.
Представьте себе мощную стальную колонну, поперечником в 5 м. Площадь ее сечения заключает круглым счетом 20 000 000 кв. мм; следовательно, такая колонна разрывается лишь от груза в 2 000 000 тонн. Вообразите далее, что колонна эта простирается от Земли до самого Солнца, соединяя оба светила. Знаете ли вы, сколько таких могучих колонн потребовалось бы для удержания Земли на ее орбите? Миллион миллионов! Чтобы нагляднее представить себе этот лес стальных колонн, густо усеивающих все материки и океаны, прибавлю, что при равномерном распределении их по всей обращенной к Солнцу половине земного шара промежутки между соседними колоннами были бы лишь немногим шире самих колонн.
Слайд 17И вся эта колоссальная сила проявляется лишь в том, что, искривляя путь
И вся эта колоссальная сила проявляется лишь в том, что, искривляя путь

Слайд 18Ярким примером роли закона всемирного тяготения для науки является история открытия планеты
Ярким примером роли закона всемирного тяготения для науки является история открытия планеты

В 1781 г. английский астроном Вильям Гершель открыл планету Уран. Была вычислена ее орбита и составлена таблица положений этой планеты на много лет вперед. Однако проверка этой таблицы показала, что Уран движется не совсем так, как было рассчитано. Ученые предположили, что отклонение в движении Урана вызвано притяжением неизвестной планеты, находящейся от Солнца еще дальше, чем Уран. Зная отклонения от рассчитанной траектории, англичанин Адамс и француз Леверрье, пользуясь законом всемирного тяготения, вычислили положение этой планеты на небе. Адамс раньше закончил вычисления, но наблюдатели, которым он сообщил свои результаты, не торопились с проверкой. А тем временем Леверрье, закончив вычисления, указал немецкому астроному Галле место, где надо искать неизвестную планету.
В первый же вечер, 28 сентября 1846 г., Галле, направив телескоп на указанное место, обнаружил новую планету! Ее назвали Нептуном. Это была первая планета, которую открыли не в ходе наблюдений за небом, а в результате математических вычислений (как говорят, "на кончике пера"). Таким же образом в 1930 году была открыта планета Плутон.
Слайд 19Джон Кауч Адамс (1819–1892), британский математик и астроном, внес вклад в теорию движения
Джон Кауч Адамс (1819–1892), британский математик и астроном, внес вклад в теорию движения

Урбен Леверье (1811–1877), французский математик и астроном, прославился предсказанием о существовании восьмой планеты Нептун и ее положении (независимо от Адамса).
Иоганн Готфрид Галле (1812-1910) немецкий астроном, впервые обнаружил планету Нептун.
Иоганн Готфрид Галле
Слайд 20Вид на Нептун с его спутника Тритона
Вид на Нептун с его спутника Тритона

Слайд 21Что же еще следует из закона тяготения? Наблюдая за спутниками Юпитера, можно
Что же еще следует из закона тяготения? Наблюдая за спутниками Юпитера, можно

Эти спутники очень подробно изучались датским астрономом Рёмером, и вот он заметил, что временами они нарушают расписание: то опаздывают, то приходят в назначенное место раньше времени. Более того, он заметил, что опоздания случаются, когда Юпитер удален от Земли, а когда мы от Юпитера близко, то движение лун опережает расписание.
Такую вещь очень трудно было уложить в закон тяготения, и ему бы угрожала безвременная кончина, не найдись другого объяснения. Ведь если закону противоречит хотя бы один случай, то закон неверен.
Слайд 22Причина расхождения оказалась очень естественной и красивой: дело в том, что необходимо
Причина расхождения оказалась очень естественной и красивой: дело в том, что необходимо
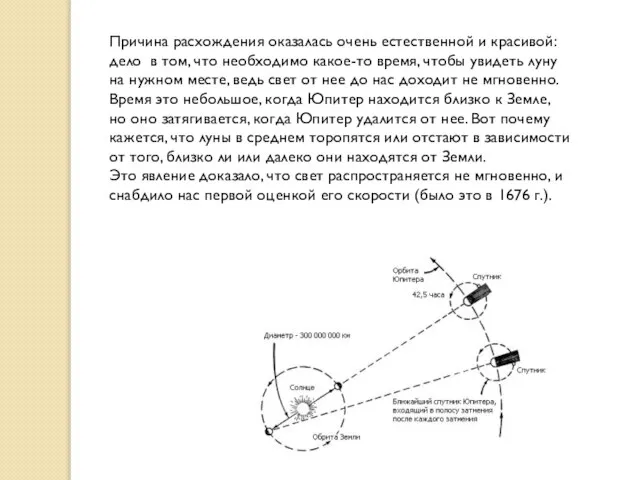
Это явление доказало, что свет распространяется не мгновенно, и снабдило нас первой оценкой его скорости (было это в 1676 г.).
Слайд 23В солнечной системе законы Ньютона абсолютно верны. Но верны ли они на
В солнечной системе законы Ньютона абсолютно верны. Но верны ли они на

Положительные доказательства этого мы находим в двойных звездах. На рисунке показана двойная звезда Сириус— две близкие звезды (третья звезда нужна, чтобы убедиться, что фотография не перевернута); вторая фотография сделана через несколько лет.
Слайд 24Сравнивая с «фиксированной» звездой, мы видим, что ось пары повернулась, т. е.
Сравнивая с «фиксированной» звездой, мы видим, что ось пары повернулась, т. е.

Слайд 25Здесь показано одно из красивейших небесных зрелищ — шаровые звездные скопления. Каждая
Здесь показано одно из красивейших небесных зрелищ — шаровые звездные скопления. Каждая

Больше всего звезд в центре, а по мере удаления к краю их все меньше и меньше. Ясно, что между звездами действует притяжение, т. е. что тяготение существует и на таких гигантских расстояниях .
Слайд 26Рассмотрим типичную галактику
Форма ее явственно указывает на стремление ее вещества стянуться.
Конечно,
Рассмотрим типичную галактику
Форма ее явственно указывает на стремление ее вещества стянуться.
Конечно,

Вы можете сказать: «Ладно, все это разумно, но почему же эта штука, галактика, уже не похожа на шар?» Да потому, что она вертится, что у нее есть момент количества движения (запас вращения); если она сожмется, ей некуда будет его девать; ей остается только сплюснуться.
Слайд 27Это облака галактик, подобные звездному скоплению. Стало быть, и галактики притягиваются между
Это облака галактик, подобные звездному скоплению. Стало быть, и галактики притягиваются между

По-видимому, и на расстояниях в десятки миллионов световых лет проявляется тяготение; насколько ныне известно, всюду все еще действует закон обратных квадратов.
Слайд 28Что такое тяготение?
Почему закон тяготения так прост? Что можно сказать о причине
Что такое тяготение?
Почему закон тяготения так прост? Что можно сказать о причине

Но и никто другой с тех пор никакого механизма не открыл. Все физические законы отличаются в этом отношении своим абстрактным характером. Закон сохранения энергии — это теорема о величинах, которые нужно вычислить и сложить, не думая о причине этого; точно так же и великие законы механики представляют собой количественные математические закономерности, о внутреннем механизме работы которых никаких данных нет.
Почему мы можем пользоваться математикой для описания законов, не зная их причины? Никто и этого не знает. Мы продолжаем идти по этой дороге, потому что на ней все еще происходят открытия.
Слайд 29Предлагались многие механизмы тяготения. Интересно рассмотреть один из них, ибо до него
Предлагались многие механизмы тяготения. Интересно рассмотреть один из них, ибо до него

каждый сперва воспрянет духом и ходит осчастливленный
своим «открытием», но потом начинает понимать, что тут что-то не так.
Впервые это «открытие» произошло примерно в 1750 г. Представьте себе, что в пространстве носится в разных направлениях с огромной скоростью множество частиц, лишь слегка поглощаемых веществом. Поглощаясь, они передают свой импульс Земле. Но так как во всех направлениях их количество одинаково, то все импульсы уравновешиваются. Когда же неподалеку находится Солнце, то частицы, приближающиеся к Земле сквозь Солнце, частично им поглощаются, так что от Солнца их проходит меньше, чем с обратной стороны. Следовательно, Земля ощутит импульс, направленный к Солнцу, и нетрудно показать, что он будет обратным квадрату расстояния: таков закон изменения пространственного угла, под которым видимо Солнце, с ростом расстояния.
Слайд 30Что же плохо в этом механизме?
Неверны те выводы, которые из него
Что же плохо в этом механизме?
Неверны те выводы, которые из него

Так и не было предложено ни одного механизма, «объясняющего» тяготение, который бы не предсказывал добавочных, несуществующих явлений.
Однако, несмотря на вызванное им воодушевление, ньютонов закон тяготения все же неверен!
Учтя требования теории относительности, Эйнштейн видоизменил этот закон. Согласно Ньютону, тяготение действовало мгновенно. Это значит вот что: сдвинув массу, мы должны в тот же миг почувствовать изменение силы в результате смещения; стало быть, таким способом можно посылать сигналы с бесконечной скоростью.
Слайд 31Эйнштейн выдвинул доводы, что невозможно посылать сигналы быстрее скорости света; закон тяготения,
Эйнштейн выдвинул доводы, что невозможно посылать сигналы быстрее скорости света; закон тяготения,

E=mc2.
Поэтому он должен тяготеть к другим объектам. Даже световой луч имеет «массу», ибо он обладает энергией. И когда луч света, неся с собой энергию, проходит мимо Солнца, то Солнце его притягивает. И луч уже идет не по прямой, а искривляется. Например, во время солнечных затмений звезды, окружающие Солнце, кажутся сдвинутыми с того места, где они наблюдались бы, если бы Солнца не было. И это явление и впрямь наблюдалось!
Слайд 32Согласно теории тяготения Эйнштейна в любой конечной области пространство-время окажется искривленным –
Согласно теории тяготения Эйнштейна в любой конечной области пространство-время окажется искривленным –

Согласно Эйнштейну, истинное гравитационное поле есть проявление искривления четырехмерного пространства-времени. Кривизна пространства-времени создается источниками гравитационного поля – массами вещества и всеми видами энергии, присутствующими в системе, поскольку энергия и масса эквивалентны.
Тяготение зависит не только от распределения масс в пространстве, но и от их движения, давления и напряжений, имеющихся в телах от всех физических полей. Движение тел в искривленном пространстве-времени происходит по кратчайшим траекториям – геодезическим, которые в трехмерном пространстве-времени воспринимаются как движение по искривленным траекториям с переменной скоростью. Изменение гравитационных полей в вакууме распространяется со скоростью света.
Слайд 33«Флатла́ндия» - роман Эдвина Э. Эбботта, который вышел в свет в 1884
«Флатла́ндия» - роман Эдвина Э. Эбботта, который вышел в свет в 1884

Действие романа происходит в двумерном мире под названием Флатландия. Безымянный рассказчик, скромный квадрат (социальная группа джентльменов во Флатландии), показывает читателю различные сферы жизни в двух измерениях. Квадрат видит сон о посещении одномерного мира (Лайнландии), и пытается доказать невежественному монарху Лайнландии существование второго измерения, но находит, что невозможно вынудить его посмотреть за пределы своей вечно прямой линии.
Затем рассказчика посещает трёхмерная сфера, суть которой он не может постигнуть.
Слайд 34Затем Квадрату снится, что Сфера посещает его снова для того, чтобы представить
Затем Квадрату снится, что Сфера посещает его снова для того, чтобы представить

Квадрат признаёт связь между невежеством монархов Пойнтландии и Лайнландии со своим собственным предыдущим невежеством при отрицании существования других измерений. Когда Квадрат вернулся во Флатландию, он нашёл невероятно трудным убедить кого-либо в том, что существует Трёхмерное Пространство, особенно после того, как официальные лица заявили, что любой, кто станет проповедовать «ложь трёх измерений», будет пожизненно заключён в тюрьму.
В конечном счёте, Квадрата сажают в тюрьму именно по этой причине, откуда он и ведёт повествование.
Слайд 35В основу ОТО Эйнштейна положены два постулата.
Принцип эквивалентности сил инерции и
В основу ОТО Эйнштейна положены два постулата.
Принцип эквивалентности сил инерции и
Гравитационное взаимодействие распространяется с конечной скоростью, равной скорости света с в виде гравитационных волн. (Пока кванты гравитационного поля – гравитоны – не обнаружены).
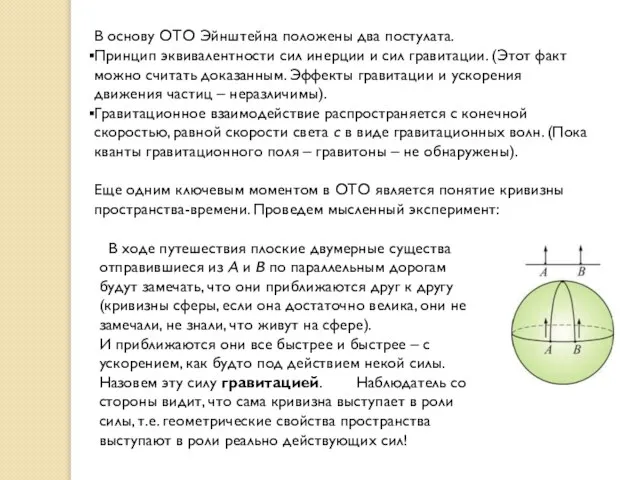
Еще одним ключевым моментом в ОТО является понятие кривизны пространства-времени. Проведем мысленный эксперимент:
В ходе путешествия плоские двумерные существа отправившиеся из А и В по параллельным дорогам будут замечать, что они приближаются друг к другу (кривизны сферы, если она достаточно велика, они не замечали, не знали, что живут на сфере).
И приближаются они все быстрее и быстрее – с ускорением, как будто под действием некой силы. Назовем эту силу гравитацией. Наблюдатель со стороны видит, что сама кривизна выступает в роли силы, т.е. геометрические свойства пространства выступают в роли реально действующих сил!
Слайд 36Анализируя этот мысленный эксперимент и тот факт, что любые массы притягиваются всегда,
Анализируя этот мысленный эксперимент и тот факт, что любые массы притягиваются всегда,

Слайд 37И, наконец, сопоставим тяготение с другими теориями. В последние годы выяснилось, что
И, наконец, сопоставим тяготение с другими теориями. В последние годы выяснилось, что

Квантовомеханические стороны природы мы еще пока не распространили на тяготение. Когда на малых расстояниях начинаются квантовые эффекты, то тяготение оказывается еще настолько слабым, что нужды в квантовой теории тяготения не возникает.
С другой стороны, для последовательности наших физических теорий было бы важно понять, должен ли закон Ньютона с внесенным Эйнштейном видоизменением быть изменен и дальше с тем, чтобы согласовываться с принципом неопределенности. Это последнее видоизменение пока не сделано.
Слайд 38Приливы и отливы
Под влиянием притяжения Луны и Солнца происходят периодические поднятия и
Приливы и отливы
Под влиянием притяжения Луны и Солнца происходят периодические поднятия и

Наибольшие приливы наблюдаются в дни сизигий (новолуний и полнолуний), наименьшие (квадратурные) совпадают с первой и последней четвертями Луны. Между сизигиями и квадратурами амплитуды приливов могут изменяться в 2,7 раза.
Лунные приливы в 2,17 раза превышают по силе солнечные.
Слайд 39Гравитационное воздействие Земли на Луну и наоборот довольно велико. При этом Землю
Гравитационное воздействие Земли на Луну и наоборот довольно велико. При этом Землю
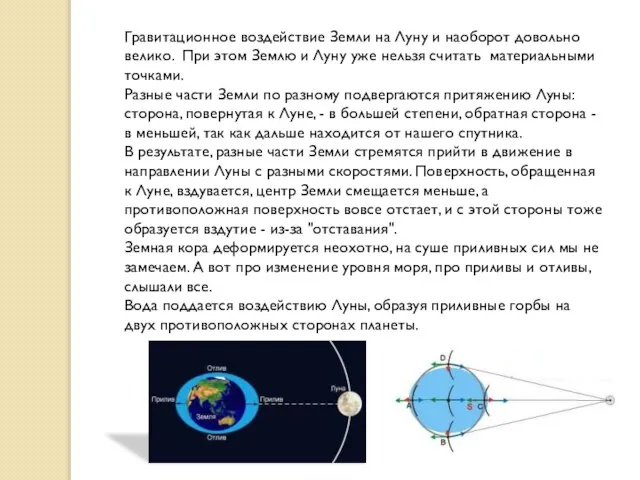
Разные части Земли по разному подвергаются притяжению Луны: сторона, повернутая к Луне, - в большей степени, обратная сторона - в меньшей, так как дальше находится от нашего спутника.
В результате, разные части Земли стремятся прийти в движение в направлении Луны с разными скоростями. Поверхность, обращенная к Луне, вздувается, центр Земли смещается меньше, а противоположная поверхность вовсе отстает, и с этой стороны тоже образуется вздутие - из-за "отставания".
Земная кора деформируется неохотно, на суше приливных сил мы не замечаем. А вот про изменение уровня моря, про приливы и отливы, слышали все.
Вода поддается воздействию Луны, образуя приливные горбы на двух противоположных сторонах планеты.
Слайд 40В открытом море подъем водной поверхности во время прилива не превышает 1
В открытом море подъем водной поверхности во время прилива не превышает 1

При отливах на пологих берегах морей может происходить обнажение дна на расстоянии в несколько километров по перпендикуляру к береговой линии. Рыбаки Терского побережья Белого моря и полуострова Новая Шотландия в Канаде используют это обстоятельство при ловле рыбы. Перед приливом они устанавливают на пологом берегу сети, а после спада воды подъезжают к сетям на телегах и собирают попавшую в чих рыбу.
Слайд 42В устьях рек приливные волны распространяются вверх по течению, уменьшают скорость течения
В устьях рек приливные волны распространяются вверх по течению, уменьшают скорость течения

На некоторых реках (Северн и Трент в Англии, Сена и Орне во Франции, Амазонка в Бразилии) приливное течение создает крутую волну высотой 2...5 м, которая распространяется вверх по реке со скоростью 7 м/сек. За первой волной может следовать несколько волн меньших размеров. По мере продвижения вверх волны постепенно ослабевают, при встрече с отмелями и преградами они с шумом дробятся и пенятся.
Река Сен-Джонс в Канаде, недалеко от места впадения в залив Фанди, проходит через узкое ущелье. Во время прилива ущелье задерживает движение воды вверх по реке, уровень воды выше ущелья оказывается ниже и поэтому образуется водопад с движением воды против течения реки. При отливе же вода не успевает достаточно быстро проходить через ущелье в обратном направлении, поэтому уровень воды выше ущелья оказывается выше и образуется водопад, через который вода устремляется вниз по течению реки.
Слайд 44Благодаря вращению Луны по орбите вокруг Земли между двумя последовательными приливами или
Благодаря вращению Луны по орбите вокруг Земли между двумя последовательными приливами или

Вследствие суточного вращения Земли и движения Земли, Луны и Солнца по своим орбитам, приливообразующая сила в каждой точке на поверхности Земли непрерывно меняется во времени, никогда точно не повторяясь. Однако приливные силы можно представить как сумму большого числа строго периодических составляющих, определяемых из теории движения Луны вокруг Земли и Земли вокруг Солнца.
Вращаясь, Земля "подставляет" Луне разные свои стороны, и приливной горб перемещается по поверхности. Такие деформации земной коры вызывают внутреннее трение, которое тормозит вращение нашей планеты. Раньше она вращалась гораздо быстрее. Луна еще больше подвергнута влиянию приливных сил, ведь Земля гораздо массивнее. Скорость вращения Луны настолько замедлилась, что она повернулась к нашей планете одной стороной, и приливной горб не бежит более по лунной поверхности.
Слайд 46В наше время приливная энергия в основном превращается в электрическую энергию на
В наше время приливная энергия в основном превращается в электрическую энергию на

В Кислой губе вблизи Мурманска с 1968 года начала работать первая в нашей стране приливная электростанция мощностью в 400 киловатт. Проектируется приливная электростанция в устье Мезени и Кулоя мощностью 2,2 млн киловатт.
За рубежом разрабатываются проекты приливных электростанций в заливе Фанди (Канада) и в устье реки Северн (Англия) мощностью соответственно в 4 и 10 млн киловатт, вступили в строй приливные электростанции Ранс и Сен-Мало (Франция) мощностью в 240 и 9 тыс. киловатт, работают небольшие приливные электростанции в Китае.
Поскольку запасы приливной энергии планеты значительно превосходят полную величину гидроэнергии рек, можно полагать, что приливная энергия будет играть заметную роль в дальнейшем прогрессе человеческого общества.



 Методы и формы работы в программе дополнительного образования
Методы и формы работы в программе дополнительного образования Синдром одержимости
Синдром одержимости Лек 3 харак кулин продукции
Лек 3 харак кулин продукции Символизм и модерн как стилистические направления начала XX века
Символизм и модерн как стилистические направления начала XX века Бухгалтерская (финансовая) отчетность. Отчет об изменениях капитала. Лекция 5
Бухгалтерская (финансовая) отчетность. Отчет об изменениях капитала. Лекция 5 Поддержка стандарта OpenGIS в СУБД ЛИНТЕР
Поддержка стандарта OpenGIS в СУБД ЛИНТЕР № 1 Введение в дисциплину
№ 1 Введение в дисциплину Как сохранить здоровье ребенка? 7 класс
Как сохранить здоровье ребенка? 7 класс Warp Knitted Safety Jacket Fabric
Warp Knitted Safety Jacket Fabric Родительское собраниепо теме"Школа-дом-одна семья"
Родительское собраниепо теме"Школа-дом-одна семья" ТЕМА: ОБОРУДОВАНИЕ ДЛЯ ПРИЕМКИ ПРОДУКЦИИ
ТЕМА: ОБОРУДОВАНИЕ ДЛЯ ПРИЕМКИ ПРОДУКЦИИ Ledeco – профессиональный партнер в сфере реализации инженерно-строительных проектов
Ledeco – профессиональный партнер в сфере реализации инженерно-строительных проектов Тест по экономике
Тест по экономике МОУ Лицей №74
МОУ Лицей №74 Разработка модели управления Разработка модели управленияпроцессом полоролевого воспитания детей дошкольного и младшего шк
Разработка модели управления Разработка модели управленияпроцессом полоролевого воспитания детей дошкольного и младшего шк Проверочная работа по теме: «Функциональное устройство компьютера» (Запишите на листочках свои имя и фамилию,номер варианта и за
Проверочная работа по теме: «Функциональное устройство компьютера» (Запишите на листочках свои имя и фамилию,номер варианта и за Итоги проведения конкурсных процедур и приемки государственных контрактов, выполненных в рамках ФЦПРО на 2011-2015 годы в 2011 году
Итоги проведения конкурсных процедур и приемки государственных контрактов, выполненных в рамках ФЦПРО на 2011-2015 годы в 2011 году Способы разделения смесей
Способы разделения смесей Характерные черты информационного общества
Характерные черты информационного общества Школьная профилактически - образовательная программа «УРОКИ ЗДОРОВЬЯ»
Школьная профилактически - образовательная программа «УРОКИ ЗДОРОВЬЯ» Инклюзивное образование
Инклюзивное образование ВНИМАНИЕ!!!
ВНИМАНИЕ!!! Повторение изученного по фонетике и орфоэпии
Повторение изученного по фонетике и орфоэпии OKD_chistaya_linia
OKD_chistaya_linia Культура через призму психоанализа: Фрейд, Юнг, Фромм
Культура через призму психоанализа: Фрейд, Юнг, Фромм Поручение Президента РФ
Поручение Президента РФ Презентация на тему Money деньги
Презентация на тему Money деньги  Украинцы в Красноярском крае
Украинцы в Красноярском крае