Презентация на тему Двугранный угол

геометрическая фигура, состоящая из двух полуплоскостей с общей границей, не развернутых в одну плоскость
DABC
DBCA
DACB
CADB
CDBA
ADCB
ребро
грани
KDBA
KDBC
двугранных углов нет

сечение двугранного угла плоскостью, перпендикулярной ребру
от выбора точки С на ребре (почему?)
градусная мера соответствующего линейного угла
Найти ( увидеть) ребро и грани двугранного угла
В гранях найти направления ( прямые) перпендикулярные ребру
(при необходимости) заменить выбранные направления параллельными им лучами с общим началом на ребре двугранного угла
параллельность и отношение длин параллельных отрезков

АС
АСР
АСВ
и
В грани АСВ
В грани АСР
угол РСВ - линейный для двугранного угла с ребром АС
АСВ
прямая СВ перпендикулярна ребру СА ( по условию)
прямая СР перпендикулярна ребру СА
( по теореме о трех перпендикулярах)

АС
АСР
и
АСВ
В грани АСВ
К
В грани АСР
угол РКВ - линейный для двугранного угла с РСАВ
прямая ВО перпендикулярна ребру СА
( по свойству равностороннего треугольника)
прямая РК перпендикулярна ребру СА
( по теореме о трех перпендикулярах)

а). Двугранный угол РТМК:
(2) В грани МТР
В грани МТК
А
В
С
(1) ребро МТ, грани МТР и МТК
прямая ТР перпендикулярна ребру МТ
( по определению прямой, перпендикулярной плоскости)
прямая МК перпендикулярна ребру МТ
( по условию)

а). Двугранный угол РТМК:
А
В
С
АВ параллельна РТ (по построению), а так как РТ перпендикулярна ребру МТ ( по доказанному), то АВ перпендикулярна ребру МТ (по лемме о связи параллельности и перпендикулярности)
Аналогично ВС перпендикулярна ребру МТ
Значит, угол АВС – искомый

б). Двугранный угол РМКТ:
В грани МКР
(2) В грани МТК
Ответ. Угол РМТ - линейный для двугранного угла с РМКТ
(1) ребро МК, грани МКР и МКТ
прямая МТ перпендикулярна ребру МК ( по условию)
прямая МР перпендикулярна ребру МК
( по теореме о трех перпендикулярах)

в). Двугранный угол РТКМ:
В грани КРТ
(2) В грани МТК
(1) ребро ТК, грани ТКМ и ТКР
прямая МХ, где Х – середина КТ, перпендикулярна ребру КТ ( по свойству равнобедренного треугольника)
прямая РТ перпендикулярна ребру КТ
( по определению прямой перпендикулярной плоскости)

в). Двугранный угол РТКМ:
(3) Построим прямую УХ параллельно прямой РТ , она будет лежать в
плоскости РКТ (почему?),
получим , что прямая ХУ перпендикулярно ребру КТ
(по лемме о связи параллельности и перпендикулярности
Значит, искомый угол УХМ

Пример вычислительной задачи по теме «Двугранный угол»

Для тех, кто недостаточно хорошо справился с задачами урока, предлагается
необязательное домашнее задание:
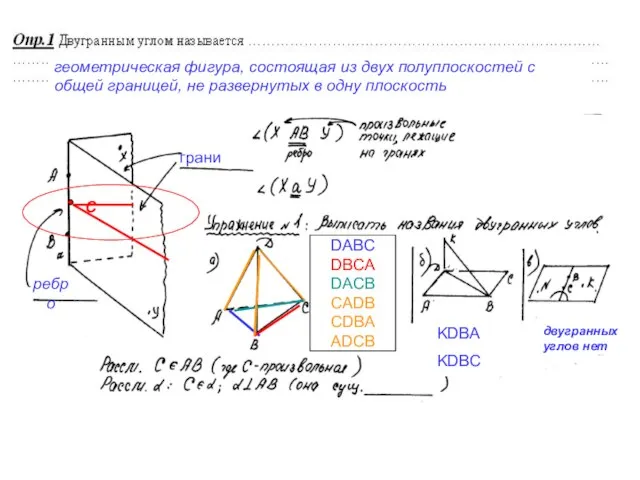
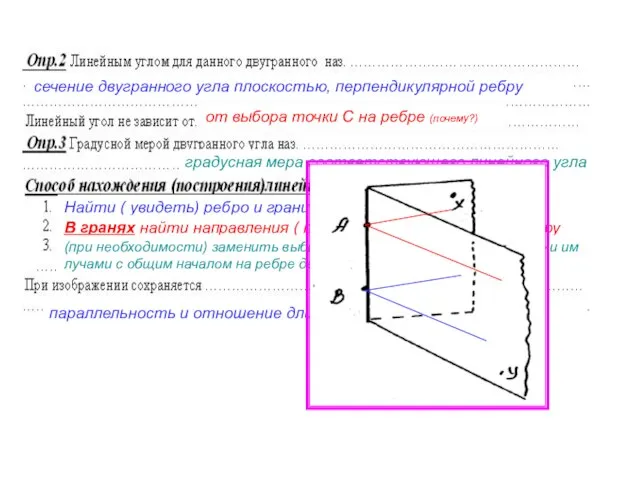
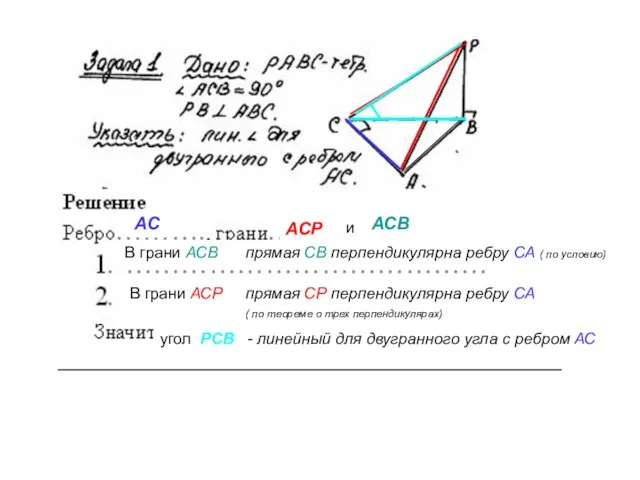
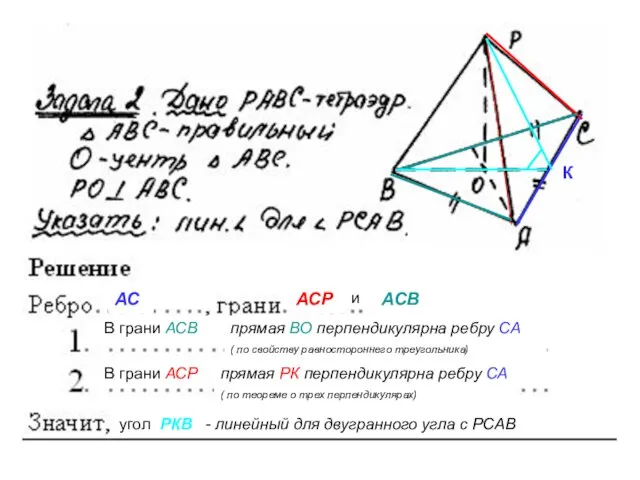
Сделать модели к зачетным задачам №1-4 ( см. стр.2-4 конспекта), изменив названия вершин и положение тетраэдра, но не меняя отличительных черт задачи: например, в задаче №1 в основании тетраэдра должен лежать прямоугольный равнобедренный треугольник, а вершина должна проектироваться в одну из вершин острого угла основания. К модели приложить запись решения задачи. Модель может быть как объемной, так и складной. Своей моделью можно будет пользоваться на зачете.
2. Оформить решение задачи, аналогичной разобранной зачетной задачи №1, в виде презентации.
3. Придумать несколько задач, аналогичных зачетным задачам №1 и №2, и оформить каждую из них по образцу на стр.2-3 конспекта. Каждая страница оценивается максимальным баллом 1. Нормы оценок по количеству сданных страниц.
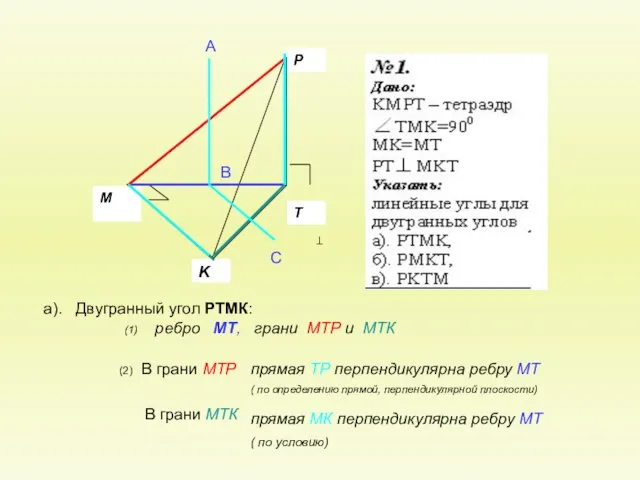
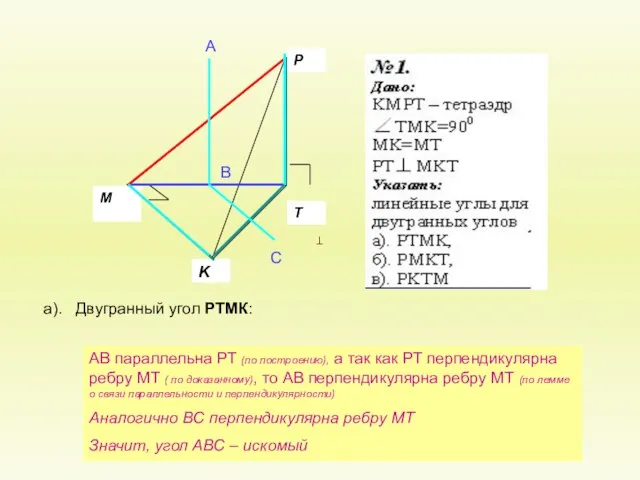
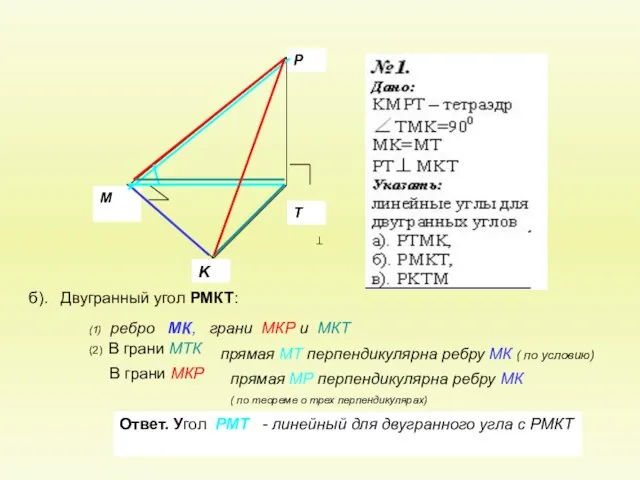
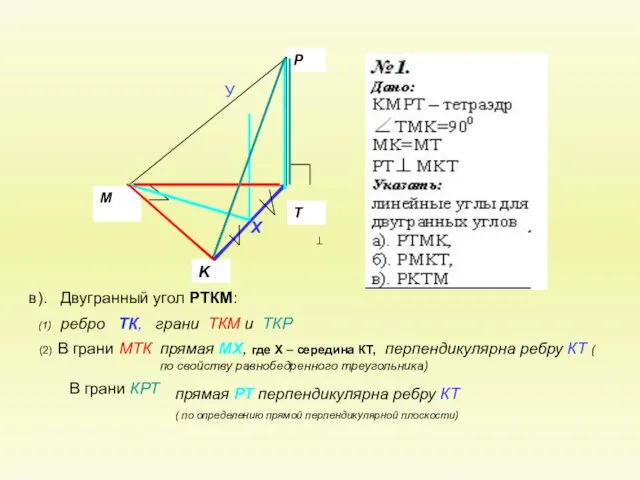
Геометрия 10. тема « Двугранный угол»