Содержание
- 2. Цели урока Ввести определение компланарных векторов. Рассмотреть признак компланарности трех векторов и правило параллелепипеда, сложение трех
- 3. Новый материал Определение. Векторы называются компланарными, если при откладывании от одной и той же точки они
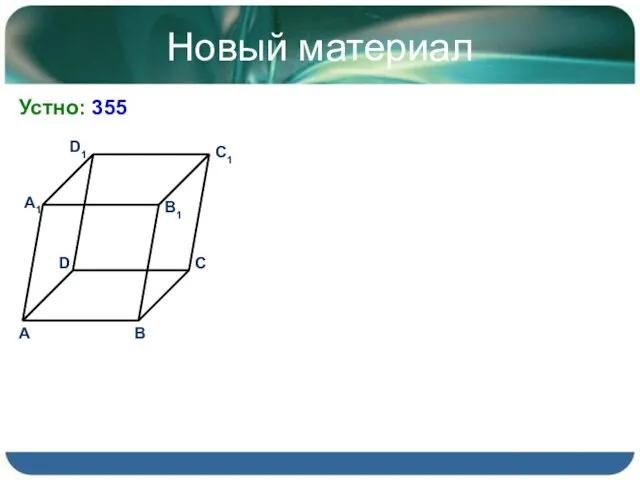
- 4. Новый материал Устно: 355
- 5. Новый материал Признак компланарности трех векторов:
- 6. Новый материал Признак компланарности трех векторов: • О А1 В1 С
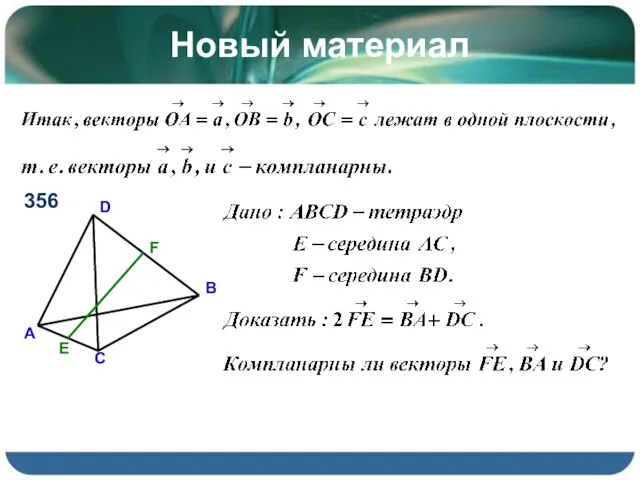
- 7. Новый материал 356
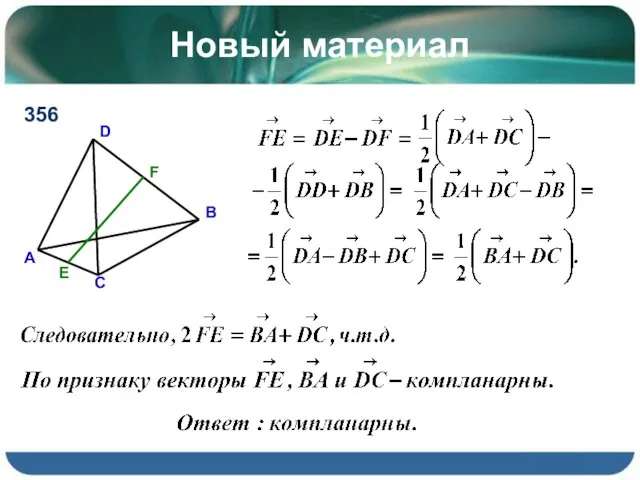
- 8. Новый материал 356
- 9. Новый материал Определение. Утверждение, обратное признаку компланарности векторов: Докажем это.
- 10. Новый материал О А В Р Р1 Так как векторы компланарны, то они лежат в одной
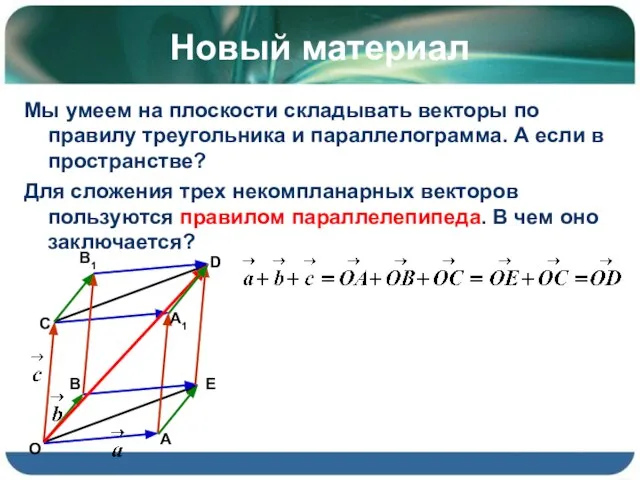
- 11. Новый материал Мы умеем на плоскости складывать векторы по правилу треугольника и параллелограмма. А если в
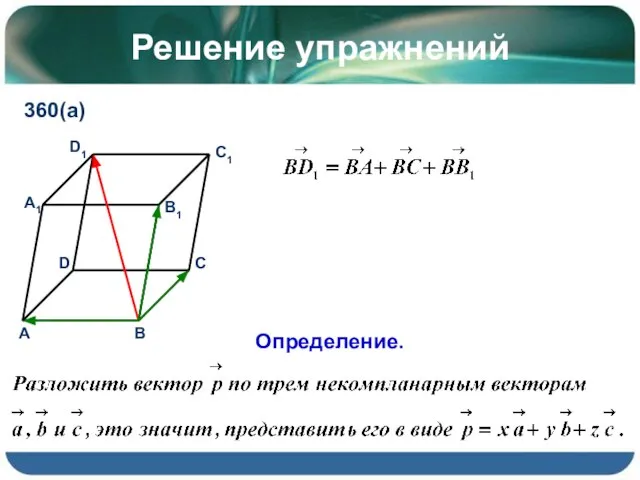
- 12. Решение упражнений 360(а) Определение.
- 13. Домашнее задание п. 39, 40 вопросы 13-15 стр. 97 358, 360(б), 368(а, б)
- 15. Скачать презентацию







 Жудожник. Эссе
Жудожник. Эссе COMP 875 Machine Learning Methods in Image Analysis
COMP 875 Machine Learning Methods in Image Analysis Патохарактерологический диагностический опросник
Патохарактерологический диагностический опросник 6.5. Импульсный фотометр ФИ-1
6.5. Импульсный фотометр ФИ-1 Презентация на тему Правильные и полуправильные многогранники
Презентация на тему Правильные и полуправильные многогранники -Н- и –НН- в прилагательных и причастиях Автор: учитель русского языка и литературы МОУ «СОШ р.п.Духовницкое» Куч
-Н- и –НН- в прилагательных и причастиях Автор: учитель русского языка и литературы МОУ «СОШ р.п.Духовницкое» Куч Авторы: Корочкина Лариса Владимировна, Корочкин Виктор Сергеевич МОУ «СОШ № 7» г. Муром Владимирская область
Авторы: Корочкина Лариса Владимировна, Корочкин Виктор Сергеевич МОУ «СОШ № 7» г. Муром Владимирская область Цель
Цель Использование местных сырьевых ресурсов в сельскохозяйственном производстве ИННОВАЦИОННЫЙ ПРОЕКТ Комплекс получения энергии из
Использование местных сырьевых ресурсов в сельскохозяйственном производстве ИННОВАЦИОННЫЙ ПРОЕКТ Комплекс получения энергии из Проблемы пресечения злоупотребления налоговыми правами в сфере взимания налога на доходы физических лиц
Проблемы пресечения злоупотребления налоговыми правами в сфере взимания налога на доходы физических лиц 20141029_testovye_tekhnologii_v_fgos
20141029_testovye_tekhnologii_v_fgos Шоколад
Шоколад Введение в Data Mining
Введение в Data Mining Немецкие автомобили
Немецкие автомобили  Юлия Друнина: Я родом не из детства – Нет, это не заслуга, а удача — из войны
Юлия Друнина: Я родом не из детства – Нет, это не заслуга, а удача — из войны Перепечи из пестиков
Перепечи из пестиков Всё видео Интернета на Ваших телевизорах!ViNTERA – Интернет-ТВ приставка
Всё видео Интернета на Ваших телевизорах!ViNTERA – Интернет-ТВ приставка Презентация на тему Из Саратова с любовью (From Saratov with love)
Презентация на тему Из Саратова с любовью (From Saratov with love)  Применение свойств функций к решению уравнений и неравенств
Применение свойств функций к решению уравнений и неравенств Обобщение и систематизация знаний по теме «Подгруппа углерода».
Обобщение и систематизация знаний по теме «Подгруппа углерода». Картина-портрет
Картина-портрет «Обнаружитель людейпри катастрофах»
«Обнаружитель людейпри катастрофах» Анализ памятника архитектуры. Замок Кршивоклат. Чехия
Анализ памятника архитектуры. Замок Кршивоклат. Чехия Трение. Вредно или полезно
Трение. Вредно или полезно Стивен Джордж Таллентс
Стивен Джордж Таллентс Основные рекомендации к разработке и проведению здоровьесберегающего урока
Основные рекомендации к разработке и проведению здоровьесберегающего урока Сливки сухие растительные Биокрим
Сливки сухие растительные Биокрим Секреты общения
Секреты общения