Презентация на тему Функции у=sin x и y = cos x и их графики

ОПРЕДЕЛЕНИЕ
Числовые функции, заданные формулами
у=sin x и y = cos x, называют соответственно синусом и косинусом.
10.11.2013
КОРПУСОВА Т.С.

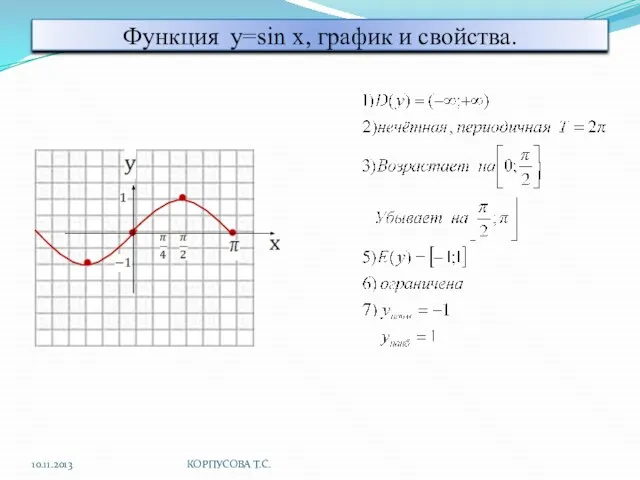
Функция y=sin x, график и свойства.
10.11.2013
КОРПУСОВА Т.С.

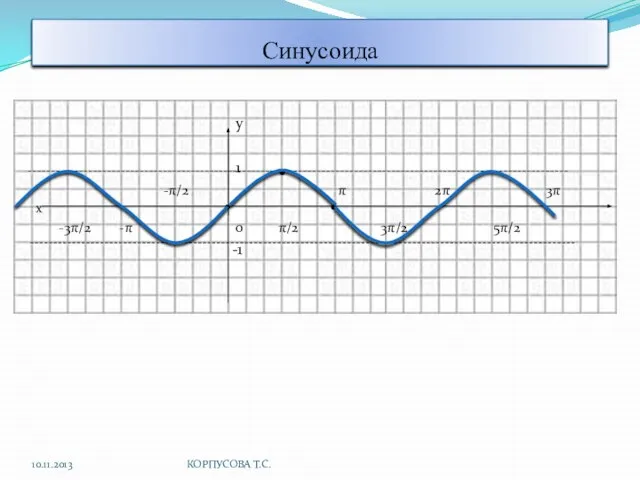
Синусоида
у
1
-π/2 π 2π 3π х
-3π/2 -π 0 π/2 3π/2 5π/2
-1
10.11.2013
КОРПУСОВА Т.С.

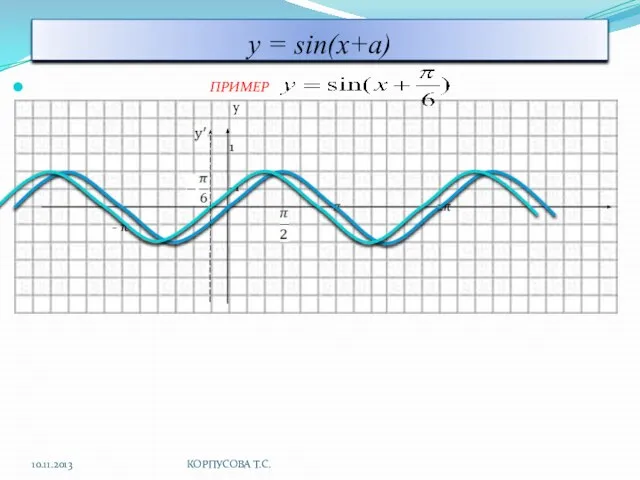
у = sin(x+a)
ПРИМЕР
y
1
-1
π 2π
- π
10.11.2013
КОРПУСОВА Т.С.

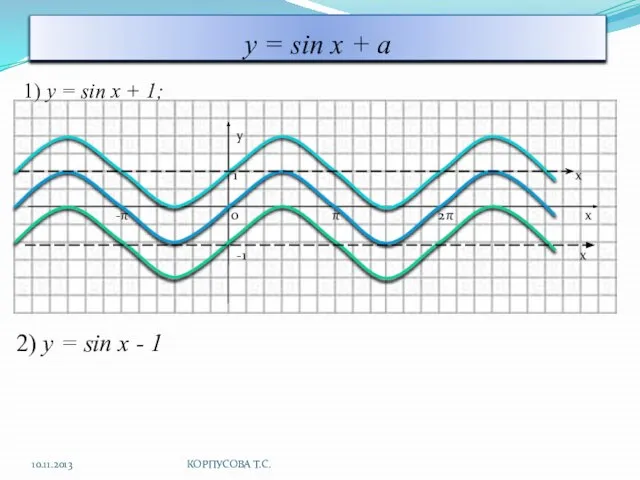
у = sin x + a
1) y = sin x + 1;
y
1 x
-π 0 π 2π x
-1 x
2) y = sin x - 1
10.11.2013
КОРПУСОВА Т.С.

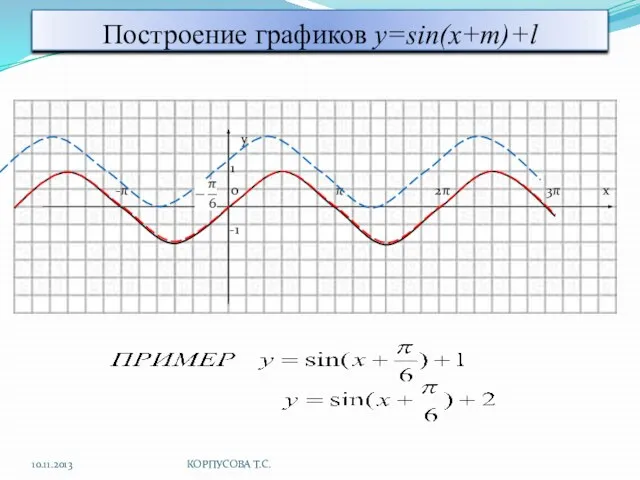
Построение графиков y=sin(x+m)+l
y
1
-π 0 π 2π 3π x -1
10.11.2013
КОРПУСОВА Т.С.

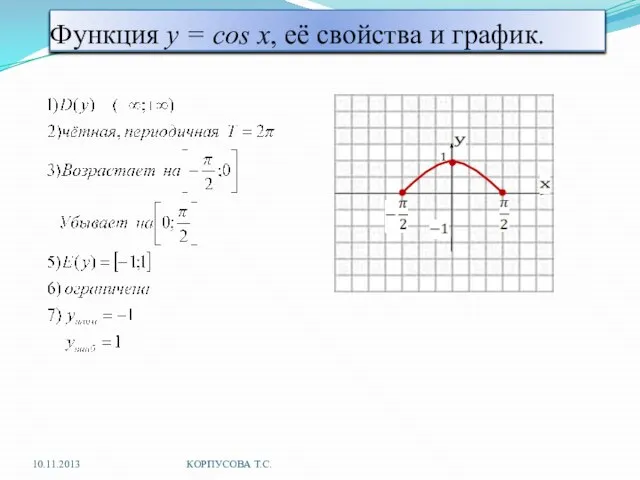
Функция y = cos x, её свойства и график.
10.11.2013
КОРПУСОВА Т.С.

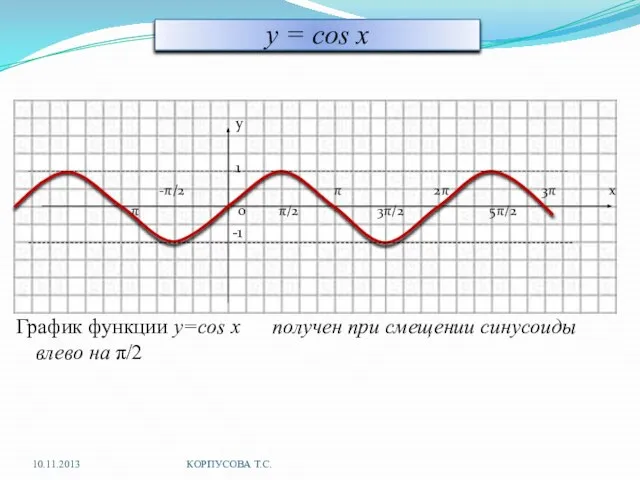
y = cos x
у
1
-π/2 π 2π 3π х
-π 0 π/2 3π/2 5π/2
-1
График функции у=cos x получен при смещении синусоиды влево на π/2
10.11.2013
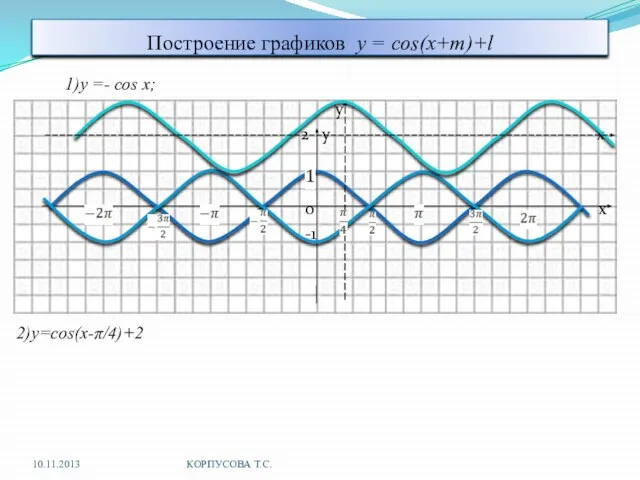
КОРПУСОВА Т.С.

Построение графиков y = cos(x+m)+l
1)y =- cos x;
y
2 y x
0 x
-1
2)y=cos(x-π/4)+2
10.11.2013
КОРПУСОВА Т.С.

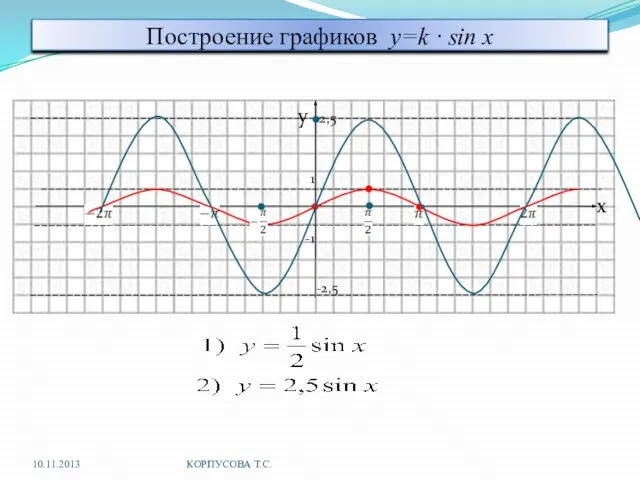
Построение графиков y=k · sin x
y 2,5
1
x
-1 -2,5
10.11.2013
КОРПУСОВА Т.С.

Нахождение периода тригонометрических функций
Если y=f(x) периодическая и имеет наименьший положительный период Т₁, то функция
y=A· f(kx+b), где А, k и b постоянные, а k ≠ 0 , также периодична с периодом
Примеры:
10.11.2013
КОРПУСОВА Т.С.
1) y=sin6x +2, Т₁=2π
T₁=2π

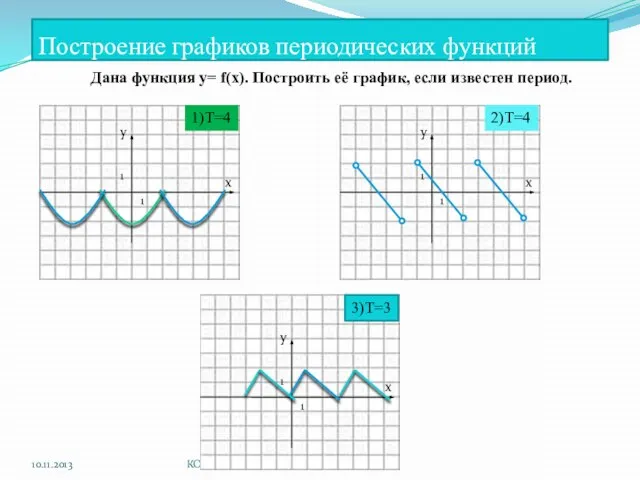
Построение графиков периодических функций
10.11.2013
КОРПУСОВА Т.С.
y
x
1
1
1)T=4
2)T=4
Дана функция у= f(x). Построить её график, если известен период.
3)T=3

.
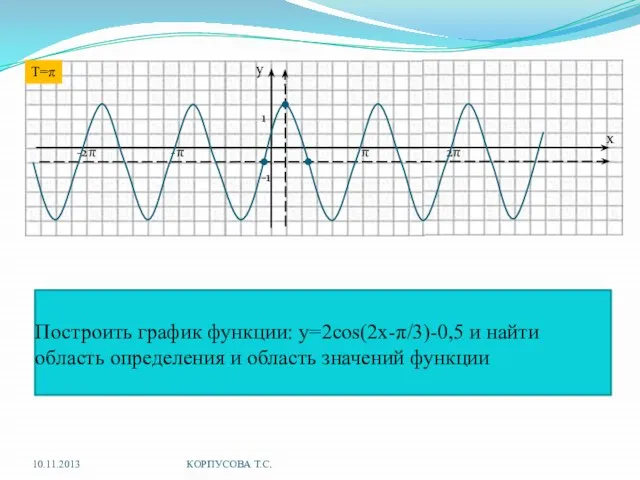
Построить график функции: y=2cos(2x-π/3)-0,5 и найти область определения и область значений функции
10.11.2013
КОРПУСОВА Т.С.
T=π