Презентация на тему История числа

Содержание
Как мы считаем
Счеты в разных странах
Способы счёта
Пальцевой счет
Возникновение чисел

Как мы считаем
Искусство счета развивалось с развитием человечества. В те времена, когда человек лишь собирал в лесу плоды и охотился, ему для счета хватало четырех слов: один, два, три и много. Именно так считают и сейчас некоторые племена, живущие в джунглях Южной Америки.

Однако, когда люди начали заниматься животноводством и земледелием, то им уже стало необходимо пересчитывать коз в стаде или количество корзин с выращенными плодами (которых было больше трех), заготовленными на зиму.

Если в какой-то бороздке при счете набиралось более 10 камешков, их снимали и добавляли один камешек в следующем разряде.
Римляне усовершенствовали абак, перейдя от деревянных досок, песка и камешков к мраморным доскам с выточенными желобками и мраморными шариками.

Обнаружена в раскопках так называемая "вестоницкая кость" с зарубками. Это позволяет историкам предположить, что уже 30тыс.лет.до н.э. наши предки были знакомы с зачатками счета.

Древнегреческий абак (доска или "саламинская доска" по имени острова Саламин в Эгейском море) представлял собой посыпанную морским песком дощечку. На песке проходились бороздки, на которых камешками обозначались числа. Одна бороздка соответствовала единицам, другая - десяткам и т.д.

Счеты в разных странах
Китайские счеты суан-пан состояли из деревянной рамки, разделенной на верхние и нижние секции. Палочки соотносятся с колонками, а бусинки с числами. У китайцев в основе счета лежала не десятка, а пятерка.

Она разделена на две части: в нижней части на каждом ряду располагаются по 5 косточек, в верхней части - по две. Таким образом, для того чтобы выставить на этих счетах число 6, ставили сначала косточку, соответствующую пятерке, и затем прибавляли одну в разряд единиц.

На Руси долгое время считали по косточкам, раскладываемым в кучки. Примерно с XV века получил распространение "дощаный счет". "Дощаный счет" почти не отличался от обычных счетов и представлял собой рамку с укрепленными горизонтальными веревочками, на которые были нанизаны просверленные сливовые или вишневые косточки.
«Русский щот»

Способы счёта
Способов счета было придумано немало: делались зарубки на палке по числу предметов, завязывались узлы на веревке, складывались в кучу камешки. Но палку с зарубками с собой не возьмёшь, да и камни таскать не очень приятно, а пастуху нужно знать – не отбилась ли какая коза от стада.

И тут на помощь приходят пальцы рук – отличный счетный материал, им до сих пор пользуются не только первоклассники. А если предметов больше десяти?

Так, для выражения числа «двадцать» индейцы из Южной Америки противопоставляют пальцы на руках пальцам на ногах.

Конечно, можно использовать и пальцы на ногах, а дальше? Тут уже ничего не оставалось делать, как придумать десятичную систему, которой мы пользуемся сейчас: считаем десятки; когда наберется десять десятков, называем их сотней; потом десять сотен – тысячей.

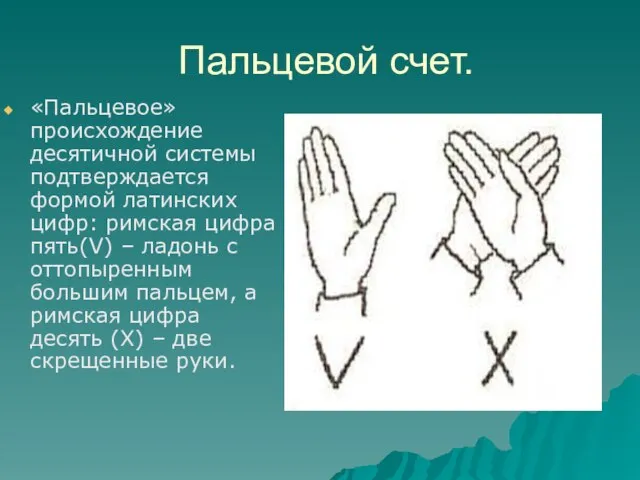
«Пальцевое» происхождение десятичной системы подтверждается формой латинских цифр: римская цифра пять(V) – ладонь с оттопыренным большим пальцем, а римская цифра десять (X) – две скрещенные руки.
Пальцевой счет.

Индейцы племени майя в Америке считали пятёрками: одна пятерка – единица следующего разряда, пять пятерок – новый разряд и т.д. Ясно, что они пользовались пальцами только одной руки.

Некоторые племена использовали только четыре пальца одной руки, однако при этом учитывали, что каждый палец состоит из трех фаланг, т.е имели в распоряжении двенадцать объектов счета

Так возникла дюжина, которая сто лет назад была широко распространена и в Европе, и в России, но постепенно уступила свое место десятке. До сих пор в Европе дюжинами считают пуговицы, носовые платки, куриные яйца, и многое другое, что продается поштучно.

Все знают, что тысяча тысяч – это миллион. Тысяча миллионов называется биллионом или миллиардом («би» - по-латыни – два). Тысяча миллиардов, т.е. 1 000 000 000 000 – триллион («три» - по-латыни – три), дальше 1 000 000 000 000 000 – квадриллион (квадра – четыре), дальше квинтиллион, секстиллион, октиллион, нониллион дециллион.

Большие числа возникают в астрономии, часто говорят об «астрономических числах», поскольку массы звезд и расстояния между ними выражаются действительно большими числами, однако физики подсчитали, что количество атомов – мельчайших частиц вещества – во всей Вселенной не превосходит числа, выражаемого единицей со ста нулями. Это число получило специальное название – гугол.

Возникновения чисел.
Мы привыкли пользоваться благами цивилизации – автомобилем, телефоном, телевизором и прочей техникой, делающей нашу жизнь легче и интереснее. Тысячи изобретений потребовалось для этого, но самым важным из них были первые – колесо и число. Без них не было бы всего нашего технического великолепия. Казалось бы, что понятие числа должно возникнуть одновременно с умением считать, но это далеко не так.

Замечено, что считать до пяти умеют и кошки и свиньи, но чтобы перейти от пяти предметов к числу «пять», требовалось великое открытие, и вот почему. Пять собак или пять свиней – это совсем не то, что пять орехов.

Пять собак или пять свиней – это совсем не то, что пять орехов.
Ведь пять орехов – очень мало, съел – и не заметил, а пять свиней – очень много, их хватит, чтобы долго кормиться большой семье. Пять собак – это стая, которая может хорошо защитить от диких зверей, а пять блох на собаке и разглядеть-то трудно. Разве можно их сравнивать?

Знаменитый русский путешественник Н.Н.Миклухо-Маклай, проведший много лет среди туземцев на островах Тихого океана, обнаружил, что у некоторых племен имеется три способа счета: для людей, для животных и для утвари, оружия и прочих неодушевленных предметов. То есть там в то время еще не появилось понятие числа, не было осознано, что три ореха, три козы и три ребенка обладают общим свойством – их количество равно трем.

Итак, появились числа 1,2,3,…, которыми можно выразить количество коров в стаде, деревьев в саду, волос на голове. Эти числа впоследствии получили название натуральных. Гораздо позднее появился ноль, которым обозначали отсутствие рассматриваемых предметов.

Математика Допетровской Руси.
Древнейшая русская математическая рукопись, сохранившаяся до наших дней, датируется 1136 годом – временем, когда единая Киевская Русь стала неудержимо разваливаться на мелкие, враждующие княжества. Автором этой рукописи был новгородский дьякон и «числолюбец» по имени Кирик.

Благодаря запискам Кирика, мы можем судить, что уровень математических знаний в XII веке был на Руси не ниже, чем в Западной Европе. Записки содержат значки на суммирование прогрессий, связанные с приплодом коров и овец, исчисление количества месяцев, недель и дней, прошедших со дня сотворения мира.

В Древней Руси десять тысяч называли «тьма». Отсюда выражение «тьма народу». 100 000 - легион, или неведий, 1 000 000 – леодр.
Миллион
Сто тысяч