Слайд 2
Цели:
ввести понятие квадратичной функции;
научится строить график функции у=ах2 + ах

+с и описывать свойства данной функции по графику;
установить закономерность между графиком функции у=ах2 и значением коэффициента а.
Слайд 3Два жучка бежали в домик.
Им навстречу муравей.
Сколько будет насекомых?
Сосчитай - ка их

скорей!
Слайд 4Определение.
Квадратичной функцией называется функция, которую можно задать формулой вида у=ах2+bx+c, где

х – независимая переменная, а, b и с – некоторые числа, причем а≠0.
Слайд 5Из приведенных примеров укажите те функции,
которые являются квадратичными. Для квадратичных
функций

назовите коэффициенты.
Слайд 9Диктант.
Функция у=ах2, ее график и свойства.

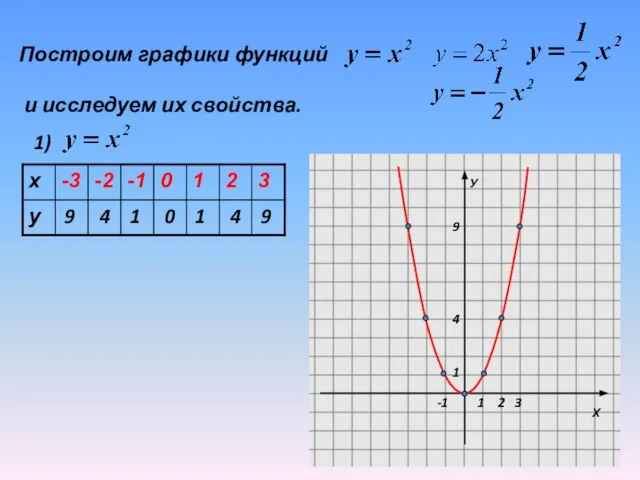
Слайд 10Построим графики функций
и исследуем их свойства.
1)
9
4
1
0
1
4
9
Слайд 11Построим графики функций
и исследуем их свойства.
1)
9
4
1
0
1
4
9
1. D(y): R
2. у=0, если
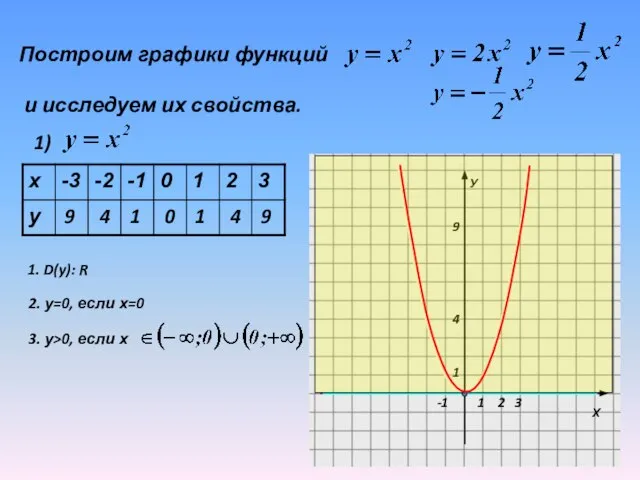
Слайд 12Построим графики функций
и исследуем их свойства.
1)
9
4
1
0
1
4
9
1. D(y): R
2. у=0, если
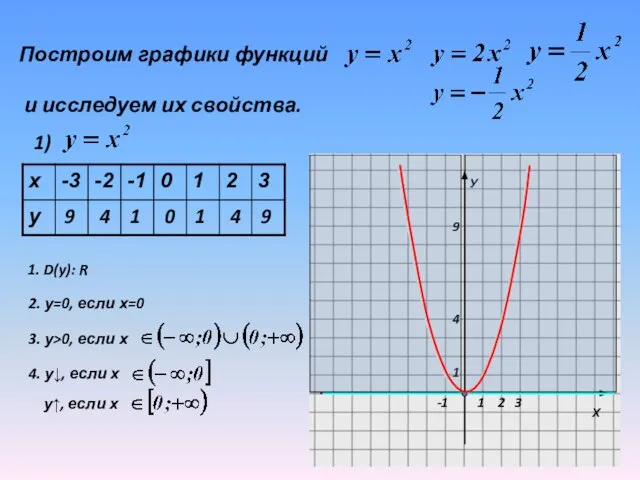
х=0
3. у>0, если х
4. у↓, если х
у↑, если х
Слайд 13Построим графики функций
и исследуем их свойства.
1)
9
4
1
0
1
4
9
1. D(y): R
2. у=0, если
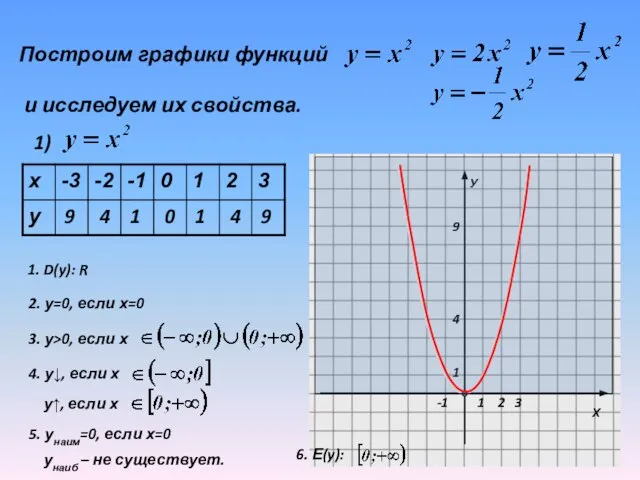
х=0
3. у>0, если х
4. у↓, если х
у↑, если х
5. унаим=0, если х=0
унаиб – не существует.
6. Е(y):
Слайд 14Построим графики функций
и исследуем их свойства.
2)
18
8
2
0
2
8
18
Есть ли различия в
свойствах
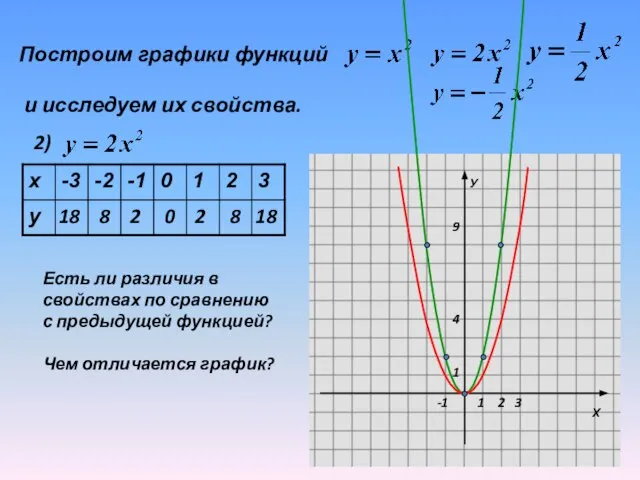
по сравнению
с предыдущей функцией?
Чем отличается график?
Слайд 15 График функции у=kx2 может быть получен из графика функции у=x2 путем

растяжения его вдоль оси Оу в k раз (k-натуральное число).
Слайд 16Построим графики функций
и исследуем их свойства.
3)
4,5
2
0,5
0
0,5
2
4,5
Есть ли различия в
свойствах
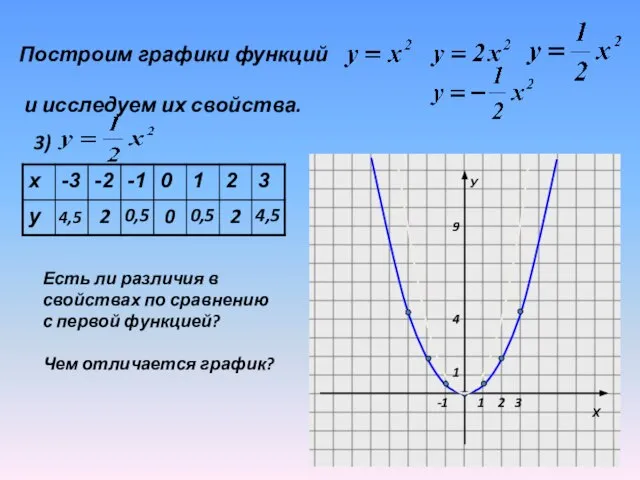
по сравнению
с первой функцией?
Чем отличается график?
Слайд 17График функции у= x2 может
быть получен из графика функции у=x2 путем

сжатия его вдоль оси Оу в k раз (k-натуральное число).
Слайд 18Построим графики функций
и исследуем их свойства.
4)
-4,5
-2
-0,5
0
-0,5
-2
-4,5
Есть ли различия в
свойствах
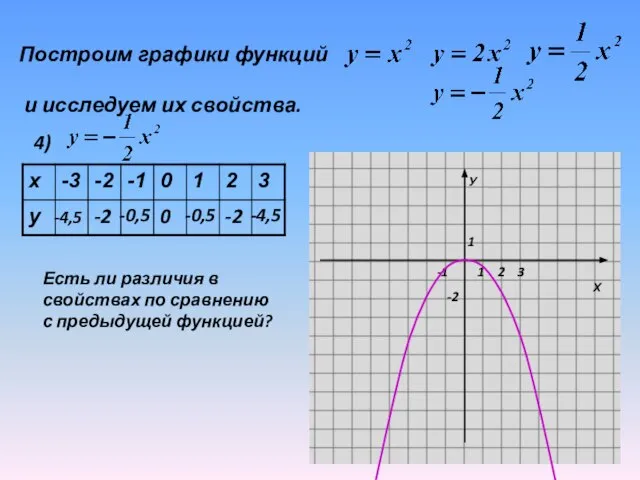
по сравнению
с предыдущей функцией?
Слайд 19Построим графики функций
и исследуем их свойства.
4)
-4,5
-2
-0,5
0
-0,5
-2
-4,5
1. D(y): R
2. у=0, если
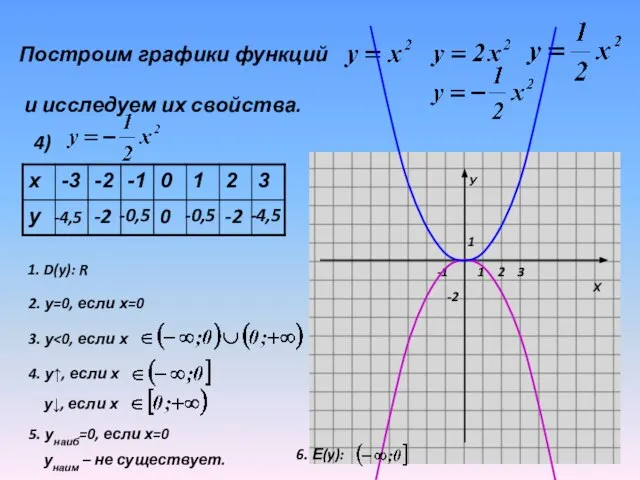
х=0
3. у<0, если х
4. у↑, если х
у↓, если х
5. унаиб=0, если х=0
унаим – не существует.
6. Е(y):
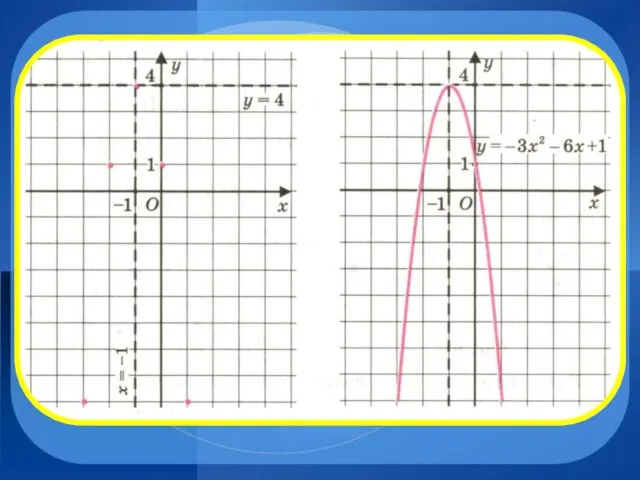
Слайд 20 График функции у=ах2 симметричен графику функции у=-ах2 относительно оси Ох.
Если а>0,

то ветви параболы направлены…
Если а<0, то ветви параболы
направлены…


















 Трудный разговор
Трудный разговор Особенности административно-территориального устройства России
Особенности административно-территориального устройства России Сборник правовых актов Совета Европы о сохранении культурного наследия (часть 2)Compendium of legal acts of Council of Europe on the protection of cultural heritage(par
Сборник правовых актов Совета Европы о сохранении культурного наследия (часть 2)Compendium of legal acts of Council of Europe on the protection of cultural heritage(par Презентация на тему Верховный тайный совет
Презентация на тему Верховный тайный совет Приключения Алисы в стране чудес
Приключения Алисы в стране чудес L'Europe, LA VRAIE, celle de toujours, va de Brest à Vladivostock
L'Europe, LA VRAIE, celle de toujours, va de Brest à Vladivostock Финансовые институты и банковская система
Финансовые институты и банковская система Развитиелогического мышленияна уроках математики
Развитиелогического мышленияна уроках математики The roaring twenties
The roaring twenties 1
1 Метаболизм. Энергетический обмен
Метаболизм. Энергетический обмен Всемирный день моря
Всемирный день моря Гуляев Степан Иванович
Гуляев Степан Иванович АМЕРИКАНСКИЙ АНГЛИЙСКИЙ: КРАТКИЙ ЭКСКУРС В ИСТОРИЮ И ПРАКТИКУ
АМЕРИКАНСКИЙ АНГЛИЙСКИЙ: КРАТКИЙ ЭКСКУРС В ИСТОРИЮ И ПРАКТИКУ Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Школа
Школа Обзор детских образовательных Интернет-ресурсов 2010
Обзор детских образовательных Интернет-ресурсов 2010 Формирование познавательной активности у детей младшего дошкольного возраста методом экспериментирования при ознакомлении с пр
Формирование познавательной активности у детей младшего дошкольного возраста методом экспериментирования при ознакомлении с пр Инфабрика. Первый частный музей современного сибирского искусства
Инфабрика. Первый частный музей современного сибирского искусства Энергоэффективный город Новочебоксарск
Энергоэффективный город Новочебоксарск АРХИМЕДОВА СИЛА
АРХИМЕДОВА СИЛА Собирательные числительные
Собирательные числительные  Полимерные материалы
Полимерные материалы Панно-оригами из ткани
Панно-оригами из ткани Аттестационная работа. Рабочая программа внеурочной деятельности развития познавательных способностей учащихся 5 - х классов
Аттестационная работа. Рабочая программа внеурочной деятельности развития познавательных способностей учащихся 5 - х классов Тает лёд с Алексеем Ягудиным
Тает лёд с Алексеем Ягудиным Введение в космологию
Введение в космологию Общественный и государственный строй централизованного русского государства
Общественный и государственный строй централизованного русского государства