Содержание
- 2. Цель: повторяя материал курса математики 5–6 классов, ввести термины: математический язык, математическая модель, не давая им
- 3. Числовые и алгебраические выражения Что такое математический язык Что такое математическая модель Линейное уравнение с одной
- 4. и т.д. У каждой дисциплины свои объекты изучения, свои методы познания реальной действительности Числовые и алгебраические
- 5. Числовым выражением называют всякую запись, составленную из чисел и знаков арифметических действий Пример 1: Обозначим числитель
- 6. В процессе решения примера вспомнили и применили следующие сведения: Порядок арифметических действий. Переместительный закон сложения: а+в=в+а.
- 7. Число, которое получается в результате упрощений числового выражения, называют значением числового выражения. Если дано алгебраическое выражение,
- 8. На нуль делить нельзя! В тех случаях, когда возникает такая ситуация делаем вывод, что выражение не
- 9. Что такое математический язык Цель: сформировать понимание учащимися того, что математика – предмет, позволяющий правильно ориентироваться
- 10. На математическом языке многие утверждения выглядят яснее и прозрачнее, чем на обычном. Во всяком языке есть
- 11. Вывод главное назначение математического языка – способствовать организации деятельности.
- 12. Что такое математическая модель Цель: сформировать понимание учащимися сути термина «математическое моделирование». Привести примеры, показывающие, как
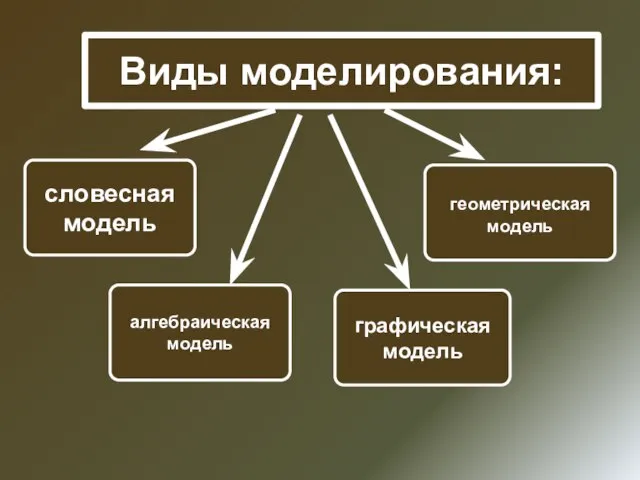
- 13. Виды моделирования: словесная модель геометрическая модель алгебраическая модель графическая модель
- 14. Алгебра занимается тем, что описывает различные реальные ситуации на математическом языке в виде математических моделей, а
- 15. Линейное уравнение с одной переменной Цель: повторить известные из курса 5–6 класса линейные уравнения с одной
- 16. Одним из самых простых и в то же время очень важных видов математических моделей реальных ситуаций
- 17. Что значит решить линейное уравнение ? Решить линейное уравнение – это значит найти все те значения
- 18. Линейным уравнением с одной переменной x называют уравнение вида ax+b=0, где a и b – любые
- 19. Алгоритм решения линейного уравнения ax+b=0 в случае, когда a≠0 Преобразовать уравнение к виду a x =
- 20. Алгоритм решения линейного уравнения Если уравнение содержит скобки, то их надо открыть по правилу раскрытия скобок
- 21. Методы и приемы применяемые при решении уравнений Приведение подобных слагаемых Правила раскрытия скобок Прием переноса слагаемых
- 22. Цель: повторить понятие координатной прямой (координатной оси), правило нахождения точки по заданной координате и правило отыскания
- 23. Нужно уметь свободно переходить от одного вида математической модели к другому, выбирать то, что удобнее. В
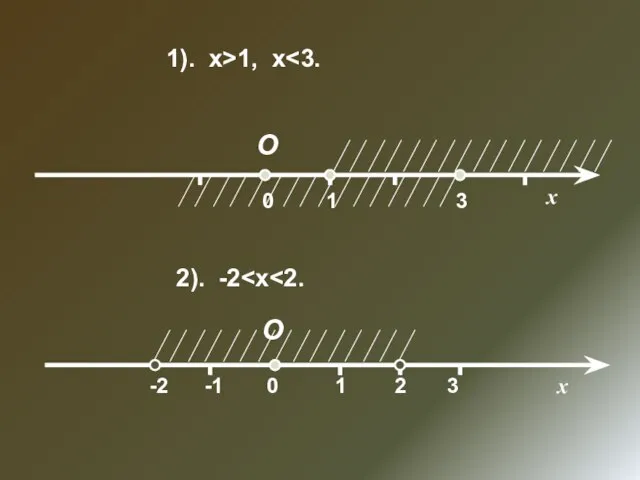
- 24. О 0 х 1 3 1). х>1, х 2). -2 О 0 х -2 -1 1
- 25. Сводная таблица числовых промежутков
- 26. Привести примеры: числовых выражений; алгебраических выражений; порядка выполнения действий в числовых выражениях; переместительного и сочетательного законов
- 27. №1. Укажите числовые и буквенные выражения А) 4,16+2,5+6,04+3,5; Б) х+5; В) 8с - 12d; Г) ;
- 29. Скачать презентацию























 Проектирование региональных МИС
Проектирование региональных МИС О повышении энергоэффективности в Республике Беларусь
О повышении энергоэффективности в Республике Беларусь Презентация на тему Виктор Павлович Кочубей
Презентация на тему Виктор Павлович Кочубей Planning. FL lesson
Planning. FL lesson Мезень
Мезень День энергетика
День энергетика Допинг
Допинг Презентация на тему Выталкивающая сила (7 класс)
Презентация на тему Выталкивающая сила (7 класс) Программа ЮНИДО по содействию выполнению Стокгольмской Конвенции по Стойким Органическим Загрязнителям Ищенко В.Я.
Программа ЮНИДО по содействию выполнению Стокгольмской Конвенции по Стойким Органическим Загрязнителям Ищенко В.Я. Симметрия
Симметрия О методах тренировки мышц кистей и предплечий в гиревом спорте
О методах тренировки мышц кистей и предплечий в гиревом спорте Молодежь в современном обществе
Молодежь в современном обществе НЕДЕЛЯ РУССКОГО ЯЗЫКА И ЛИТЕРАТУРЫ
НЕДЕЛЯ РУССКОГО ЯЗЫКА И ЛИТЕРАТУРЫ Лесные зоны России
Лесные зоны России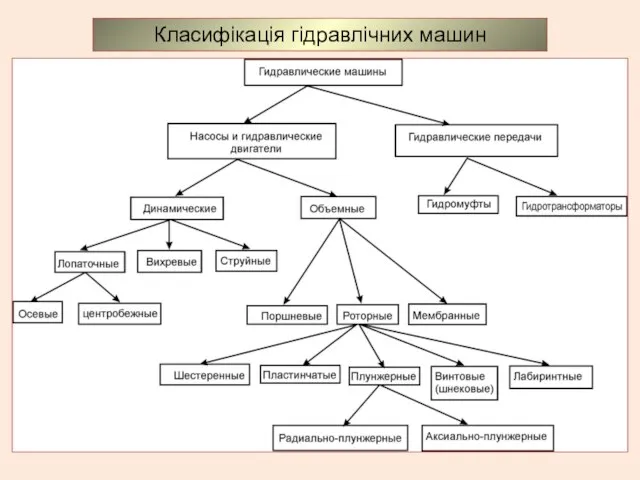 Класифікація гідравлічних машин
Класифікація гідравлічних машин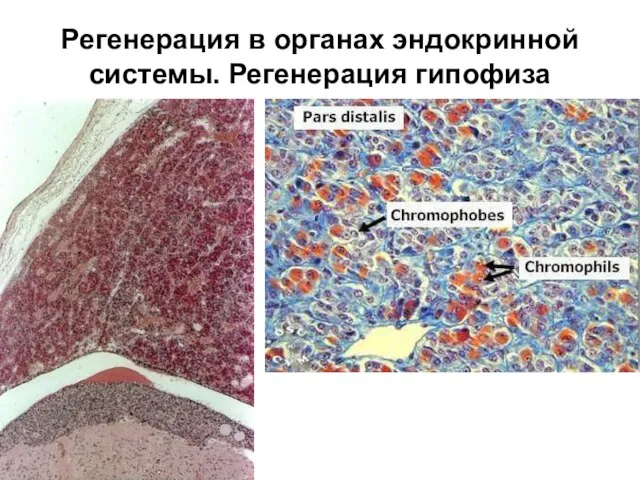 Регенерация в сердечно-сосудистой и эндокринной системе
Регенерация в сердечно-сосудистой и эндокринной системе Южная Европа. Италия
Южная Европа. Италия Влияние цвета на настроение человека
Влияние цвета на настроение человека Independent work
Independent work Презентация на тему Вишня
Презентация на тему Вишня  Декоративные панели
Декоративные панели Разработка авторских материалов для поддержки дистанционного обучения Учитель химии ГОУ СОШ № 279 Зайцева Н.С.
Разработка авторских материалов для поддержки дистанционного обучения Учитель химии ГОУ СОШ № 279 Зайцева Н.С. Неаполь скифский
Неаполь скифский Кинетика химических реакций.Химическое равновесие
Кинетика химических реакций.Химическое равновесие Применение распределительного свойства умножения 6 класс
Применение распределительного свойства умножения 6 класс Основы социальной информатики
Основы социальной информатики Трудные вопросы при подготовке к ЕГЭ по русскому языку
Трудные вопросы при подготовке к ЕГЭ по русскому языку Презентация на тему о введении в школе ГТО
Презентация на тему о введении в школе ГТО