Презентация на тему Модели в механике. Система отчета.Траектория. Длина пути

Механика делится на три раздела..
Кинематика изучает движение тел, не рассматривая
причины, которые это движение обуславливают.
Классическая механика рассматривает пространство и
время как объективные формы существования материи,
но в отрыве друг от друга и от движения материальных тел.
Такой подход соответствовал уровню знаний времени
Галилей и Ньютона.
Статика изучает законы равновесия системы тел.
Если известны законы движения тел, то из них можно
установить и законы равновесия. Поэтому законы статики отдельно от законов динамики физика не рассматривает.
Динамика изучает законы движения тел и причины,
которые вызывают или изменяют это движение.

Механика для описания движения тел в зависимости от условий конкретных задач использует разные
физические модели.
Понятие материальной точки – абстрактное (первая абстракция), но его введение облегчает решение практических задач.
Простейшей моделью является материальная точка – тело, обладающее массой, размерами которого в данной задаче можно пренебречь.

Произвольное макроскопическое тело или систему тел можно мысленно разбить на малые взаимодействующие между собой части, каждая из которых рассматривается как материальная точка. Тогда изучение движения произвольной системы тел сводится к изучению системы материальных точек.
В механике сначала изучают движение одной материальной точки, а затем переходят к изучению движения системы материальных точек.

Абсолютным твердым телом называется тело,
которое ни при каких условиях не может дефор-
мироваться и при всех условиях расстояние
между двумя точками (или точнее между двумя
частицами) этого тела остается постоянным.
Под воздействием тел друг на друга тела могут
деформироваться, т.е. изменять свою форму и размеры.
Поэтому в механике вводится еще одна модель – абсолютно твердое тело (вторая абстракция).

Вращательное движение – это движение, при
котором все точки тела движутся по окружностям,
центры которых лежат на одной и той же прямой,
называемой, осью вращения.
Любое движение твердого тела можно представить как комбинацию поступательного и вращательного движений.
Поступательное движение – это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению.

Движение тел происходит в пространстве и во времени. Поэтому для описания движения материаль-ной точки надо знать, в каких местах пространства эта точка находилась и в какие моменты времени она проходила то или иное положение.
Положение материальной точки определяется по
отношению к какому-либо другому, произвольно выбранному телу, называемому телом отсчета.
Система отсчета – совокупность системы координат и часов, связанных с телом отсчета.

В декартовой системе координат положение точки А в
данный момент времени по отношению к этой системе
характеризуется тремя координатами или
радиус-вектором
В общем случае ее движение определяется скалярными
уравнениями
которые эквивалентны векторному
уравнению
(1.1)
(1.2)
При движении материальной точки ее координаты с
течением времени изменяются.
Уравнения (1.1) и (1.2) называются
кинематическими уравнениями
материальной точки.

Число независимых координат, полностью определяю-
щих положение точки в пространстве, называется
числом степеней свободы. Если материальная точка
свободно движется в пространстве, то она обладает
тремя степенями свободы (координаты ); если
она движется по некоторой плоскости, то двумя степе-
нями свободы; если вдоль некоторой линии, то одной
степенью свободы.
Исключая время в уравнениях (1.1) и (1.2), получим уравнение траектории движения материальной точки.
Траектория движения материальной точки – линия,
описываемая этой точкой в пространстве.
В зависимости от формы траектории движение может быть прямолинейным или криволинейным.

Рассмотрим движение материальной точки вдоль
произвольной траектории. Отсчет времени начнем с
момента, когда точка находилась в положении А.
Длина участка траектории АВ, пройденного
материальной точкой с момента начала отсчета
времени, называется длиной пути
Длина пути есть скалярная функция времени

Вектор , проведенный из начального
положения движущейся точки в положение ее в данный
момент времени (приращение радиус-вектора точки за
рассматриваемый промежуток времени), называется
перемещением.
При прямолинейном движении
вектор перемещения совпадает
с соответствующим участком
траектории и модуль
перемещения равен
пройденному пути
В общем случае

С К О Р О С Т Ь
Для характеристики движения материальной точки
вводится векторная величина – скорость, которая
определяет как быстроту движения, так и направление
движения в данный момент времени.
Пусть материальная точка движется по произвольной
криволинейной траектории таким
образом, что в момент времени
ей соответствует радиус-вектор .
В течение малого промежутка
времени точка пройдет
путь и получит элементарное
(бесконечно малое)
перемещение

Вектором средней скорости называется отношение
приращения радиус-вектора точки к промежутку
времени
Направление вектора средней скорости совпадает с направлением
При неограниченном уменьшении
средняя скорость стремится к
предельному значению, которое
называется мгновенной
скоростью

Мгновенная скорость есть векторная величина,
равная первой производной радиус-вектора движущей-
ся точки по времени. Поскольку секущая в пределе
совпадает с касательной, то вектор мгновенной
скорости направлен по касательной к траектории
в сторону движения.
Средняя скорость неравномерного
движения

Модуль мгновенной скорости равен первой
производной пути по времени
При неравномерном движении модуль мгновенной
скорости с течением времени изменяется.
Так как (равенство только в случае
прямолинейного движения), то

Если выражение проинтегрировать по
времени в пределах от до ,
то найдем длину пути,
пройденного точкой
за время
В случае равномерного движения числовое значение
мгновенной скорости постоянно; тогда последнее
выражение примет вид
В общем случае, длина пути, пройденного точкой за
промежуток времени от до ,
дается интегралом

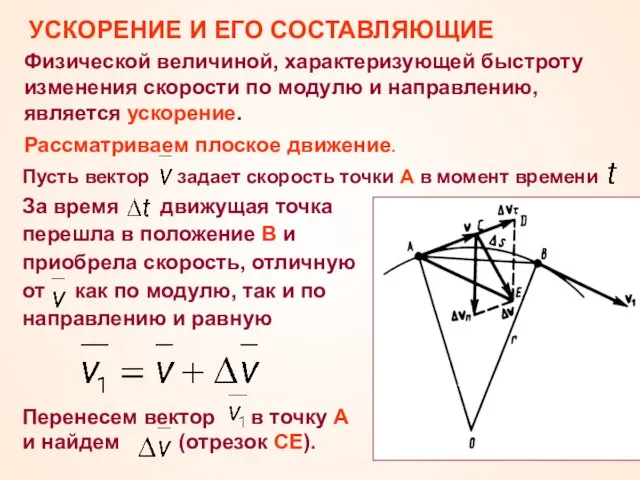
За время движущая точка
перешла в положение В и
приобрела скорость, отличную
от как по модулю, так и по
направлению и равную
УСКОРЕНИЕ И ЕГО СОСТАВЛЯЮЩИЕ
Физической величиной, характеризующей быстроту
изменения скорости по модулю и направлению,
является ускорение.
Рассматриваем плоское движение.
Пусть вектор задает скорость точки А в момент времени
Перенесем вектор в точку А
и найдем (отрезок СЕ).

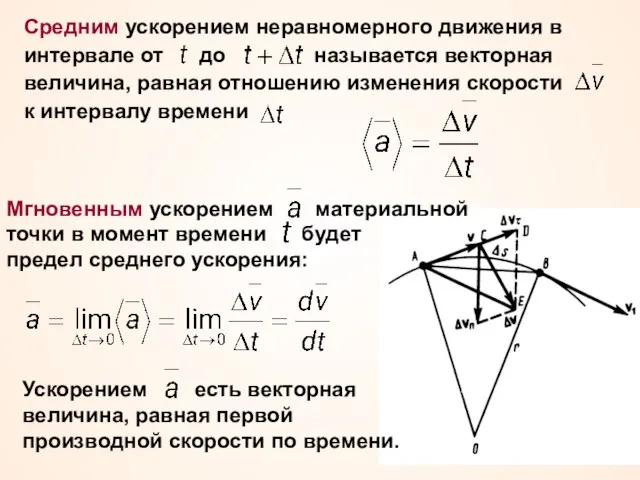
Средним ускорением неравномерного движения в
интервале от до называется векторная
величина, равная отношению изменения скорости
к интервалу времени
Мгновенным ускорением материальной
точки в момент времени будет
предел среднего ускорения:
Ускорением есть векторная
величина, равная первой
производной скорости по времени.

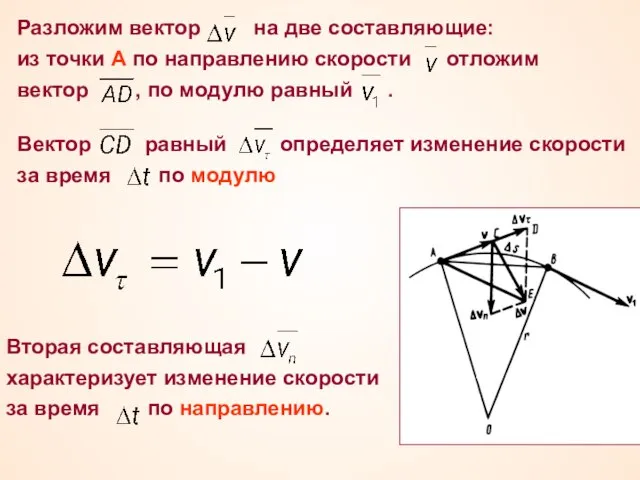
Разложим вектор на две составляющие:
из точки А по направлению скорости отложим
вектор , по модулю равный .
Вектор равный определяет изменение скорости
за время по модулю
Вторая составляющая
характеризует изменение скорости
за время по направлению.

Тангенциальная составляющая ускорения
равна первой производной по времени от модуля
скорости, определяя тем самым быстроту изменения
скорости по модулю.
Вторая составляющая ускорения, равная
называется нормальной составляющей ускорения и
направлена по нормали к траектории к центру ее
кривизны (поэтому ее называют также центростреми-
тельным ускорением).

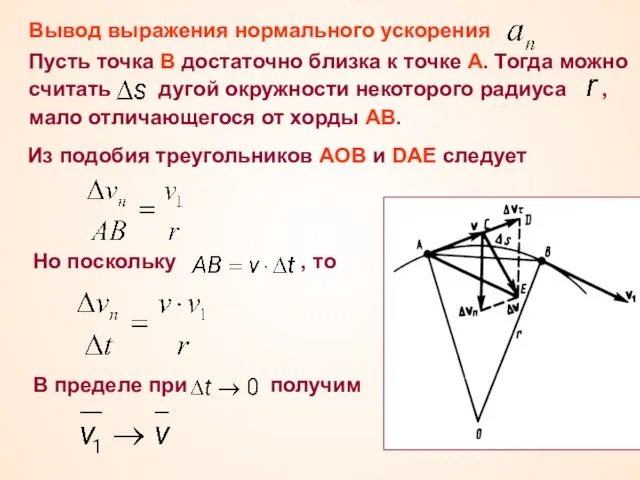
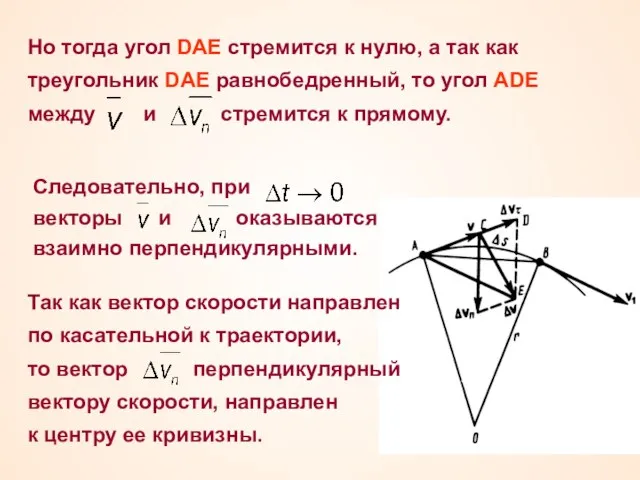
Вывод выражения нормального ускорения
Пусть точка В достаточно близка к точке А. Тогда можно
считать дугой окружности некоторого радиуса ,
мало отличающегося от хорды АВ.
Из подобия треугольников AOB и DAE следует
Но поскольку , то
В пределе при получим

Следовательно, при
векторы и оказываются
взаимно перпендикулярными.
Но тогда угол DAE стремится к нулю, а так как
треугольник DAE равнобедренный, то угол ADE
между и стремится к прямому.
Так как вектор скорости направлен
по касательной к траектории,
то вектор перпендикулярный
вектору скорости, направлен
к центру ее кривизны.

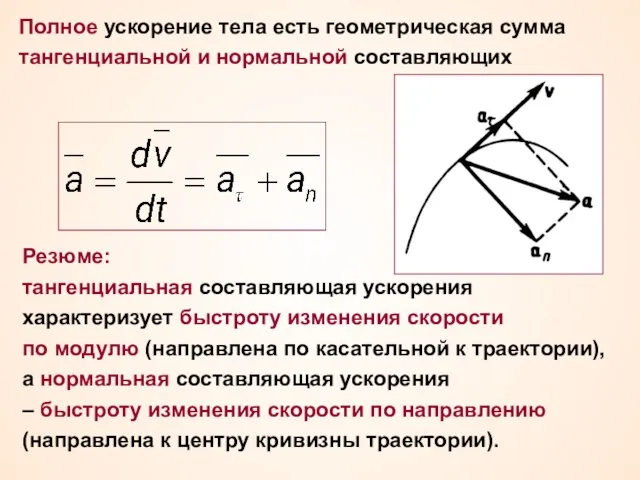
Полное ускорение тела есть геометрическая сумма
тангенциальной и нормальной составляющих
Резюме:
тангенциальная составляющая ускорения
характеризует быстроту изменения скорости
по модулю (направлена по касательной к траектории),
а нормальная составляющая ускорения
– быстроту изменения скорости по направлению
(направлена к центру кривизны траектории).

В зависимости от тангенциальной и нормальной
составляющих ускорения движение можно
классифицировать следующим образом:
1)
прямолинейное равномерное
движение;

2)
прямолинейное
равнопеременное движение;
Напомним, что
Если начальный момент времени , а начальная
скорость , то после интегрирования получим
Проинтегрировав эту формулу повторно в пределах от нуля
до произвольного момента времени , найдем, что длина
пути, пройденного точкой, в случае равнопеременного
движения

4)
При скорость по модулю не изменяется, а
изменяется по направлению. Из формулы
следует, что радиус кривизны должен быть постоянным.
Следовательно, движение по окружности является
равномерным;
прямолинейное движение с
переменным ускорением;
3)

5)
равномерное криволинейное движение;
7)
6)
криволинейное равнопеременное движение;
криволинейное движение с переменным ускорением.

УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ
Твердое тело вращается вокруг неподвижной оси.
Отдельные точки тела будут описывать окружности
разных радиусов, центры которых лежат на оси вращения.
Пусть некоторая точка движется по окружности радиуса .
Ее положение через промежуток времени зададим
углом .
Элементарные (бесконечно малые)
повороты можно рассматривать как
векторы (они обозначаются
или ).

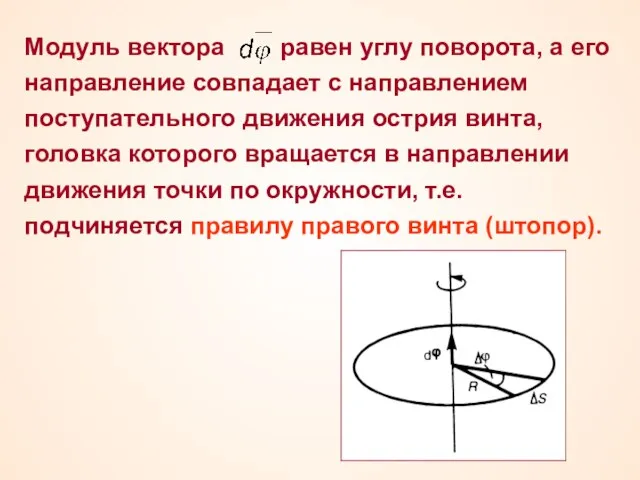
Модуль вектора равен углу поворота, а его направление совпадает с направлением
поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, т.е. подчиняется правилу правого винта (штопор).

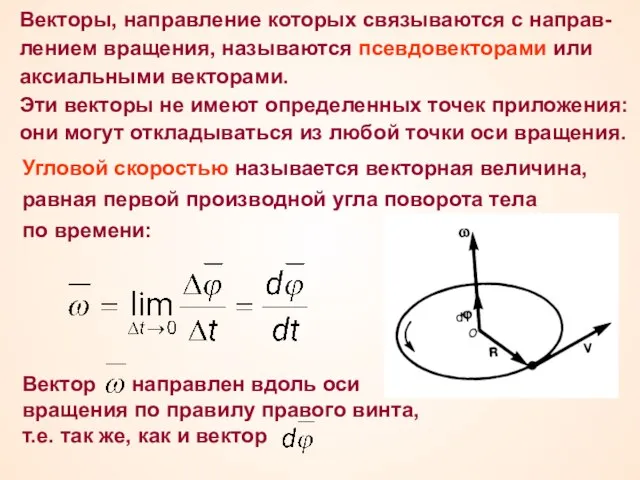
Векторы, направление которых связываются с направ-
лением вращения, называются псевдовекторами или
аксиальными векторами.
Эти векторы не имеют определенных точек приложения:
они могут откладываться из любой точки оси вращения.
Угловой скоростью называется векторная величина,
равная первой производной угла поворота тела
по времени:
Вектор направлен вдоль оси
вращения по правилу правого винта,
т.е. так же, как и вектор

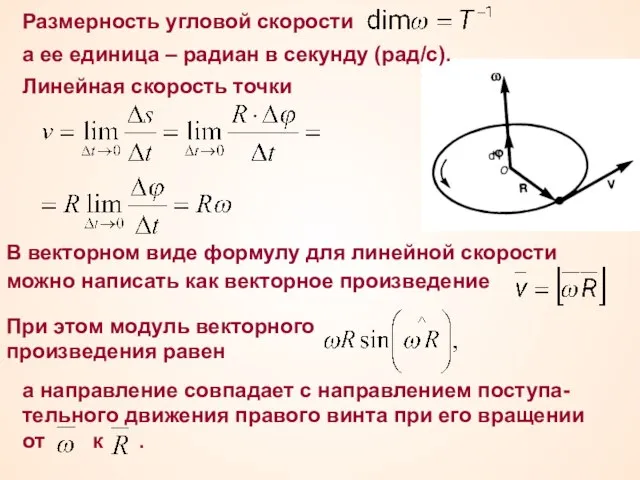
Размерность угловой скорости
а ее единица – радиан в секунду (рад/с).
Линейная скорость точки
В векторном виде формулу для линейной скорости
можно написать как векторное произведение
При этом модуль векторного
произведения равен
а направление совпадает с направлением поступа-
тельного движения правого винта при его вращении от к .

Если , то вращение равномерное и его
можно характеризовать периодом вращения .
Это время, за которое точка совершает один полный
оборот, т.е. поворачивается на угол
Так как промежутку времени соответствует
, то откуда
Число полных оборотов, совершаемых телом при
равномерном его движении по окружности, в единицу
времени называется частотой вращения:
откуда

Угловым ускорением называется векторная величина,
равная первой производной угловой скорости
по времени:
При вращении тела вокруг неподвижной оси вектор
углового ускорения направлен вдоль оси вращения в
сторону вектора элементарного приращения угловой
скорости.

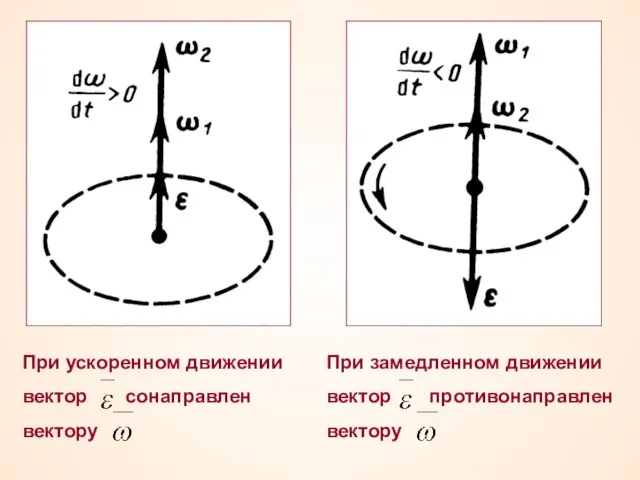
При ускоренном движении
вектор сонаправлен
вектору
При замедленном движении
вектор противонаправлен
вектору

Тангенциальная составляющая ускорения
и
Нормальная составляющая ускорения