Презентация на тему Молекулярно-кинетическая теория. Термодинамика

7.5. Закон Максвелла о распределении молекул идеального газа по скоростям
Закон Максвелла описывает функцию f(v), которая называется функцией распределения молекул по скоростям.
Функция распределения молекул идеального газа по скоростям:

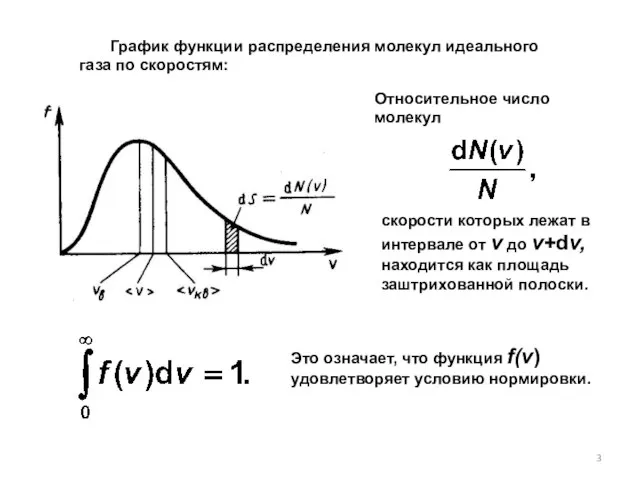
График функции распределения молекул идеального газа по скоростям:
скорости которых лежат в интервале от v до v+dv, находится как площадь заштрихованной полоски.
Это означает, что функция f(v) удовлетворяет условию нормировки.
Относительное число молекул

Наиболее вероятная скорость молекулы.
При повышении температуры максимум функции распределения молекул по скоростям сместится вправо.
Вероятной скоростью называется скорость, при которой функция распределения молекул идеального газа по скоро­стям максимальна.

Средняя скорость молекулы
:
Cредняя квадратичная скорость молекулы:

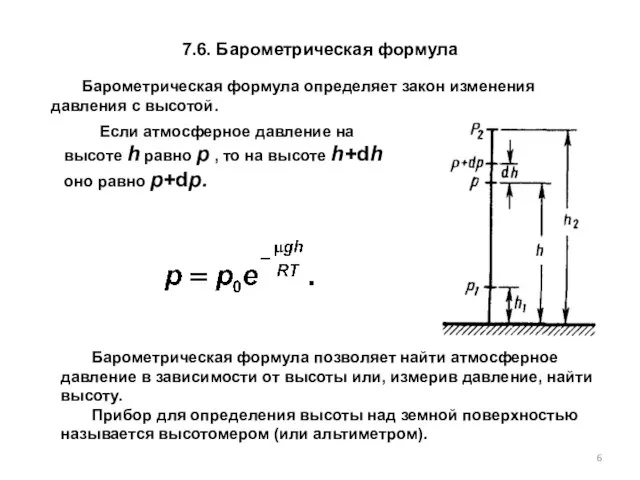
7.6. Барометрическая формула
Барометрическая формула позволяет найти атмос­ферное давление в зависимости от высоты или, измерив давление, найти высоту.
Прибор для определения высоты над земной поверхностью называется высотоме­ром (или альтиметром).
Барометрическая формула определяет закон изменения давления с высотой.
Если атмосферное давление на высоте h равно р , то на высоте h+dh оно равно p+dp.

7.7. Распределение Больцмана
где n – концентрация молекул на высоте h,
n0 – то же, на высоте h=0.
Обозначим: П=m0gh — потенциальная энергия молекулы, то:
Поскольку p=n k T, то барометрическую формулу можно записать в виде:
Заменим:
– формула распределения Больцмана.

7.8. Средняя длина свободного пробега молекул
Между столкновениями молекулы прохо­дят некоторый путь l, который называется длиной свободного пробега.
Под длиной пробега понимают среднюю длину свободного пробега молекул
.
Если
— среднее число столкновений, испытываемых одной молеку­лой газа за 1 с, то средняя длина свободного пробега:
Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d:

Среднее число столкновений за 1 с равно:
п — концентрация молекул, V = π d2
, откуда:
Расчеты показывают, что при учете движения других молекул:
Средняя длина свободного пробега молекул:

7.9. Эксперименты, подтверждающие молекулярно-кинетическую теорию
1. Броуновское движение.
Шотландский ботаник Роберт Броун (1773—1858). Интенсивность этого движения, называемого броуновским, повышается с ростом температуры среды, с уменьшением вязкости и размеров частиц.
Броуновское движение взвешенных частиц вызывается ударами молекул среды, в которой частицы взвешены.
Броуновское движение — беспорядочное движение микроскопических видимых, взвешенных в жидкости или газе частиц твердого вещества, вызываемое тепловым движением частиц жидкости или газа.

2. Опыт Штерна.
О. Штерн – немецкий физик (1888—1970).
Вдоль оси внутреннего цилиндра с щелью натянута платиновая проволока, покрытая слоем серебра, которая нагревается током при откачанном воздухе.
При нагревании серебро испаряется. Атомы серебра, вылетая через щель, попадают на внутреннюю поверхность второго цилиндра, давая изображение щели О.
Исследуя толщину осажденного слоя, можно оценить распределение молекул по скоростям, которое соответствует максвелловскому распределению.

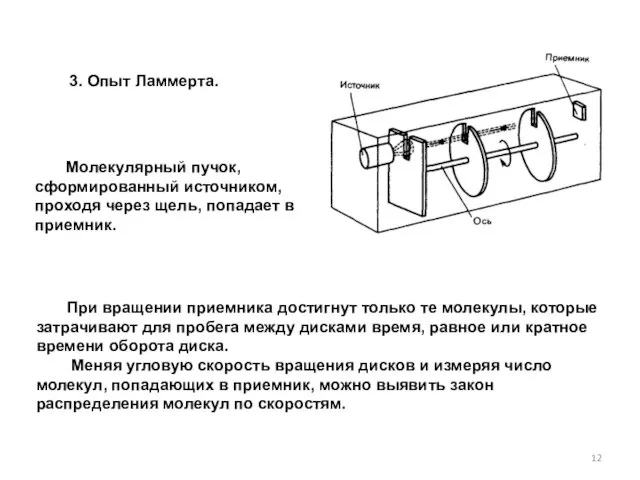
3. Опыт Ламмерта.
Молекулярный пучок, сформированный источником, проходя через щель, попадает в приемник.
При вращении приемника достигнут только те молекулы, которые затрачивают для пробега между дисками время, равное или кратное времени оборота диска.
Меняя угловую скорость вращения дисков и измеряя число молекул, попадающих в приемник, можно выявить закон распределения молекул по скоростям.

7.10. Явления переноса в термодинамических неравновесных системах
Явлениями переноса называют такие необратимые процессы в термодинамически неравновесных системах, в результате которых происходит пространственный перенос энергии, массы или импульса.
К явлениям переноса относятся:
теплопроводность (обусловлена переносом энергии),
диффузия (обусловлена переносом массы),
внутреннее трение (обусловлено переносом импульса).
Для простоты ограничимся рассмотрением одномерных явлений переноса.

1. Теплопроводность.
Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени происходит процесс выравнивания средних кинетических энергий молекул, т. е., иными словами, выравнивание температур.
Перенос энергии в форме теплоты подчиняется закону Фурье:
jE — плотность теплового потока, величина, определяемая энергией, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярную оси х,
λ — теплопроводность,
— градиент температуры, равный скорости изменения температуры на единицу длины х в направлении нормали к этой площадке.

— удельная теплоемкость газа при постоянном объеме (количество теплоты, необходимое для нагревания 1 кг газа на 1 К при постоянном объеме),
— плотность газа,
— средняя скорость теплового движения молекул,
— средняя длина свободного пробега.

2. Диффузия.
Диффузия – самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей или твердых тел.
Явление диффузии для химически однородного газа подчиняется закону Фука:
jm — плотность потока массы — величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси х,
D — диффузия (коэффициент диффузии),
dρ/dx — градиент плотности, равный скорости изменения плотности на единицу длины х в направлении нормали к этой площадке.

Диффузия D численно равна плотности потока массы при градиенте плотности, равном единице.
Согласно кинетической теории газов:

3. Внутреннее трение (вязкость).
Из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее — увеличивается.
Взаимодействие двух слоев согласно второму закону Ньютона можно рассматривать как процесс, при котором от одного слоя к другому в единицу времени передается импульс, по модулю равный действующей силе.
jp — плотность потока импульса — величина, определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси х через единичную площадку, перпендикулярную оси х,

— градиент скорости. Знак минус указывает, что импульс переносится в направлении убывания скорости
Динамическая вязкость η численно равна плотности потока импульса при градиенте скорости, равном единице; она вычисляется по формуле:
Из записанных выше формул вытекают простые зависимости между λ, D и η :

8. Основы термодинамики
При переходе системы из одного состояния в другое изменение внутренней энергии определяется только разностью значений внутренней энергии этих состояний и не зависит от пути перехода.
8.1. Внутренняя энергия и число степеней свободы
Термодина́мика — раздел физики, изучающий соотношения и превращения теплоты и других форм энергии.
Любая термодинамическая система обладает определенной внутренней энергией.
Внутренняя энергия — энергия хаотического (теплового) движения микрочастиц системы (моле­кул, атомов, электронов, ядер и т. д.) и энергия взаимодействия этих частиц.

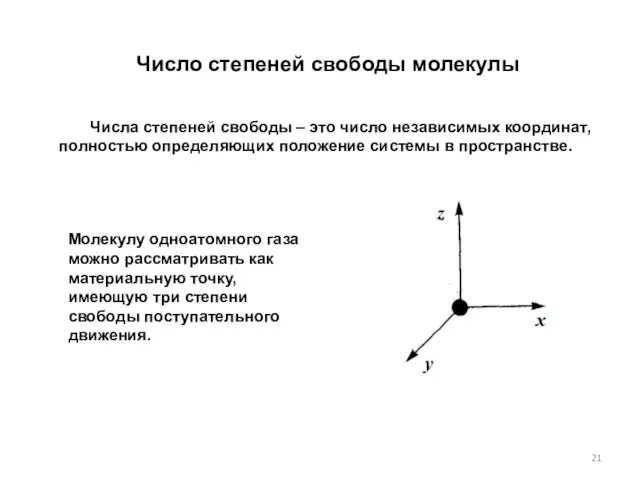
Число степеней свободы молекулы
Числа степеней свободы – это число независимых координат, полностью определяющих положение системы в пространст­ве.
Молекулу одноатомного газа можно рассматривать как матери­альную точку, имеющую три степени свободы поступательного движения.

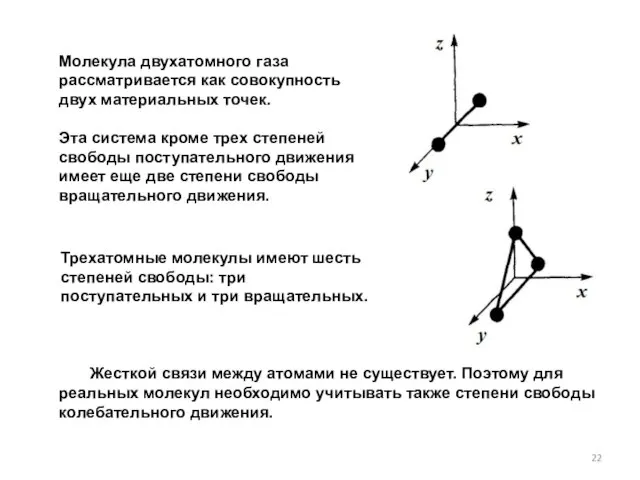
Молекула двухатомного газа рассматривается как совокупность двух материальных точек.
Эта система кроме трех степеней свободы поступательного движения имеет еще две степени свободы вращательного движения.
Трехатомные молекулы имеют шесть степеней свободы: три поступательных и три вращательных.
Жесткой связи между атомами не существует. Поэтому для реальных молекул необходимо учитывать также степени свободы колебательного движения.

Независимо от общего числа степеней свободы молекул три степени свободы всегда поступательные.
На каждую из них приходится в среднем одинаковая энергия, равная 1/3 значения <ε0> :

8.2. Закон Больцмана о равномерном распределении энергии по степеням свободы молекул
Cредняя энергия молекулы равна:
i — сумма числа поступательных, числа вращательных в удвоенного числа колебательных степеней свободы молекулы:
На каждую поступательную и вращательную степени свободы приходится кинетическая энергия:
На каждую колебательную степень свободы энергия:

Внутренняя энергия, отнесенная к одному молю газа, будет равна сумме кинетических энергий NA молекул:
Внутренняя энергия для произвольной массы т газа:
М — молярная масса, ν — количество вещества.

8.3. Первое начало термодинамики
Первое начало термодинамики характеризует закон сохранения энергии при изменении состояния системы.
Существует две формы изменения внутренней энергии системы: передача теплоты и работа против внешних.
Q - количество теплоты, полученным системой,
А - работа, совершаемая системой против внешних сил.
Первое начало термодинамики: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение работы против внешних сил.

Первое начало термодинамики в дифференциальной форме:
dU — бесконечно малое изменение внутренней энергии системы,
δA — элементар­ная работа,
δQ — бесконечно малое количество теплоты.
В этом выражении dU является полным дифференциалом, а δA и δQ таковыми не являются.
Т. е., если система вернулась в исходное состояние, то изменение внутренней энергии равно нулю, а работа при этом нулю не равна:

т. е. «вечный двигатель первого рода — периодически действующий двигатель, который совершал бы большую работу, чем сообщенная ему извне энергия, — невозможен».
Другая формулировка первого начала термодинамики
тогда, согласно первому началу термодинамики:
Если система периодически возвращается в первоначальное состояние, то измене­ние ее внутренней энергии равно нулю:

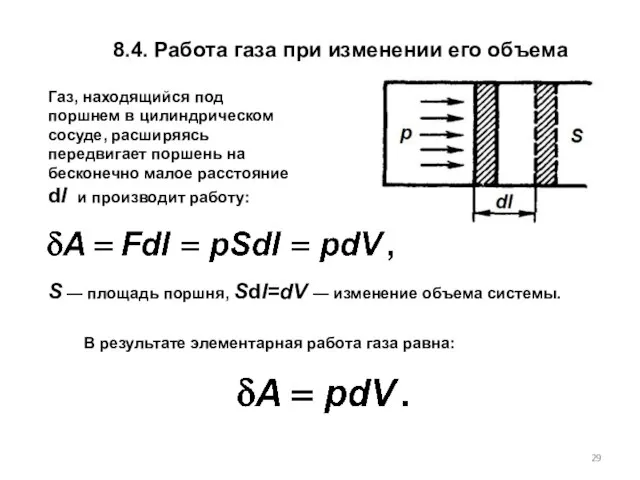
8.4. Работа газа при изменении его объема
Газ, находящийся под поршнем в цилиндрическом сосуде, расширяясь передвигает поршень на бесконечно малое расстояние dl и производит работу:
S — площадь поршня, Sdl=dV — изменение объема системы.
В результате элементарная работа газа равна:

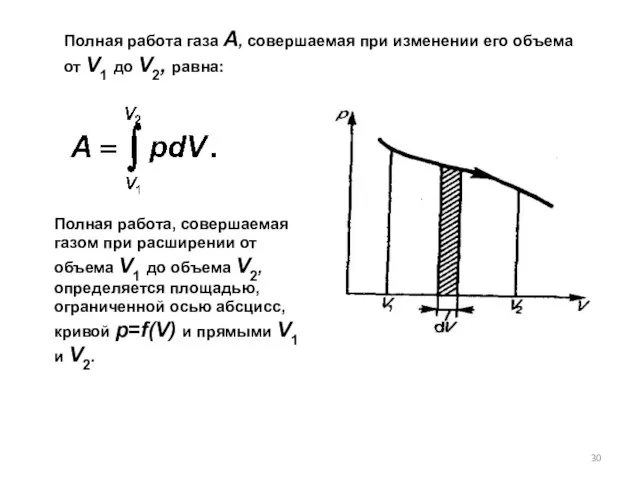
Полная работа газа А, совершаемая при изменении его объема от V1 до V2, равна:
Полная работа, совершаемая газом при расшире­нии от объема V1 до объема V2, определяется площадью, ограниченной осью абсцисс, кривой p=f(V) и прямыми V1 и V2.

8.5. Теплоемкость
Удельная теплоемкость вещества — величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К:
Молярная теплоемкость—величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К:
[Дж/(кг ⋅ К)]
— количество вещества.
[Дж/(моль ⋅ К]
Удельная теплоемкость с связана с молярной Сm, соотношением:
М — молярная масса вещества.

Теплоемкости при постоянном объеме и постоянном давлении различны.
Если газ нагревается при постоянном объеме, то работа внешних сил равна нулю и сообщаемая газу извне теплота идет только на увеличение его внутренней энергии:
Молярная теплоемкость газа при постоянном объеме СV равна изменению внутренней энергии 1 моль газа при повышении его температуры на 1 К.
Если:
то:

Если газ нагревается при постоянном давлении, то:
— уравнение Майера.
Дифференцируя уравнение Клапейрона — Менделеева pVm=RT по T (p=const), получим:
Оно показывает, что Ср всегда больше СV на величину молярной газовой постоянной.

Это объясняется тем, что при нагревании газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа.
Теплоемкость при постоянном давлении можно записать в виде:
При рассмотрении термодинамических процессов важную роль играет отношение Сp к СV :
— коэффициент Пуассона.

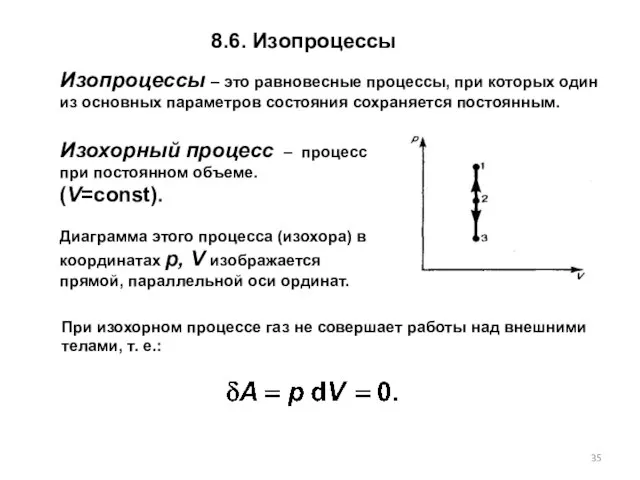
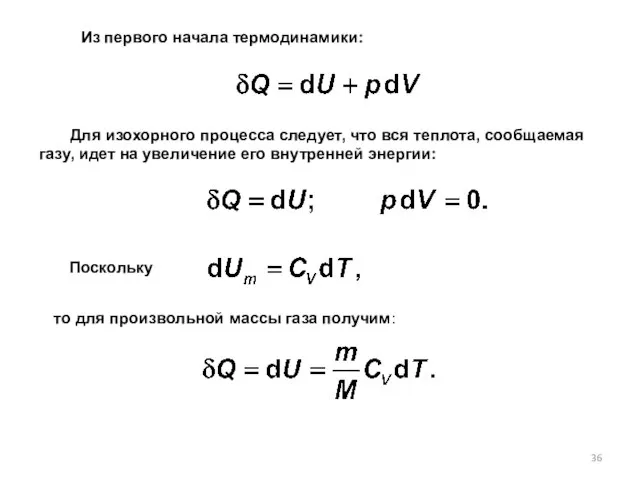
Изопроцессы – это равновесные процессы, при которых один из основных параметров состояния сохраняется постоянным.
Изохорный процесс – процесс при постоянном объеме.
(V=const).
Диаграмма этого процесса (изохора) в координатах р, V изображается прямой, параллельной оси ординат.
При изохорном процессе газ не совершает работы над внешними телами, т. е.:
8.6. Изопроцессы

Для изохорного процесса следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии:
Поскольку
то для произвольной массы газа получим:
Из первого начала термодинамики:

Изобарный процесс – процесс при постоянном давлении
(p=const).
Диаграмма этого процесса (изобара) в координатах р, V изображается прямой, параллельной оси V.
(определяется площадью заштрихованного прямоугольника).
При изобарном процессе работа газа при увеличения объема от V1 до V2 равна:

Если использовать уравнение Клапейрона — Менделеева для выбранных нами двух состояний, то:
откуда:
Тогда выражение для работы изобарного расширения примет вид:

Из предыдущего выражения вытекает физический смысл молярной газовой постоянной R:
«если T2 -T1 =1 К, то для 1 моль газа R=A, т. е. R численно равна работе изобарного расширения 1 моль идеального газа при нагревании его на 1 К».
его внутренняя энергия возрастает на величину:
В изобарном процессе при сообщении газу массой т количества теплоты:

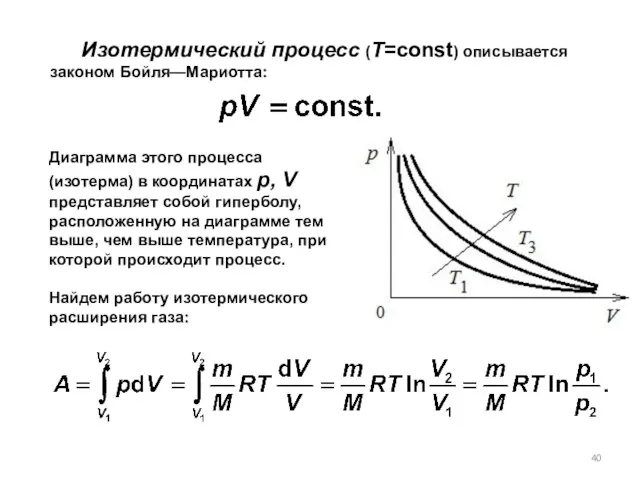
Изотермический процесс (T=const) описывается законом Бойля—Мариотта:
Диаграмма этого процесса (изотерма) в координатах р, V представляет собой гиперболу, расположенную на диаграмме тем выше, чем выше температура, при которой происходит процесс.
Найдем работу изотермического расширения газа:

Так как при Т= const внутренняя энергия идеального газа не изменяется:
то из первого начала термодинамики (δQ=dU+δA) следует, что для изотермического процесса:
т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:

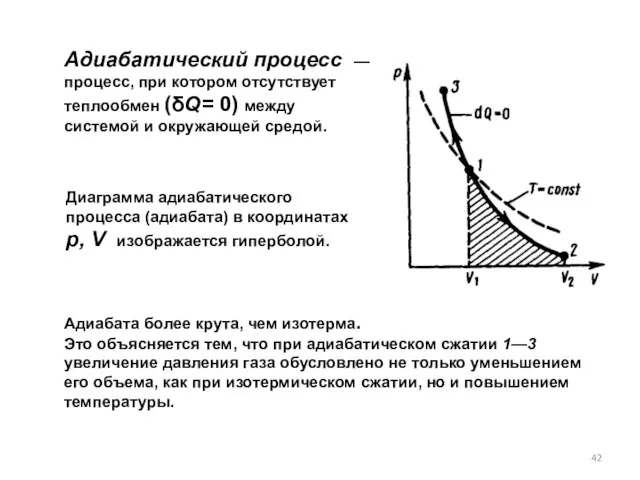
Адиабатический процесс — процесс, при котором отсутствует теплообмен (δQ= 0) между системой и окружающей средой.
Диаграмма адиабатического процесса (адиабата) в координатах р, V изображается гиперболой.
Адиабата более крута, чем изотерма.
Это объясняется тем, что при адиабатическом сжатии 1—3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры.

Из первого начала термодинамики (δQ=dU+δA) для адиабатического процесса следует, что:
т. е. внешняя работа совершается за счет изменения внутренней энергии системы.
тогда:
8.7. Уравнение адиабатического процесса (уравнение Пуассона)

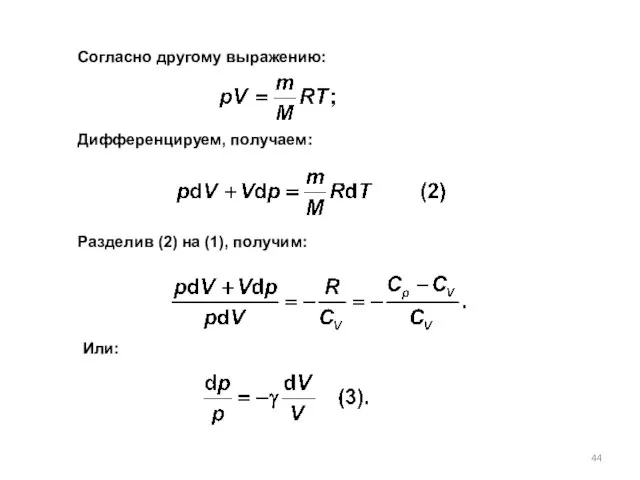
Разделив (2) на (1), получим:
Согласно другому выражению:
Дифференцируем, получаем:
Или:

Интегрируя уравнение (3), получим:
уравнение адиабатического процесса, уравнение Пуассона.
Переходя к переменным Т, V или p с помощью уравнения Клапейрона
получим другие выражения адиабатического процесса:

Рассмотренные процессы происходят при постоянной теплоемкости.
В изобарном и изохорном процессах теплоемкости соответственно равны СV и Сp,
В изотермическом процессе (dT= 0) теплоемкость равна ± ∞,
В адиабатическом (δQ =0) теплоемкость равна нулю.
Процесс, в котором теплоемкость остается постоянной, называется политропным.
Исходя из первого начала термодинамики при условии постоянства теплоемкости (C=const) можно вывести уравнение политропы:
n=(С—Сp)/(С—СV)—показатель политропы.